Машинное обучение — показатели производительности

Существуют различные метрики, которые мы можем использовать для оценки производительности алгоритмов ML, классификации, а также алгоритмов регрессии. Мы должны тщательно выбирать метрики для оценки эффективности ОД, потому что —

• То, как производительность алгоритмов ML измеряется и сравнивается, будет полностью зависеть от выбранного вами показателя.

• То, как вы оцениваете важность различных характеристик в результате, будет полностью зависеть от выбранной вами метрики.

То, как производительность алгоритмов ML измеряется и сравнивается, будет полностью зависеть от выбранного вами показателя.

То, как вы оцениваете важность различных характеристик в результате, будет полностью зависеть от выбранной вами метрики.

Метрики производительности для задач классификации

Мы обсуждали классификацию и ее алгоритмы в предыдущих главах. Здесь мы собираемся обсудить различные метрики производительности, которые можно использовать для оценки прогнозов для задач классификации.

Матрица путаницы

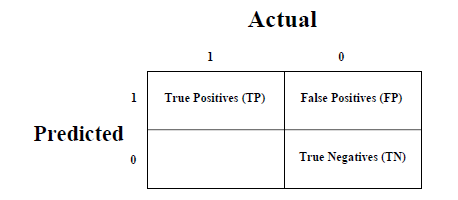
Это самый простой способ измерить производительность задачи классификации, когда выходные данные могут быть двух или более типов классов. Матрица путаницы — это не что иное, как таблица с двумя измерениями, а именно. «Фактические» и «Предсказанные», и, кроме того, оба измерения имеют «Истинные позитивы (TP)», «Истинные негативы (TN)», «Ложные позитивы (FP)», «Ложные негативы (FN)», как показано ниже —

Пояснения терминов, связанных с матрицей путаницы, следующие:

• True Positives (TP) — это тот случай, когда фактический класс и прогнозируемый класс точки данных равны 1.

• True Negatives (TN) — это тот случай, когда фактический класс и прогнозируемый класс точки данных равны 0.

• Ложные срабатывания (FP) — это тот случай, когда фактический класс точки данных равен 0, а прогнозируемый класс точки данных равен 1.

• False Negatives (FN) — это тот случай, когда фактический класс точки данных равен 1, а прогнозируемый класс точки данных равен 0.

True Positives (TP) — это тот случай, когда фактический класс и прогнозируемый класс точки данных равны 1.

True Negatives (TN) — это тот случай, когда фактический класс и прогнозируемый класс точки данных равны 0.

Ложные срабатывания (FP) — это тот случай, когда фактический класс точки данных равен 0, а прогнозируемый класс точки данных равен 1.

False Negatives (FN) — это тот случай, когда фактический класс точки данных равен 1, а прогнозируемый класс точки данных равен 0.

Мы можем использовать функцию confusion_matrix в sklearn.metrics для вычисления Confusion Matrix нашей модели классификации.

Точность классификации

Это наиболее распространенная метрика производительности для алгоритмов классификации. Это может быть определено как число правильных прогнозов, сделанных как отношение всех сделанных прогнозов. Мы можем легко рассчитать его по матрице путаницы с помощью следующей формулы —

Точность= гидроразрываTP+TNTP+FP+FN+TN $$Точность \: = \: \ гидроразрыва {TP + TN} {TP + FP + FN + TN}$$

Мы можем использовать функцию precision_score sklearn.metrics, чтобы вычислить точность нашей модели классификации.

Классификационный отчет

Этот отчет состоит из оценок Точности, Напомним, F1 и Поддержки. Они объясняются следующим образом —

точность

Точность, используемая при поиске документов, может быть определена как количество правильных документов, возвращаемых нашей моделью ML. Мы можем легко рассчитать его по матрице путаницы с помощью следующей формулы —

Точность= гидроразрываTPTP+FN $$Точность \: = \: \ гидроразрыва {TP} {TP + FN}$$

Напомним или Чувствительность

Отзыв может быть определен как число положительных результатов, возвращаемых нашей моделью ML. Мы можем легко вычислить его по матрице смешения с помощью следующей формулы.

Напомним= гидроразрываTPTP+FN $$Напомним \: = \: \ гидроразрыва {TP} {TP + FN}$$

специфичность

Специфичность, в отличие от напоминания, может быть определена как количество негативов, возвращаемых нашей моделью ML. Мы можем легко рассчитать его по матрице путаницы с помощью следующей формулы —

Специфичность= гидроразрываTNTN+FP $$Специфичность \: = \: \ гидроразрыва {TN} {TN + FP}$$

Служба поддержки

Поддержка может быть определена как количество выборок истинного ответа, который лежит в каждом классе целевых значений.

Счет F1

Эта оценка даст нам гармоничное среднее точность и отзыв. Математически, оценка F1 — средневзвешенное значение точности и отзыва. Наилучшее значение F1 будет равно 1, а худшее — 0. Мы можем рассчитать показатель F1 с помощью следующей формулы:

F1=2∗(точность∗вызов)/(точность+отзыв) $$F1 \: \: = \: 2 * (точность * вызов) / (точность + отзыв)$$

Счет F1 имеет равный относительный вклад точности и отзыва.

Мы можем использовать функциюification_report в sklearn.metrics, чтобы получить отчет о классификации нашей модели классификации.

AUC (площадь под кривой ROC)

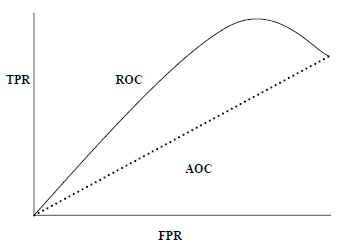
AUC (область под кривой) -ROC (рабочая характеристика приемника) — это показатель производительности, основанный на различных пороговых значениях, для задач классификации. Как следует из названия, ROC — это кривая вероятности, а AUC измеряет отделимость. Проще говоря, метрика AUC-ROC расскажет нам о способности модели различать классы. Чем выше AUC, тем лучше модель.

Математически это может быть создано путем построения графика TPR (True Positive Rate), т. Е. Чувствительности или отзыва по сравнению с FPR (False Positive Rate), т.е. 1-специфичность, при различных пороговых значениях. Ниже приведен график, показывающий ROC, AUC, имеющий TPR на оси Y и FPR на оси X —

Мы можем использовать функцию roc_auc_score sklearn.metrics для вычисления AUC-ROC.

LOGLOSS (логарифмическая потеря)

Это также называется потерей логистической регрессии или потерей перекрестной энтропии. Он в основном определяется по оценкам вероятности и измеряет эффективность модели классификации, где входными данными является значение вероятности в диапазоне от 0 до 1. Это можно понять более четко, дифференцируя его с точностью. Поскольку мы знаем, что точность — это количество прогнозов (прогнозируемое значение = фактическое значение) в нашей модели, тогда как Log Loss — это количество неопределенности нашего прогноза, основанное на том, насколько оно отличается от фактической метки. С помощью значения Log Loss мы можем получить более точное представление о производительности нашей модели. Мы можем использовать функцию log_loss sklearn.metrics, чтобы вычислить Log Loss.

пример

Ниже приведен простой рецепт в Python, который даст нам представление о том, как мы можем использовать вышеописанные метрики производительности в бинарной модели классификации.

from sklearn.metrics import confusion_matrix
from sklearn.metrics import accuracy_score
from sklearn.metrics import classification_report
from sklearn.metrics import roc_auc_score
from sklearn.metrics import log_loss
X_actual = [1, 1, 0, 1, 0, 0, 1, 0, 0, 0]
Y_predic = [1, 0, 1, 1, 1, 0, 1, 1, 0, 0]
results = confusion_matrix(X_actual, Y_predic)
print ('Confusion Matrix :')
print(results)
print ('Accuracy Score is',accuracy_score(X_actual, Y_predic))
print ('Classification Report : ')
print (classification_report(X_actual, Y_predic))
print('AUC-ROC:',roc_auc_score(X_actual, Y_predic))
print('LOGLOSS Value is',log_loss(X_actual, Y_predic))

Выход

Confusion Matrix :
[[3 3]
[1 3]]
Accuracy Score is 0.6
Classification Report :
               precision   recall   f1-score   support
           0        0.75     0.50       0.60         6
           1        0.50     0.75       0.60         4
   micro avg        0.60     0.60       0.60        10
   macro avg        0.62     0.62       0.60        10
weighted avg        0.65     0.60       0.60        10
AUC-ROC: 0.625
LOGLOSS Value is 13.815750437193334

Метрики производительности для задач регрессии

Мы обсуждали регрессию и ее алгоритмы в предыдущих главах. Здесь мы собираемся обсудить различные показатели производительности, которые можно использовать для оценки прогнозов для проблем регрессии.

Средняя абсолютная ошибка (MAE)

Это самый простой показатель ошибки, используемый в задачах регрессии. Это в основном сумма среднего абсолютной разницы между прогнозируемыми и фактическими значениями. Проще говоря, с помощью MAE мы можем получить представление о том, насколько неправильными были прогнозы. MAE не указывает направление модели, то есть не указывает на недостаточную или недостаточную производительность модели. Ниже приведена формула для расчета MAE —

MAE= frac1n sum midY− hatY mid $$MAE \: = \: \ frac {1} {n} \ sum \ mid Y- \ hat {Y} \ mid$$

Здесь y = фактические выходные значения

И $\ hat {Y}$ = прогнозируемые выходные значения.

Мы можем использовать функцию mean_absolute_error в sklearn.metrics для вычисления MAE.

Среднеквадратичная ошибка (MSE)

MSE похож на MAE, но единственное отличие состоит в том, что он возводит в квадрат разницу фактических и прогнозируемых выходных значений перед суммированием их всех вместо использования абсолютного значения. Разницу можно заметить в следующем уравнении —

СКО= гидроразрыва1N сумма(Y− шлемY) $$СКО \: = \: \ гидроразрыва {1} {N} \ сумма (Y- \ шлем {Y})$$

Здесь Y = фактические выходные значения

И $\ hat {Y}$ = прогнозируемые выходные значения.

Мы можем использовать функцию mean_squared_error в sklearn.metrics для вычисления MSE.

R в квадрате (R ² )

R Квадратная метрика обычно используется для пояснительных целей и обеспечивает индикацию достоверности или соответствия набора прогнозируемых выходных значений фактическим выходным значениям. Следующая формула поможет нам понять это —

R2=1− frac frac1n sumni=1(Yi− hatYi)2 frac1n sumni=1(Yi− hatYi)2 $$R ^ {2} \: = \: 1- \ frac {\ frac {1} {n} \ sum_ {i = 1} ^ n (Y_ {i} - \ hat {Y} _ {i}) ^ 2} {{\ frac {1} {n} \ sum_ {i = 1} ^ n (Y_ {i} - \ hat {Y} _ {i}) ^ 2}}$$

В приведенном выше уравнении числитель — это MSE, а знаменатель — это дисперсия значений Y.

Мы можем использовать функцию r2_score sklearn.metrics для вычисления значения R в квадрате.

пример

Ниже приведен простой рецепт в Python, который даст нам представление о том, как мы можем использовать вышеописанные метрики производительности в регрессионной модели: