Алгоритм K-ближайших соседей (KNN) — это тип управляемого алгоритма ML, который может использоваться как для классификации, так и для задач прогнозирования регрессии. Тем не менее, он в основном используется для классификации прогнозирующих проблем в промышленности. Следующие два свойства будут определять KNN хорошо —
-
Алгоритм ленивого обучения — KNN — это алгоритм ленивого обучения, потому что он не имеет специальной фазы обучения и использует все данные для обучения во время классификации.
-
Непараметрический алгоритм обучения — KNN также является непараметрическим алгоритмом обучения, потому что он не предполагает ничего о базовых данных.
Алгоритм ленивого обучения — KNN — это алгоритм ленивого обучения, потому что он не имеет специальной фазы обучения и использует все данные для обучения во время классификации.
Непараметрический алгоритм обучения — KNN также является непараметрическим алгоритмом обучения, потому что он не предполагает ничего о базовых данных.
Работа алгоритма КНН
Алгоритм K-ближайших соседей (KNN) использует «сходство признаков» для прогнозирования значений новых точек данных, что также означает, что новой точке данных будет присвоено значение на основе того, насколько близко он соответствует точкам в обучающем наборе. Мы можем понять его работу с помощью следующих шагов —
Шаг 1 — Для реализации любого алгоритма нам нужен набор данных. Таким образом, во время первого шага KNN мы должны загрузить данные обучения, а также данные испытаний.
Шаг 2 — Далее нам нужно выбрать значение K, то есть ближайшие точки данных. K может быть любым целым числом.
Шаг 3 — Для каждой точки в тестовых данных сделайте следующее —
-
3.1 — Рассчитайте расстояние между данными испытаний и каждой строкой данных тренировки с помощью любого из методов, а именно: Евклидово, Манхэттенское или Хэмминговское расстояние. Наиболее часто используемый метод расчета расстояния — евклидов.
-
3.2 — Теперь, основываясь на значении расстояния, отсортируйте их в порядке возрастания.
-
3.3 — Далее он выберет верхние K строк из отсортированного массива.
-
3.4 — Теперь он назначит класс контрольной точке на основе наиболее часто встречающегося класса этих строк.
3.1 — Рассчитайте расстояние между данными испытаний и каждой строкой данных тренировки с помощью любого из методов, а именно: Евклидово, Манхэттенское или Хэмминговское расстояние. Наиболее часто используемый метод расчета расстояния — евклидов.
3.2 — Теперь, основываясь на значении расстояния, отсортируйте их в порядке возрастания.
3.3 — Далее он выберет верхние K строк из отсортированного массива.
3.4 — Теперь он назначит класс контрольной точке на основе наиболее часто встречающегося класса этих строк.
Шаг 4 — Конец
пример
Ниже приведен пример для понимания концепции K и работы алгоритма KNN.
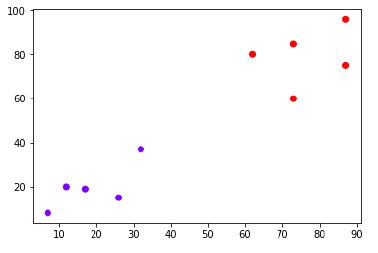
Предположим, у нас есть набор данных, который можно построить следующим образом:
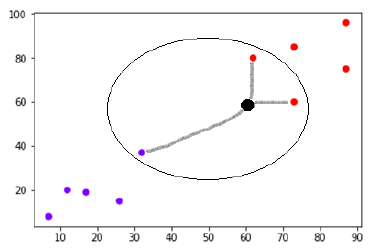
Теперь нам нужно классифицировать новую точку данных с черной точкой (в точке 60, 60) в синий или красный класс. Мы предполагаем, что K = 3, то есть он найдет три ближайшие точки данных. Это показано на следующей диаграмме —
На приведенной выше диаграмме мы видим трех ближайших соседей точки данных с черной точкой. Среди этих трех два из них принадлежат к Красному классу, поэтому черная точка также будет назначена в Красном классе.
Реализация в Python
Как мы знаем, алгоритм K-ближайших соседей (KNN) может использоваться как для классификации, так и для регрессии. Ниже приведены рецепты использования Python в качестве классификатора и регрессора в Python:
КНН как классификатор
Во-первых, начните с импорта необходимых пакетов Python —
import numpy as np import matplotlib.pyplot as plt import pandas as pd
Затем загрузите набор данных iris с веб-ссылки следующим образом:
path = "https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data"
Далее нам нужно назначить имена столбцов для набора данных следующим образом:
headernames = ['sepal-length', 'sepal-width', 'petal-length', 'petal-width', 'Class']
Теперь нам нужно прочитать набор данных в pandas dataframe следующим образом:
dataset = pd.read_csv(path, names = headernames) dataset.head()
| чашелистник длины | чашелистник ширины | Лепесток длина | Лепесток ширины | Учебный класс | |
|---|---|---|---|---|---|
| 0 | 5,1 | 3,5 | 1.4 | 0.2 | Iris-setosa |
| 1 | 4,9 | 3.0 | 1.4 | 0.2 | Iris-setosa |
| 2 | 4,7 | 3,2 | 1,3 | 0.2 | Iris-setosa |
| 3 | 4,6 | 3,1 | 1,5 | 0.2 | Iris-setosa |
| 4 | 5.0 | 3,6 | 1.4 | 0.2 | Iris-setosa |
Предварительная обработка данных будет выполняться с помощью следующих строк сценария.
X = dataset.iloc[:, :-1].values y = dataset.iloc[:, 4].values
Далее, мы разделим данные на разделение на поезда и тесты. Следующий код разделит набор данных на 60% данных обучения и 40% данных тестирования —
from sklearn.model_selection import train_test_split X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.40)
Далее, масштабирование данных будет сделано следующим образом —
from sklearn.preprocessing import StandardScaler scaler = StandardScaler() scaler.fit(X_train) X_train = scaler.transform(X_train) X_test = scaler.transform(X_test)
Далее обучаем модель с помощью класса sklearn класса KNeighborsClassifier следующим образом —
from sklearn.neighbors import KNeighborsClassifier classifier = KNeighborsClassifier(n_neighbors = 8) classifier.fit(X_train, y_train)
Наконец нам нужно сделать прогноз. Это можно сделать с помощью следующего скрипта —
y_pred = classifier.predict(X_test)
Затем распечатайте результаты следующим образом —
from sklearn.metrics import classification_report, confusion_matrix, accuracy_score result = confusion_matrix(y_test, y_pred) print("Confusion Matrix:") print(result) result1 = classification_report(y_test, y_pred) print("Classification Report:",) print (result1) result2 = accuracy_score(y_test,y_pred) print("Accuracy:",result2)
Выход
Confusion Matrix:
[[21 0 0]
[ 0 16 0]
[ 0 7 16]]
Classification Report:
precision recall f1-score support
Iris-setosa 1.00 1.00 1.00 21
Iris-versicolor 0.70 1.00 0.82 16
Iris-virginica 1.00 0.70 0.82 23
micro avg 0.88 0.88 0.88 60
macro avg 0.90 0.90 0.88 60
weighted avg 0.92 0.88 0.88 60
Accuracy: 0.8833333333333333
КНН в качестве регрессора
Во-первых, начните с импорта необходимых пакетов Python —
import numpy as np import pandas as pd
Затем загрузите набор данных iris с веб-ссылки следующим образом:
path = "https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data"
Далее нам нужно назначить имена столбцов для набора данных следующим образом:
headernames = ['sepal-length', 'sepal-width', 'petal-length', 'petal-width', 'Class']
Теперь нам нужно прочитать набор данных в pandas dataframe следующим образом:
data = pd.read_csv(url, names = headernames) array = data.values X = array[:,:2] Y = array[:,2] data.shape output🙁150, 5)
Затем импортируйте KNeighborsRegressor из sklearn, чтобы соответствовать модели —
from sklearn.neighbors import KNeighborsRegressor knnr = KNeighborsRegressor(n_neighbors = 10) knnr.fit(X, y)
Наконец, мы можем найти MSE следующим образом —
print ("The MSE is:",format(np.power(y-knnr.predict(X),2).mean()))
Выход
The MSE is: 0.12226666666666669
Плюсы и минусы КНН
Pros
-
Это очень простой алгоритм для понимания и интерпретации.
-
Это очень полезно для нелинейных данных, потому что в этом алгоритме нет предположения о данных.
-
Это универсальный алгоритм, поскольку мы можем использовать его как для классификации, так и для регрессии.
-
Он имеет относительно высокую точность, но есть гораздо лучшие контролируемые модели обучения, чем KNN.
Это очень простой алгоритм для понимания и интерпретации.
Это очень полезно для нелинейных данных, потому что в этом алгоритме нет предположения о данных.
Это универсальный алгоритм, поскольку мы можем использовать его как для классификации, так и для регрессии.
Он имеет относительно высокую точность, но есть гораздо лучшие контролируемые модели обучения, чем KNN.
Cons
-
Это вычислительно немного дорогой алгоритм, потому что он хранит все данные обучения.
-
Требуется большой объем памяти по сравнению с другими контролируемыми алгоритмами обучения.
-
Прогнозирование медленное в случае большого N.
-
Он очень чувствителен к масштабу данных, а также к несущественным функциям.
Это вычислительно немного дорогой алгоритм, потому что он хранит все данные обучения.
Требуется большой объем памяти по сравнению с другими контролируемыми алгоритмами обучения.
Прогнозирование медленное в случае большого N.
Он очень чувствителен к масштабу данных, а также к несущественным функциям.
Применение КНН
Ниже приведены некоторые из областей, в которых KNN может быть успешно применен:
Банковская система
KNN может использоваться в банковской системе, чтобы предсказать, подходит ли человек для утверждения кредита? Есть ли у этого человека характеристики, аналогичные неплательщикам?
Расчет кредитных рейтингов
Алгоритмы KNN могут быть использованы для определения кредитного рейтинга человека по сравнению с людьми, имеющими сходные черты.
Политика
С помощью алгоритмов KNN мы можем классифицировать потенциального избирателя по разным классам, таким как «Буду голосовать», «Не буду голосовать», «Буду голосовать за партию« Конгресс »,« Буду голосовать за партию «BJP».
Другими областями, в которых может использоваться алгоритм KNN, являются распознавание речи, обнаружение почерка, распознавание изображений и распознавание видео.