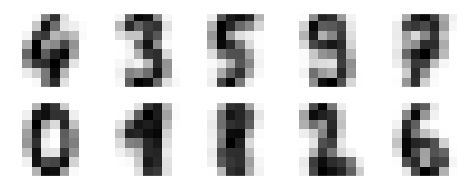ML — Алгоритм кластеризации K-средних

Алгоритм кластеризации K-средних вычисляет центроиды и выполняет итерации, пока мы не найдем оптимальный центроид. Предполагается, что количество кластеров уже известно. Это также называется алгоритм плоской кластеризации . Количество кластеров, идентифицированных по данным алгоритмом, обозначается буквой «K» в K-средних.

В этом алгоритме точки данных назначаются кластеру таким образом, чтобы сумма квадратов расстояния между точками данных и центроидом была бы минимальной. Следует понимать, что меньшее отклонение в кластерах приведет к большему количеству сходных точек данных в одном кластере.

Работа алгоритма K-средних

Мы можем понять работу алгоритма кластеризации K-Means с помощью следующих шагов:

Шаг 1 — Во-первых, нам нужно указать количество кластеров, K, которые должны быть сгенерированы этим алгоритмом.

Шаг 2 — Затем случайным образом выберите K точек данных и назначьте каждую точку данных кластеру. Проще говоря, классифицировать данные на основе количества точек данных.

Шаг 3 — Теперь он будет вычислять кластерные центроиды.

Шаг 4 — Далее, продолжайте повторять следующее до тех пор, пока мы не найдем оптимальный центроид, который является назначением точек данных кластерам, которые больше не меняются

• 4.1 — Сначала будет вычислена сумма квадратов расстояния между точками данных и центроидами.

• 4.2 — Теперь мы должны назначить каждую точку данных кластеру, который находится ближе, чем другой кластер (центроид).

• 4.3 — Наконец, вычислите центроиды для кластеров, взяв среднее значение всех точек данных этого кластера.

4.1 — Сначала будет вычислена сумма квадратов расстояния между точками данных и центроидами.

4.2 — Теперь мы должны назначить каждую точку данных кластеру, который находится ближе, чем другой кластер (центроид).

4.3 — Наконец, вычислите центроиды для кластеров, взяв среднее значение всех точек данных этого кластера.

K-означает следовать подходу ожидания-максимизации для решения проблемы. Шаг ожидания используется для назначения точек данных ближайшему кластеру, а шаг максимизации используется для вычисления центроида каждого кластера.

При работе с алгоритмом K-means мы должны позаботиться о следующих вещах:

• При работе с алгоритмами кластеризации, включая K-Means, рекомендуется стандартизировать данные, поскольку такие алгоритмы используют измерения на основе расстояний для определения сходства между точками данных.

• Из-за итеративной природы K-средних и случайной инициализации центроидов K-средние могут придерживаться локального оптимума и могут не сходиться к глобальному оптимуму. Вот почему рекомендуется использовать разные инициализации центроидов.

При работе с алгоритмами кластеризации, включая K-Means, рекомендуется стандартизировать данные, поскольку такие алгоритмы используют измерения на основе расстояний для определения сходства между точками данных.

Из-за итеративной природы K-средних и случайной инициализации центроидов K-средние могут придерживаться локального оптимума и могут не сходиться к глобальному оптимуму. Вот почему рекомендуется использовать разные инициализации центроидов.

Реализация в Python

Следующие два примера реализации алгоритма кластеризации K-Means помогут нам в его лучшем понимании:

Пример 1

Это простой пример, чтобы понять, как работает k-means. В этом примере мы сначала сгенерируем 2D-набор данных, содержащий 4 разных больших объекта, а затем применим алгоритм k-средних, чтобы увидеть результат.

Сначала мы начнем с импорта необходимых пакетов —

%matplotlib inline
import matplotlib.pyplot as plt
import seaborn as sns; sns.set()
import numpy as np
from sklearn.cluster import KMeans

Следующий код сгенерирует 2D, содержащий четыре капли:

from sklearn.datasets.samples_generator import make_blobs
X, y_true = make_blobs(n_samples = 400, centers = 4, cluster_std = 0.60, random_state = 0)

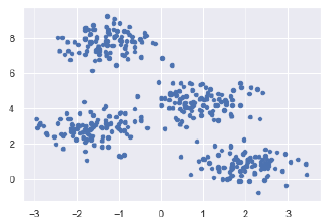
Далее, следующий код поможет нам визуализировать набор данных —

plt.scatter(X[:, 0], X[:, 1], s = 20);
plt.show()

Затем создайте объект KMeans вместе с указанием количества кластеров, обучите модель и сделайте прогноз следующим образом:

kmeans = KMeans(n_clusters = 4)
kmeans.fit(X)
y_kmeans = kmeans.predict(X)

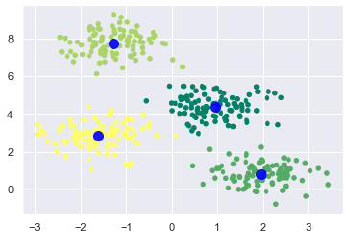
Теперь с помощью следующего кода мы можем построить и визуализировать центры кластера, выбранные с помощью k-средних оценки Python —

from sklearn.datasets.samples_generator import make_blobs
X, y_true = make_blobs(n_samples = 400, centers = 4, cluster_std = 0.60, random_state = 0)

Далее, следующий код поможет нам визуализировать набор данных —

plt.scatter(X[:, 0], X[:, 1], c = y_kmeans, s = 20, cmap = 'summer')
centers = kmeans.cluster_centers_
plt.scatter(centers[:, 0], centers[:, 1], c = 'blue', s = 100, alpha = 0.9);
plt.show()

Пример 2

Давайте перейдем к другому примеру, в котором мы собираемся применить кластеризацию K-средних к набору простых цифр. K-means попытается идентифицировать похожие цифры, не используя информацию оригинальной этикетки.

Сначала мы начнем с импорта необходимых пакетов —

%matplotlib inline
import matplotlib.pyplot as plt
import seaborn as sns; sns.set()
import numpy as np
from sklearn.cluster import KMeans

Затем загрузите набор цифр из sklearn и создайте из него объект. Мы также можем найти количество строк и столбцов в этом наборе данных следующим образом:

from sklearn.datasets import load_digits
digits = load_digits()
digits.data.shape

Выход

(1797, 64)

Приведенный выше вывод показывает, что этот набор данных имеет 1797 выборок с 64 признаками.

Мы можем выполнить кластеризацию, как в примере 1 выше —

kmeans = KMeans(n_clusters = 10, random_state = 0)
clusters = kmeans.fit_predict(digits.data)
kmeans.cluster_centers_.shape

Выход

(10, 64)

Приведенный выше вывод показывает, что K-means создал 10 кластеров с 64 функциями.

fig, ax = plt.subplots(2, 5, figsize=(8, 3))
centers = kmeans.cluster_centers_.reshape(10, 8, 8)
for axi, center in zip(ax.flat, centers):
axi.set(xticks=[], yticks=[])
axi.imshow(center, interpolation='nearest', cmap=plt.cm.binary)

Выход

В качестве результата мы получим следующее изображение, показывающее центры кластеров, изученные с помощью k-средних.

Следующие строки кода будут сопоставлять изученные метки кластера с истинными метками, найденными в них:

from scipy.stats import mode
labels = np.zeros_like(clusters)
for i in range(10):
   mask = (clusters == i)
   labels[mask] = mode(digits.target[mask])[0]

Далее мы можем проверить точность следующим образом:

from sklearn.metrics import accuracy_score
accuracy_score(digits.target, labels)

Выход

0.7935447968836951

Приведенный выше вывод показывает, что точность составляет около 80%.

Преимущества и недостатки

преимущества

Ниже приведены некоторые преимущества алгоритмов кластеризации K-Means:

• Это очень легко понять и реализовать.

• Если у нас будет большое количество переменных, тогда K-means будет быстрее, чем иерархическая кластеризация.

• При повторном вычислении центроидов экземпляр может изменить кластер.

• Более плотные кластеры формируются с помощью K-средних по сравнению с иерархической кластеризацией.

Это очень легко понять и реализовать.

Если у нас будет большое количество переменных, тогда K-means будет быстрее, чем иерархическая кластеризация.

При повторном вычислении центроидов экземпляр может изменить кластер.

Более плотные кластеры формируются с помощью K-средних по сравнению с иерархической кластеризацией.

Недостатки

Ниже приведены некоторые недостатки алгоритмов кластеризации K-Means:

• Немного сложно предсказать количество кластеров, то есть значение k.

• На выход сильно влияют исходные данные, такие как количество кластеров (значение k)

• Порядок данных будет иметь сильное влияние на конечный результат.

• Это очень чувствительно к масштабированию. Если мы будем масштабировать наши данные с помощью нормализации или стандартизации, то вывод полностью изменится.

• В кластеризации плохо работать, если кластеры имеют сложную геометрическую форму.

Немного сложно предсказать количество кластеров, то есть значение k.

На выход сильно влияют исходные данные, такие как количество кластеров (значение k)

Порядок данных будет иметь сильное влияние на конечный результат.

Это очень чувствительно к масштабированию. Если мы будем масштабировать наши данные с помощью нормализации или стандартизации, то вывод полностью изменится.

В кластеризации плохо работать, если кластеры имеют сложную геометрическую форму.

Применение алгоритма кластеризации K-средних

Основными целями кластерного анализа являются —

• Чтобы получить значимую интуицию от данных, с которыми мы работаем.

• Cluster-then-предсказывать, где будут построены разные модели для разных подгрупп.

Чтобы получить значимую интуицию от данных, с которыми мы работаем.

Cluster-then-предсказывать, где будут построены разные модели для разных подгрупп.

Для достижения вышеупомянутых целей кластеризация K-средних достаточно эффективна. Может использоваться в следующих приложениях —