ML — Машина опорных векторов (SVM)

Машины опорных векторов (SVM) — это мощные, но гибкие алгоритмы машинного обучения под наблюдением, которые используются как для классификации, так и для регрессии. Но, как правило, они используются в задачах классификации. В 1960-х годах SVM были впервые представлены, но позже они были усовершенствованы в 1990 году. SVM имеют свой уникальный способ реализации по сравнению с другими алгоритмами машинного обучения. В последнее время они чрезвычайно популярны из-за их способности обрабатывать несколько непрерывных и категориальных переменных.

Работа СВМ

Модель SVM — это в основном представление разных классов на гиперплоскости в многомерном пространстве. Гиперплоскость будет сгенерирована SVM итеративным способом, так что ошибка может быть минимизирована. Цель SVM — разделить наборы данных на классы, чтобы найти максимальную предельную гиперплоскость (MMH).

Следующие важные понятия в SVM —

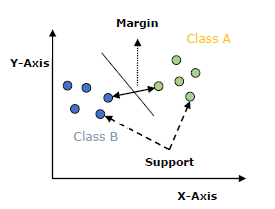
• Векторы поддержки — Точки данных, которые находятся ближе всего к гиперплоскости, называются векторами поддержки. Разделительная линия будет определяться с помощью этих точек данных.

• Гиперплоскость — как мы видим на приведенной выше диаграмме, это плоскость принятия решений или пространство, которое разделено между набором объектов, имеющих разные классы.

• Маржа — это может быть определено как разрыв между двумя линиями в точках данных шкафа разных классов. Его можно рассчитать как перпендикулярное расстояние от линии до опорных векторов. Большая маржа считается хорошей маржей, а маленькая маржа считается плохой маржей.

Векторы поддержки — Точки данных, которые находятся ближе всего к гиперплоскости, называются векторами поддержки. Разделительная линия будет определяться с помощью этих точек данных.

Гиперплоскость — как мы видим на приведенной выше диаграмме, это плоскость принятия решений или пространство, которое разделено между набором объектов, имеющих разные классы.

Маржа — это может быть определено как разрыв между двумя линиями в точках данных шкафа разных классов. Его можно рассчитать как перпендикулярное расстояние от линии до опорных векторов. Большая маржа считается хорошей маржей, а маленькая маржа считается плохой маржей.

Основная цель SVM — разделить наборы данных на классы, чтобы найти максимальную предельную гиперплоскость (MMH), и это можно сделать в следующие два шага:

• Во-первых, SVM итеративно генерирует гиперплоскости, которые наилучшим образом разделяют классы.

• Затем он выберет гиперплоскость, которая правильно разделяет классы.

Во-первых, SVM итеративно генерирует гиперплоскости, которые наилучшим образом разделяют классы.

Затем он выберет гиперплоскость, которая правильно разделяет классы.

Реализация SVM в Python

• Для реализации SVM в Python — мы начнем со импорта стандартных библиотек следующим образом —

Для реализации SVM в Python — мы начнем со импорта стандартных библиотек следующим образом —

Ядра SVM

На практике алгоритм SVM реализуется с помощью ядра, которое преобразует пространство входных данных в требуемую форму. SVM использует технику, называемую уловкой ядра, в которой ядро ​​занимает низкоразмерное пространство ввода и преобразует его в пространство более высокого измерения. Проще говоря, ядро ​​преобразует неразделимые задачи в отдельные, добавляя в него больше измерений. Это делает SVM более мощным, гибким и точным. Ниже приведены некоторые из типов ядер, используемых SVM.

Линейное ядро

Его можно использовать как произведение точек между любыми двумя наблюдениями. Формула линейного ядра выглядит следующим образом:

К(х,Xя)=сумма(х∗XI) $$К (х, X_ {я}) \: = \: сумма (х * X_ {I})$$

Из приведенной выше формулы видно, что произведение двух векторов на ? & ?? является суммой умножения каждой пары входных значений.

Полиномиальное Ядро

Это более обобщенная форма линейного ядра и различение искривленного или нелинейного входного пространства. Ниже приведена формула для полиномиального ядра —

к(Х,Х)=1+сумма(Х∗Xг) шапкуd $$к (Х, Х) \: = 1 + сумма (Х * X_ {г}) \ шапку \: d$$

Здесь d — степень полинома, которую мы должны указать вручную в алгоритме обучения.

Ядро радиальной базовой функции (RBF)

Ядро RBF, чаще всего используемое в классификации SVM, отображает входное пространство в неопределенное пространство измерений. Следующая формула объясняет это математически —

K(X,XI)=ехр(−gamma∗сумма(X−XI Шляпа2)) $$K (X, XI) \: = ехр (-gamma ^ * сумма (X-XI \ Шляпа \: 2))$$

Здесь гамма колеблется от 0 до 1. Нам нужно вручную указать это в алгоритме обучения. Хорошее значение гаммы по умолчанию — 0,1.

Поскольку мы реализовали SVM для линейно разделимых данных, мы можем реализовать его в Python для данных, которые не являются линейно разделимыми. Это можно сделать с помощью ядра.

пример

Ниже приведен пример создания классификатора SVM с использованием ядер. Мы будем использовать набор данных iris из scikit-learn —

Мы начнем с импорта следующих пакетов —

import pandas as pd
import numpy as np
from sklearn import svm, datasets
import matplotlib.pyplot as plt

Теперь нам нужно загрузить входные данные —

iris = datasets.load_iris()

Из этого набора данных мы берем первые две особенности следующим образом:

X = iris.data[:, :2]
y = iris.target

Далее мы построим границы SVM с исходными данными следующим образом:

x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
h = (x_max / x_min)/100
xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))
X_plot = np.c_[xx.ravel(), yy.ravel()]

Теперь нам нужно указать значение параметра регуляризации следующим образом:

C = 1.0

Далее, объект классификатора SVM может быть создан следующим образом:

Svc_classifier = svm.SVC (ядро = ‘линейный’, C = C) .fit (X, y)

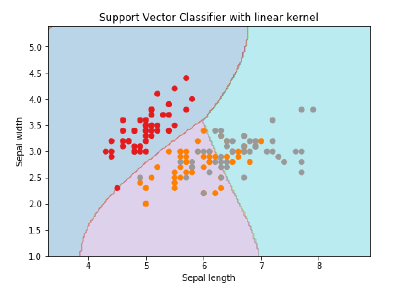
Z = svc_classifier.predict(X_plot)
Z = Z.reshape(xx.shape)
plt.figure(figsize=(15, 5))
plt.subplot(121)
plt.contourf(xx, yy, Z, cmap=plt.cm.tab10, alpha=0.3)
plt.scatter(X[:, 0], X[:, 1], c=y, cmap=plt.cm.Set1)
plt.xlabel('Sepal length')
plt.ylabel('Sepal width')
plt.xlim(xx.min(), xx.max())
plt.title('Support Vector Classifier with linear kernel')

Выход

Text(0.5, 1.0, 'Support Vector Classifier with linear kernel')

Для создания классификатора SVM с ядром rbf мы можем изменить ядро ​​на rbf следующим образом:

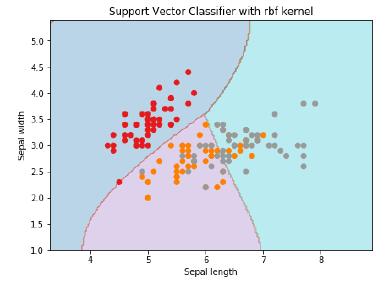
Svc_classifier = svm.SVC(kernel = 'rbf', gamma =‘auto’,C = C).fit(X, y)
Z = svc_classifier.predict(X_plot)
Z = Z.reshape(xx.shape)
plt.figure(figsize=(15, 5))
plt.subplot(121)
plt.contourf(xx, yy, Z, cmap = plt.cm.tab10, alpha = 0.3)
plt.scatter(X[:, 0], X[:, 1], c = y, cmap = plt.cm.Set1)
plt.xlabel('Sepal length')
plt.ylabel('Sepal width')
plt.xlim(xx.min(), xx.max())
plt.title('Support Vector Classifier with rbf kernel')

Выход

Text(0.5, 1.0, 'Support Vector Classifier with rbf kernel')

Мы устанавливаем значение гаммы в ‘auto’, но вы также можете указать его значение от 0 до 1.

Плюсы и минусы классификаторов SVM

Плюсы классификатора SVM

Классификаторы SVM предлагают высокую точность и хорошо работают с пространством большого размера. Классификаторы SVM в основном используют подмножество обучающих точек, следовательно, в результате используется очень меньше памяти.

Минусы SVM классификаторов

Они имеют большое время обучения, поэтому на практике не подходят для больших наборов данных. Другим недостатком является то, что классификаторы SVM плохо работают с перекрывающимися классами.