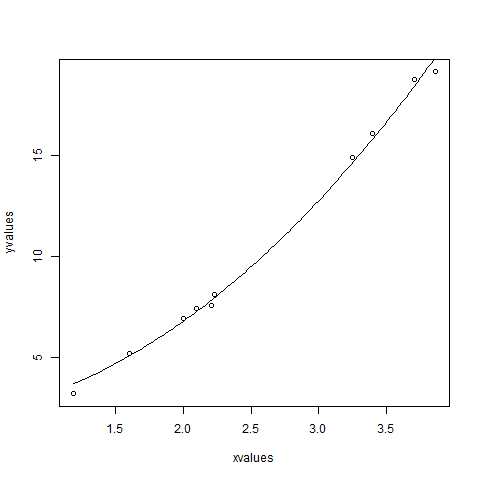R — нелинейная наименьшая площадь

При моделировании данных реального мира для регрессионного анализа мы наблюдаем, что редко случается, что уравнение модели представляет собой линейное уравнение, дающее линейный график. В большинстве случаев уравнение модели данных реального мира включает в себя математические функции более высокой степени, такие как показатель степени 3 или функция sin. В таком случае график модели дает кривую, а не линию. Целью как линейной, так и нелинейной регрессии является настройка значений параметров модели, чтобы найти линию или кривую, которая ближе всего подходит к вашим данным. Найдя эти значения, мы сможем оценить переменную отклика с хорошей точностью.

В регрессии наименьших квадратов мы устанавливаем регрессионную модель, в которой сумма квадратов вертикальных расстояний различных точек от кривой регрессии минимизируется. Обычно мы начинаем с определенной модели и принимаем некоторые значения для коэффициентов. Затем мы применяем функцию nls () для R, чтобы получить более точные значения вместе с доверительными интервалами.

Синтаксис

Основной синтаксис для создания нелинейного критерия наименьших квадратов в R —

nls(formula, data, start)

Ниже приведено описание используемых параметров:

• формула — это формула нелинейной модели, включающая переменные и параметры.

• Данные — это фрейм данных, используемый для оценки переменных в формуле.

• start — именованный список или именованный числовой вектор начальных оценок.

формула — это формула нелинейной модели, включающая переменные и параметры.

Данные — это фрейм данных, используемый для оценки переменных в формуле.

start — именованный список или именованный числовой вектор начальных оценок.

пример

Рассмотрим нелинейную модель с предположением начальных значений ее коэффициентов. Далее мы увидим, каковы доверительные интервалы этих предполагаемых значений, чтобы мы могли судить, насколько хорошо эти значения попадают в модель.

Итак, давайте рассмотрим приведенное ниже уравнение для этой цели —

a = b1*x^2+b2

Давайте предположим, что начальные коэффициенты равны 1 и 3, и поместим эти значения в функцию nls ().

Live Demo

xvalues <- c(1.6,2.1,2,2.23,3.71,3.25,3.4,3.86,1.19,2.21)
yvalues <- c(5.19,7.43,6.94,8.11,18.75,14.88,16.06,19.12,3.21,7.58)

# Give the chart file a name.
png(file = "nls.png")


# Plot these values.
plot(xvalues,yvalues)


# Take the assumed values and fit into the model.
model <- nls(yvalues ~ b1*xvalues^2+b2,start = list(b1 = 1,b2 = 3))

# Plot the chart with new data by fitting it to a prediction from 100 data points.
new.data <- data.frame(xvalues = seq(min(xvalues),max(xvalues),len = 100))
lines(new.data$xvalues,predict(model,newdata = new.data))

# Save the file.
dev.off()

# Get the sum of the squared residuals.
print(sum(resid(model)^2))

# Get the confidence intervals on the chosen values of the coefficients.
print(confint(model))

[1] 1.081935
Waiting for profiling to be done...
       2.5%    97.5%
b1 1.137708 1.253135
b2 1.497364 2.496484