RADAR — это система обнаружения на основе электромагнитного излучения, которая работает, излучая электромагнитные волны, а затем изучая эхо или отраженные обратные волны.
Полной формой RADAR является обнаружение и обнаружение диода RA. Обнаружение относится к тому, присутствует ли цель или нет. Мишень может быть стационарной или подвижной, т.е. нестационарной. Ранжирование относится к расстоянию между радаром и целью.
Радары могут использоваться для различных применений на земле, на море и в космосе. Приложения радаров перечислены ниже.
- Управление воздушным движением
- Безопасность корабля
- Чувство отдаленных мест
- Военные приложения
В любом приложении Радар основной принцип остается тем же. Давайте теперь обсудим принцип радара.
Основной принцип радара
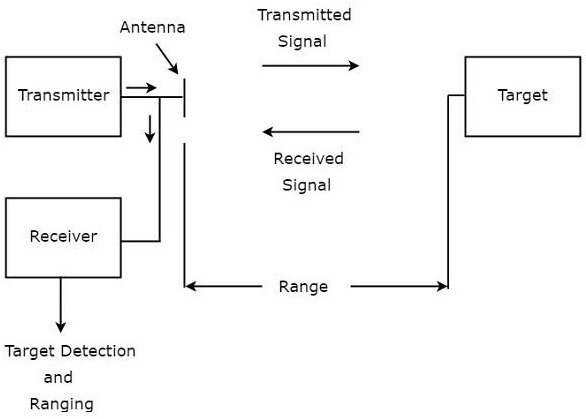
Радар используется для обнаружения объектов и определения их местоположения. Мы можем понять основной принцип радара из следующего рисунка.
Как показано на рисунке, радар в основном состоит из передатчика и приемника. Он использует одну и ту же антенну как для передачи, так и для приема сигналов. Функция передатчика заключается в передаче сигнала радара в направлении присутствующей цели.
Цель отражает этот полученный сигнал в различных направлениях. Сигнал, который отражается обратно к антенне, принимается приемником .
Терминология радиолокационных систем
Ниже приведены основные термины, которые полезны в этом руководстве.
- Спектр
- Частота повторения импульсов
- Максимальный однозначный диапазон
- Минимальный диапазон
Теперь давайте поговорим об этих основных терминах один за другим.
Спектр
Расстояние между радаром и целью называется дальностью цели или просто дальностью R. Мы знаем, что радар передает сигнал к цели и, соответственно, цель посылает эхо-сигнал на радар со скоростью света, C.
Пусть время, необходимое для прохождения сигнала от радара к цели и обратно к радару, будет равно «T». Двустороннее расстояние между радаром и целью будет 2R, поскольку расстояние между радаром и целью составляет R.
Теперь следующая формула для скорости .
$$ Speed = \ frac {Расстояние} {Время} $$
$$ \ Rightarrow Distance = Скорость \ раз Время $$
$$ \ Rightarrow 2R = C \ times T $$
$$ R = \ гидроразрыва {КТ} {2} \: \: \: \: \: Уравнение \: 1 $$
Мы можем найти диапазон цели , подставив значения C & T в уравнение 1.
Частота повторения импульсов
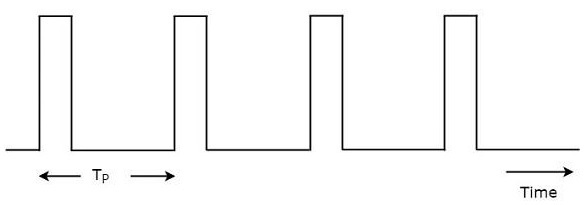
Радарные сигналы должны передаваться при каждом тактовом импульсе. Длительность между двумя тактовыми импульсами должна быть правильно выбрана таким образом, чтобы эхо-сигнал, соответствующий текущему тактовому импульсу, принимался до следующего тактового импульса. Типичная форма волны радара показана на следующем рисунке.
Как показано на рисунке, радар передает периодический сигнал. Он имеет серию узких прямоугольных импульсов. Временной интервал между последовательными тактовыми импульсами называется временем повторения импульсов , $ T_P $.
Обратная величина времени повторения импульса называется частотой повторения импульсов , $ f_P $. Математически это можно представить как
$$ F_p = \ гидроразрыва {1} {T_P} \: \: \: \: \: Уравнение \: 2 $$
Следовательно, частота повторения импульсов — это не что иное, как частота, на которой радар передает сигнал.
Максимальный однозначный диапазон
Мы знаем, что радарные сигналы должны передаваться при каждом тактовом импульсе. Если мы выберем более короткую длительность между двумя тактовыми импульсами, то эхо-сигнал, соответствующий текущему тактовому импульсу, будет получен после следующего тактового импульса. Из-за этого диапазон цели кажется меньше, чем фактический диапазон.
Таким образом, мы должны выбрать длительность между двумя тактовыми импульсами таким образом, чтобы эхо-сигнал, соответствующий текущему тактовому импульсу, был получен до начала следующего тактового импульса. Затем мы получим истинный диапазон цели, который также называется максимальным однозначным диапазоном цели или просто максимальным однозначным диапазоном .
Замените $ R = R_ {un} $ и $ T = T_P $ в уравнении 1.
$$ R_ {ип} = \ гидроразрыва {CT_P} {2} \: \: \: \: \: Уравнение \: 3 $$
Из уравнения 2 мы получим время повторения импульсов, $ T_P $ как обратную частоту повторения импульсов, $ f_P $. Математически это можно представить как
$$ T_P = \ гидроразрыва {1} {F_p} \: \: \: \: \: Уравнение \: 4 $$
Заменить уравнение 4 в уравнении 3.
$$ R_ {un} = \ frac {C \ left (\ frac {1} {f_P} \ right)} {2} $$
$$ R_ {ип} = \ гидроразрыва {C}, {2f_P} \: \: \: \: \: Уравнение \: 5 $$
Мы можем использовать либо Уравнение 3, либо Уравнение 5 для расчета максимального однозначного диапазона цели.
-
Мы получим значение максимального однозначного диапазона цели, $ R_ {un} $, подставив в уравнение 3 значения $ C $ и $ T_P $.
-
Аналогично, мы получим значение максимального однозначного диапазона цели, $ R_ {un} $, подставив в уравнение 5 значения $ C $ и $ f_P $.
Мы получим значение максимального однозначного диапазона цели, $ R_ {un} $, подставив в уравнение 3 значения $ C $ и $ T_P $.
Аналогично, мы получим значение максимального однозначного диапазона цели, $ R_ {un} $, подставив в уравнение 5 значения $ C $ и $ f_P $.
Минимальный диапазон
Мы получим минимальный диапазон цели, если учесть время, необходимое для получения эхо-сигнала на радаре после передачи сигнала с радара, в качестве ширины импульса. Это также называют самым коротким диапазоном цели.
Замените $ R = R_ {min} $ и $ T = \ tau $ в уравнении 1.
$$ R_ {} мин = \ гидроразрыва {С \ тау} {2} \: \: \: \: \: Уравнение \: 6 $$
Мы получим значение минимального диапазона цели, $ R_ {min} $, подставив в уравнение 6 значения $ C $ и $ \ tau $.