Одна антенна может излучать определенное количество энергии в определенном направлении. Очевидно, что количество мощности излучения будет увеличено, когда мы будем использовать группу антенн вместе. Группа антенн называется антенной решеткой .
Антенная решетка — это излучающая система, состоящая из радиаторов и элементов. Каждый из этих излучателей имеет свое индукционное поле. Элементы расположены так близко, что каждый лежит в индукционном поле соседнего. Следовательно, диаграмма излучения, создаваемая ими, будет векторной суммой отдельных.
Антенны излучают индивидуально, и, когда они расположены в массиве, излучение всех элементов суммируется, чтобы сформировать луч излучения, который имеет высокий коэффициент усиления, высокую направленность и лучшую производительность с минимальными потерями.
Антенная решетка называется фазированной антенной решеткой, если форма и направление диаграммы направленности зависит от относительных фаз и амплитуд токов, присутствующих в каждой антенне этой решетки.
Радиационная картина
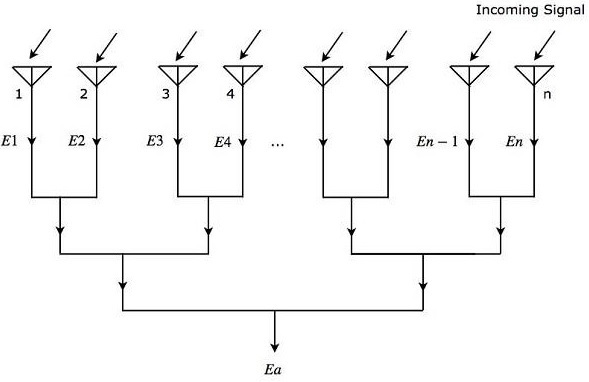
Рассмотрим «n» изотропных элементов излучения, которые при объединении образуют массив . Приведенный ниже рисунок поможет вам понять то же самое. Пусть интервал между последовательными элементами будет единицами ‘d’.
Как показано на рисунке, все излучающие элементы получают одинаковый входящий сигнал. Таким образом, каждый элемент выдает равное выходное напряжение $ sin \ left (\ omega t \ right) $. Однако между последовательными элементами будет одинаковая разность фаз $ \ Psi $. Математически это можно записать как —
$$ \ Psi = \ frac {2 \ pi d \ sin \ theta} {\ lambda} \: \: \: \: \: Equation \: 1 $$
Куда,
$ \ theta $ — это угол, под которым входящий сигнал падает на каждый элемент излучения.
Математически мы можем записать выражения для выходных напряжений ‘n’ элементов излучения индивидуально как
$$ E_1 = \ sin \ left [\ omega t \ right] $$
$$ E_2 = \ sin \ left [\ omega t + \ Psi \ right] $$
$$ E_3 = \ sin \ left [\ omega t + 2 \ Psi \ right] $$
$$ $$.
$$ $$.
$$ $$.
$$ E_n = \ sin \ left [\ omega t + \ left (N-1 \ right) \ Psi \ right] $$
Куда,
$ E_1, E_2, E_3,…, E_n $ — выходные напряжения первого, второго, третьего,…, n- го излучающих элементов соответственно.
$ \ omega $ — угловая частота сигнала.
Мы получим общее выходное напряжение массива $ E_a $ путем сложения выходных напряжений каждого элемента, присутствующего в этом массиве, поскольку все эти излучающие элементы соединены в линейный массив. Математически это можно представить как —
$$ E_a = E_1 + E_2 + E_3 +… + E_n \: \: \: Уравнение \: 2 $$
Подставим значения $ E_1, E_2, E_3,…, E_n $ в уравнение 2.
$$ E_a = \ sin \ left [\ omega t \ right] + \ sin \ left [\ omega t + \ Psi \ right] + \ sin \ left [\ omega t + 2 \ Psi \ right] + \ sin \ left [\ omega t + \ left (n-1 \ right) \ Psi \ right] $$
$$ \ Rightarrow E_a = \ sin \ left [\ omega t + \ frac {(n-1) \ Psi)} {2} \ right] \ frac {\ sin \ left [\ frac {n \ Psi} {2} \ right]} {\ sin \ left [\ frac {\ Psi} {2} \ right]} \: \: \: \: \: Equation \: 3 $$
В уравнении 3 есть два условия. Из первого слагаемого мы можем наблюдать, что общее выходное напряжение $ E_a $ является синусоидальной волной, имеющей угловую частоту $ \ omega $. Но он имеет фазовый сдвиг $ \ left (n − 1 \ right) \ Psi / 2 $. Второе слагаемое в уравнении 3 является амплитудным фактором .
Величина уравнения 3 будет
$$ \ left | E_a \ right | = \ left | \ frac {\ sin \ left [\ frac {n \ Psi} {2} \ right]} {\ sin \ left [\ frac {\ Psi} {2} \ right]} \ right | \: \: \: \: \: Уравнение \: 4 $$
Мы получим следующее уравнение, подставив уравнение 1 в уравнение 4.
$$ \ left | E_a \ right | = \ left | \ frac {\ sin \ left [\ frac {n \ pi d \ sin \ theta} {\ lambda} \ right]} {\ sin \ left [\ frac {\ pi d \ sin \ theta} {\ lambda} \ right]} \ right | \: \: \: \: \: Equation \: 5 $$
Уравнение 5 называется диаграммой напряженности поля . Шаблон напряженности поля будет иметь значения нулей, когда числитель уравнения 5 равен нулю
$$ \ sin \ left [\ frac {n \ pi d \ sin \ theta} {\ lambda} \ right] = 0 $$
$$ \ Rightarrow \ frac {n \ pi d \ sin \ theta} {\ lambda} = \ pm m \ pi $$
$$ \ Rightarrow nd \ sin \ theta = \ pm m \ lambda $$
$$ \ Rightarrow \ sin \ theta = \ pm \ frac {m \ lambda} {nd} $$
Куда,
$ m $ — это целое число, равное 1, 2, 3 и т. д.
Мы можем найти максимальные значения модели напряженности поля, используя правило L-Hospital, когда числитель и знаменатель уравнения 5 равны нулю. Мы можем наблюдать, что если знаменатель уравнения 5 становится равным нулю, то числитель уравнения 5 также становится равным нулю.
Теперь давайте получим условие, при котором знаменатель уравнения 5 становится равным нулю.
$$ \ sin \ left [\ frac {\ pi d \ sin \ theta} {\ lambda} \ right] = 0 $$
$$ \ Rightarrow \ frac {\ pi d \ sin \ theta} {\ lambda} = \ pm p \ pi $$
$$ \ Rightarrow d \ sin \ theta = \ pm p \ lambda $$
$$ \ Rightarrow \ sin \ theta = \ pm \ frac {p \ lambda} {d} $$
Куда,
$ p $ — это целое число, равное 0, 1, 2, 3 и т. д.
Если мы рассмотрим $ p $ как ноль, то получим значение $ \ sin \ theta $ как ноль. Для этого случая мы получим максимальное значение диаграммы напряженности поля, соответствующее главному лепестку . Мы получим максимальные значения картины напряженности поля, соответствующие боковым лепесткам , когда рассмотрим другие значения $ p $.
Направление диаграммы направленности фазированной решетки можно регулировать, изменяя относительные фазы тока, присутствующего в каждой антенне. В этом преимущество электронного сканирования фазированной решетки.