Радарные системы — компенсаторы задержки линии

В этой главе мы узнаем о компенсаторах линии задержки в радиолокационных системах. Как следует из названия, линия задержки вводит определенную величину задержки. Таким образом, линия задержки в основном используется в компенсаторе линии задержки, чтобы ввести задержку времени повторения импульса.

Подавитель линии задержки представляет собой фильтр, который устраняет составляющие постоянного тока эхо-сигналов, полученных от стационарных целей. Это означает, что он допускает компоненты переменного тока эхо-сигналов, полученных от нестационарных целей, то есть движущихся целей.

Типы подавителей линии задержки

Компенсаторы линии задержки могут быть классифицированы на следующие два типа в зависимости от количества линий задержки, которые присутствуют в ней.

• Подавитель одиночной линии задержки
• Линейка с двойной задержкой

В наших последующих разделах мы обсудим больше об этих двух компенсаторах линии задержки.

Подавитель одиночной линии задержки

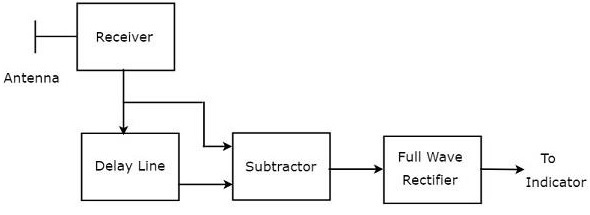
Комбинация линии задержки и вычитателя известна как компенсатор линии задержки. Это также называется однократной задержкой линии задержки. Блок-схема приемника MTI с одним подавителем линии задержки показана на рисунке ниже.

Мы можем записать математическое уравнение принятого эхо-сигнала после эффекта Доплера как —

V1=A sin left[2 pifdt− phi0 right]Equation1 $$V_1 = A \ sin \ left [2 \ pi f_dt- \ phi_0 \ right] \: \: \: \: \: Equation \: 1$$

Куда,

А — амплитуда видеосигнала

$f_d$ — доплеровская частота

$\ phi_o$ — фазовый сдвиг, он равен $4 \ pi f_tR_o / C$

Мы получим вывод средства подавления строки задержки , заменив $t$ на $t-T_P$ в уравнении 1.

V2=A sin left[2 pifd left(t−TP right)− phi0 right]Equation2 $$V_2 = A \ sin \ left [2 \ pi f_d \ left (t-T_P \ right) - \ phi_0 \ right] \: \: \: \: \: Equation \: 2$$

Куда,

$T_P$ — время повторения импульсов

Мы получим результат вычитания путем вычитания уравнения 2 из уравнения 1.

$$V_1-V_2 = A \ sin \ left [2 \ pi f_dt- \ phi_0 \ right] -A \ sin \ left [2 \ pi f_d \ left (t-T_P \ right) - \ phi_0 \ right]$$

$$\ Rightarrow V_1-V_2 = 2A \ sin \ left [\ frac {2 \ pi f_dt- \ phi_0- \ left [2 \ pi f_d \ left (t-T_P \ right) - \ phi_0 \ right]} {2 } \ right] \ cos \ left [\ frac {2 \ pi f_dt- \ phi_o + 2 \ pi f_d \ left (t-T_P \ right) - \ phi_0} {2} \ right]$$

$$V_1-V_2 = 2A \ sin \ left [\ frac {2 \ pi f_dT_P} {2} \ right] \ cos \ left [\ frac {2 \ pi f_d \ left (2t-T_P \ right) -2 \ phi_0} {2} \ right]$$

 RightarrowV1−V2=2A sin left[ pifdTp right] cos left[2 pifd left(t− fracTP2 right)− phi0 right]Уравнение3 $$\ Rightarrow V_1-V_2 = 2A \ sin \ left [\ pi f_dT_p \ right] \ cos \ left [2 \ pi f_d \ left (t- \ frac {T_P} {2} \ right) - \ phi_0 \ right ] \: \: \: \: \: Уравнение \: 3$$

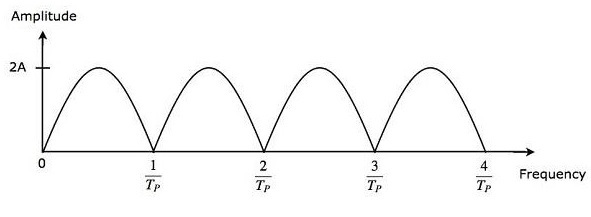
Выход вычитателя применяется как вход для выпрямителя полной волны. Таким образом, вывод выпрямителя Full Wave выглядит так, как показано на следующем рисунке. Это не что иное, как частотная характеристика подавителя линии задержки.

Из уравнения 3 мы можем наблюдать, что частотная характеристика средства подавления одиночной линии задержки становится равной нулю, когда $\ pi f_dT_P$ равно целому числу, кратному $\ pi$. Это означает, что $\ pi f_dT_P$ равно $n \ pi$ Математически это можно записать как

$$\ pi f_dT_P = n \ pi$$

$$\ Rightarrow f_dT_P = n$$

 Rightarrowfd= fracnTPУравнение4 $$\ Rightarrow f_d = \ frac {n} {T_P} \: \: \: \: \: Уравнение \: 4$$

Из уравнения 4 можно сделать вывод, что частотная характеристика компенсатора одиночной линии задержки становится равной нулю, когда доплеровская частота $f_d$ равна целому числу, кратному обратной величине времени повторения импульса $T_P$.

Нам известно следующее соотношение между временем повторения импульса и частотой повторения импульса.

$$f_d = \ гидроразрыва {1} {T_P}$$

 Rightarrow frac1TP=fPEquation5 $$\ Rightarrow \ frac {1} {T_P} = f_P \: \: \: \: \: Equation \: 5$$

Мы получим следующее уравнение, подставив уравнение 5 в уравнение 4.

 Rightarrowfd=nfPEquation6 $$\ Rightarrow f_d = nf_P \: \: \: \: \: Equation \: 6$$

Из уравнения 6 можно сделать вывод, что частотная характеристика компенсатора одиночной линии задержки становится равной нулю, когда доплеровская частота, $f_d$, равна целым кратным частоты повторения импульсов $f_P$.

Слепые скорости

Из того, что мы узнали до сих пор, подавитель одиночной линии задержки устраняет компоненты постоянного тока эхо-сигналов, полученных от стационарных целей, когда $n$ равно нулю. В дополнение к этому он также устраняет компоненты переменного тока эхо-сигналов, принимаемых от нестационарных целей, когда доплеровская частота $f_d$ равна целым (отличным от нуля) кратным частоты повторения импульсов $f_P$.

Таким образом, относительные скорости, для которых частотная характеристика компенсатора одиночной линии задержки становится равной нулю, называются слепыми скоростями . Математически мы можем записать выражение для слепой скорости $v_n$ как —

Vn= гидроразрывап Lambda2TPУравнение7 $$V_n = \ гидроразрыва {п \ Lambda} {2T_P} \: \: \: \: \: Уравнение \: 7$$

 Rightarrowvn= fracn lambdafP2Equation8 $$\ Rightarrow v_n = \ frac {n \ lambda f_P} {2} \: \: \: \: \: Equation \: 8$$

Куда,

$n$ — это целое число, равное 1, 2, 3 и т. д.

$\ lambda$ — рабочая длина волны

Пример задачи

Радар MTI работает на частоте $6 ГГц с частотой повторения импульсов$ 1 КГц. Найдите первую, вторую и третью слепые скорости этого радара.

Решение

Дано,

Рабочая частота MTI Radar, $f = 6 ГГц$

Частота повторения импульсов, $ f_P = 1 кГц.

Ниже приведена формула для рабочей длины волны $\ lambda$ с точки зрения рабочей частоты, f.

$$\ Lambda = \ гидроразрыва {C}, {F}$$

Замените $C = 3 \ times10 ^ 8m / sec$ и $f = 6GHZ$ в вышеприведенном уравнении.

$$\ Lambda = \ гидроразрыва {3 \ times10 ^ 8} {6 \ times10 ^ 9}$$

$$\ Rightarrow \ lambda = 0,05м$$

Таким образом, рабочая длина волны $\ lambda$ равна $0,05 млн., Когда рабочая частота f составляет$ 6 ГГц.

Мы знаем следующую формулу для слепой скорости .

$$v_n = \ frac {n \ lambda f_p} {2}$$

Подставив $n$ = 1,2 & 3 в вышеприведенном уравнении, мы получим следующие уравнения для первой, второй и третьей скоростей блайндов соответственно.

$$v_1 = \ frac {1 \ times \ lambda f_p} {2} = \ frac {\ lambda f_p} {2}$$

$$v_2 = \ frac {2 \ times \ lambda f_p} {2} = 2 \ left (\ frac {\ lambda f_p} {2} \ right) = 2v_1$$

$$v_3 = \ frac {3 \ times \ lambda f_p} {2} = 3 \ left (\ frac {\ lambda f_p} {2} \ right) = 3v_1$$

Подставим значения $\ lambda$ и $f_P$ в уравнение первой слепой скорости.

$$v_1 = \ frac {0.05 \ times 10 ^ 3} {2}$$

$$\ Rightarrow v_1 = 25 м / с$$

Следовательно, первая слепая скорость $v_1$ для данных спецификаций равна $25m / sec$.

Мы получим значения второй и третьей скоростей блайндов как $50 м / с$ и $75 м / с$ соответственно, подставив значение ?1 в уравнения второй и третьей скоростей блайндов.

Линейка с двойной задержкой

Мы знаем, что один компенсатор строки задержки состоит из линии задержки и вычитателя. Если два таких компенсатора линии задержки каскадируются вместе, то эта комбинация называется Двойным компенсатором линии задержки. Блок-схема компенсатора линии двойной задержки показана на следующем рисунке.

Пусть $p \ left (t \ right)$ и $q \ left (t \ right)$ будут входом и выходом первого компенсатора линии задержки. Мы получим следующее математическое соотношение из первого компенсатора линии задержки .

q left(t right)=p left(t right)−p left(t−TP right)Equation9 $$q \ left (t \ right) = p \ left (t \ right) -p \ left (t-T_P \ right) \: \: \: \: \: Equation \: 9$$

Выход первого подавителя строки задержки применяется как вход для второго подавителя строки задержки. Следовательно, $q \ left (t \ right)$ будет входом второго компенсатора линии задержки. Пусть $r \ left (t \ right)$ будет выводом второго компенсатора линии задержки. Мы получим следующее математическое соотношение из второго компенсатора линии задержки .

r left(t right)=q left(t right)−q left(t−TP right)Equation10 $$r \ left (t \ right) = q \ left (t \ right) -q \ left (t-T_P \ right) \: \: \: \: \: Equation \: 10$$

Замените $t$ на $t-T_P$ в уравнении 9.

$$q \ left (t-T_P \ right) = p \ left (t-T_P \ right) -p \ left (t-T_P-T_P \ right)$$

$$q \ left (t-T_P \ right) = p \ left (t-T_P \ right) -p \ left (t-2T_P \ right) \: \: \: \: \: Уравнение \: 11$$

Замените уравнение 9 и уравнение 11 в уравнении 10.

$$r \ left (t \ right) = p \ left (t \ right) -p \ left (t-T_P \ right) - \ left [p \ left (t-T_P \ right) -p \ left (t -2T_P \ right) \ right]$$

$$\ Rightarrow r \ left (t \ right) = p \ left (t \ right) -2p \ left (t-T_P \ right) + p \ left (t-2T_P \ right) \: \: \: \ : \: Уравнение \: 12$$

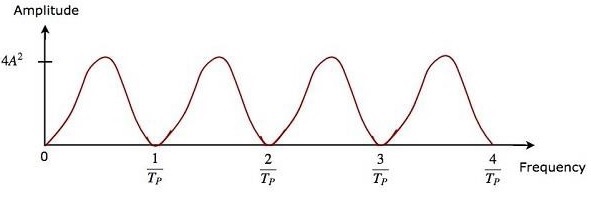
Преимущество двойной линии подавления задержки заключается в том, что она широко отвергает беспорядок. Выход двух компенсаторов линии задержки, которые расположены каскадно, будет равен квадрату выходного сигнала одного компенсатора линии задержки.

Таким образом, величина выходного сигнала компенсатора линии двойной задержки, присутствующего в приемнике MTI Radar, будет равна $4A ^ 2 \ left (\ sin \ left [\ pi f_dT_P \ right] \ right) ^ 2$.

Частотные характеристики как устройства подавления линии с двойной задержкой, так и каскадной комбинации двух устройств подавления линии с задержкой одинаковы. Преимущество подавителя линии задержки во временной области состоит в том, что он может работать для всех частотных диапазонов.