Радарные системы — Обзор

RADAR — это система обнаружения на основе электромагнитного излучения, которая работает, излучая электромагнитные волны, а затем изучая эхо или отраженные обратные волны.

Полной формой RADAR является обнаружение и обнаружение диода RA. Обнаружение относится к тому, присутствует ли цель или нет. Мишень может быть стационарной или подвижной, т.е. нестационарной. Ранжирование относится к расстоянию между радаром и целью.

Радары могут использоваться для различных применений на земле, на море и в космосе. Приложения радаров перечислены ниже.

• Управление воздушным движением
• Безопасность корабля
• Чувство отдаленных мест
• Военные приложения

В любом приложении Радар основной принцип остается тем же. Давайте теперь обсудим принцип радара.

Основной принцип радара

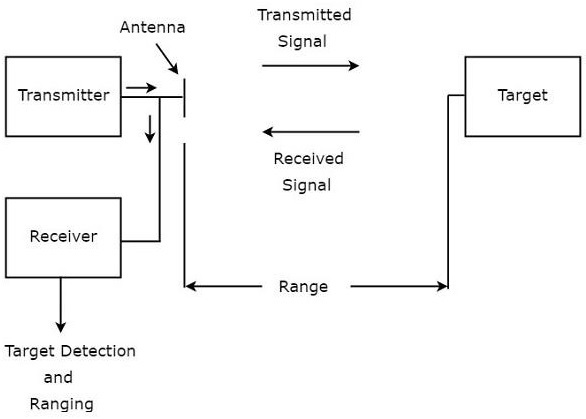
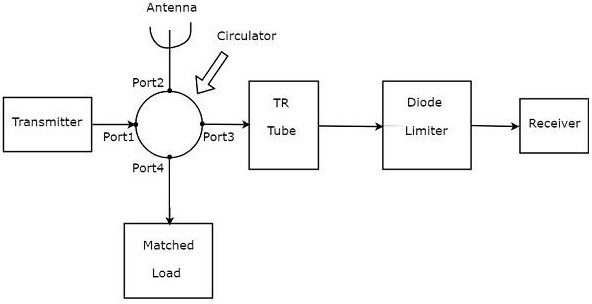
Радар используется для обнаружения объектов и определения их местоположения. Мы можем понять основной принцип радара из следующего рисунка.

Как показано на рисунке, радар в основном состоит из передатчика и приемника. Он использует одну и ту же антенну как для передачи, так и для приема сигналов. Функция передатчика заключается в передаче сигнала радара в направлении присутствующей цели.

Цель отражает этот полученный сигнал в различных направлениях. Сигнал, который отражается обратно к антенне, принимается приемником .

Терминология радиолокационных систем

Ниже приведены основные термины, которые полезны в этом руководстве.

• Спектр
• Частота повторения импульсов
• Максимальный однозначный диапазон
• Минимальный диапазон

Теперь давайте поговорим об этих основных терминах один за другим.

Спектр

Расстояние между радаром и целью называется дальностью цели или просто дальностью R. Мы знаем, что радар передает сигнал к цели и, соответственно, цель посылает эхо-сигнал на радар со скоростью света, C.

Пусть время, необходимое для прохождения сигнала от радара к цели и обратно к радару, будет равно «T». Двустороннее расстояние между радаром и целью будет 2R, поскольку расстояние между радаром и целью составляет R.

Теперь следующая формула для скорости .

$$Speed ​​= \ frac {Расстояние} {Время}$$

$$\ Rightarrow Distance = Скорость \ раз Время$$

$$\ Rightarrow 2R = C \ times T$$

R= гидроразрываКТ2Уравнение1 $$R = \ гидроразрыва {КТ} {2} \: \: \: \: \: Уравнение \: 1$$

Мы можем найти диапазон цели , подставив значения C & T в уравнение 1.

Частота повторения импульсов

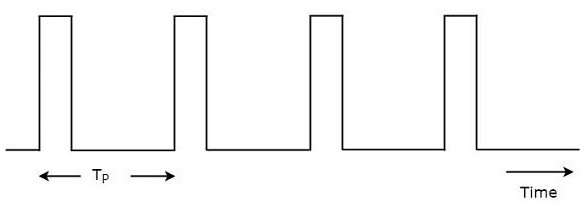
Радарные сигналы должны передаваться при каждом тактовом импульсе. Длительность между двумя тактовыми импульсами должна быть правильно выбрана таким образом, чтобы эхо-сигнал, соответствующий текущему тактовому импульсу, принимался до следующего тактового импульса. Типичная форма волны радара показана на следующем рисунке.

Как показано на рисунке, радар передает периодический сигнал. Он имеет серию узких прямоугольных импульсов. Временной интервал между последовательными тактовыми импульсами называется временем повторения импульсов , $T_P$.

Обратная величина времени повторения импульса называется частотой повторения импульсов , $f_P$. Математически это можно представить как

Fp= гидроразрыва1TPУравнение2 $$F_p = \ гидроразрыва {1} {T_P} \: \: \: \: \: Уравнение \: 2$$

Следовательно, частота повторения импульсов — это не что иное, как частота, на которой радар передает сигнал.

Максимальный однозначный диапазон

Мы знаем, что радарные сигналы должны передаваться при каждом тактовом импульсе. Если мы выберем более короткую длительность между двумя тактовыми импульсами, то эхо-сигнал, соответствующий текущему тактовому импульсу, будет получен после следующего тактового импульса. Из-за этого диапазон цели кажется меньше, чем фактический диапазон.

Таким образом, мы должны выбрать длительность между двумя тактовыми импульсами таким образом, чтобы эхо-сигнал, соответствующий текущему тактовому импульсу, был получен до начала следующего тактового импульса. Затем мы получим истинный диапазон цели, который также называется максимальным однозначным диапазоном цели или просто максимальным однозначным диапазоном .

Замените $R = R_ {un}$ и $T = T_P$ в уравнении 1.

Rип= гидроразрываCTP2Уравнение3 $$R_ {ип} = \ гидроразрыва {CT_P} {2} \: \: \: \: \: Уравнение \: 3$$

Из уравнения 2 мы получим время повторения импульсов, $T_P$ как обратную частоту повторения импульсов, $f_P$. Математически это можно представить как

TP= гидроразрыва1FpУравнение4 $$T_P = \ гидроразрыва {1} {F_p} \: \: \: \: \: Уравнение \: 4$$

Заменить уравнение 4 в уравнении 3.

$$R_ {un} = \ frac {C \ left (\ frac {1} {f_P} \ right)} {2}$$

Rип= гидроразрываC,2fPУравнение5 $$R_ {ип} = \ гидроразрыва {C}, {2f_P} \: \: \: \: \: Уравнение \: 5$$

Мы можем использовать либо Уравнение 3, либо Уравнение 5 для расчета максимального однозначного диапазона цели.

• Мы получим значение максимального однозначного диапазона цели, $R_ {un}$, подставив в уравнение 3 значения $C$ и $T_P$.

• Аналогично, мы получим значение максимального однозначного диапазона цели, $R_ {un}$, подставив в уравнение 5 значения $C$ и $f_P$.

Мы получим значение максимального однозначного диапазона цели, $R_ {un}$, подставив в уравнение 3 значения $C$ и $T_P$.

Аналогично, мы получим значение максимального однозначного диапазона цели, $R_ {un}$, подставив в уравнение 5 значения $C$ и $f_P$.

Минимальный диапазон

Мы получим минимальный диапазон цели, если учесть время, необходимое для получения эхо-сигнала на радаре после передачи сигнала с радара, в качестве ширины импульса. Это также называют самым коротким диапазоном цели.

Замените $R = R_ {min}$ и $T = \ tau$ в уравнении 1.

Rмин= гидроразрываС тау2Уравнение6 $$R_ {} мин = \ гидроразрыва {С \ тау} {2} \: \: \: \: \: Уравнение \: 6$$

Мы получим значение минимального диапазона цели, $R_ {min}$, подставив в уравнение 6 значения $C$ и $\ tau$.

Радарные системы — Уравнение дальности

Радарное уравнение дальности полезно, чтобы узнать дальность цели теоретически . В этой главе мы обсудим стандартную форму уравнения дальности радара, а затем обсудим две модифицированные формы уравнения дальности радара.

Мы получим эти модифицированные формы уравнения дальности радара из стандартной формы уравнения дальности радара. Теперь давайте поговорим о выводе стандартной формы уравнения радиолокационного диапазона.

Вывод уравнения радиолокационной дальности

Стандартная форма радиолокационного уравнения дальности также называется простой формой радиолокационного уравнения дальности. Теперь давайте выведем стандартную форму уравнения радиолокационной дальности.

Мы знаем, что плотность мощности — это не что иное, как соотношение мощности и площади. Таким образом, плотность мощности, $P_ {di}$ на расстоянии R от радара, может быть математически представлена ​​в виде —

Pdi= fracPt4 piR2Equation1 $$P_ {di} = \ frac {P_t} {4 \ pi R ^ 2} \: \: \: \: \: Equation \: 1$$

Куда,

$P_t$ — это мощность, передаваемая радиолокационным передатчиком.

Вышеуказанная плотность мощности действительна для изотропной антенны. В общем, радары используют направленные антенны. Следовательно, плотность мощности, $P_ {dd}$ за счет направленной антенны, составит:

Pdd= fracPtG4 piR2Equation2 $$P_ {dd} = \ frac {P_tG} {4 \ pi R ^ 2} \: \: \: \: \: Equation \: 2$$

Цель излучает мощность в разных направлениях от полученной входной мощности. Количество энергии, которое отражается назад к радару, зависит от его поперечного сечения. Таким образом, плотность мощности $P_ {de}$ эхо-сигнала на радаре может быть математически представлена ​​как —

Pde=Pdd left( frac sigma4 piR2 right)Equation3 $$P_ {de} = P_ {dd} \ left (\ frac {\ sigma} {4 \ pi R ^ 2} \ right) \: \: \: \: \: Equation \: 3$$ Подстановка, Equation 2 в уравнении 3.

Pde= left( fracPtG4 piR2 right) left( frac sigma4 piR2 right)Уравнение4 $$P_ {de} = \ left (\ frac {P_tG} {4 \ pi R ^ 2} \ right) \ left (\ frac {\ sigma} {4 \ pi R ^ 2} \ right) \: \: \: \: \: Уравнение \: 4$$

Количество энергии, $P_r$, полученное Радаром , зависит от эффективной апертуры, $A_e$ принимающей Антенны.

Pr=Р−деAeУравнение5 $$P_r = Р- {} де A_e \: \: \: \: \: Уравнение \: 5$$

Заменить уравнение 4 в уравнении 5.

$$P_r = \ left (\ frac {P_tG} {4 \ pi R ^ 2} \ right) \ left (\ frac {\ sigma} {4 \ pi R ^ 2} \ right) A_e$$

$$\ Rightarrow P_r = \ frac {P_tG \ sigma A_e} {\ left (4 \ pi \ right) ^ 2 R ^ 4}$$

$$\ Rightarrow R ^ 4 = \ frac {P_tG \ sigma A_e} {\ left (4 \ pi \ right) ^ 2 P_r}$$

 RightarrowR= left[ fracPtG sigmaAe left(4 pi right)2Pr right]1/4Уравнение6 $$\ Rightarrow R = \ left [\ frac {P_tG \ sigma A_e} {\ left (4 \ pi \ right) ^ 2 P_r} \ right] ^ {1/4} \: \: \: \: \: Уравнение \: 6$$

Стандартная форма уравнения радиолокационной дальности

Если эхо-сигнал имеет мощность, меньшую мощности минимального обнаруживаемого сигнала, то радар не может обнаружить цель, поскольку он превышает максимальный предел радиолокатора.

Следовательно, можно сказать, что дальность цели называется максимальной, когда принимаемый эхо-сигнал имеет мощность, равную мощности минимального обнаруживаемого сигнала. Мы получим следующее уравнение, подставив $R = R_ {Max}$ и $P_r = S_ {min}$ в уравнение 6.

RMax= left[ fracPtG sigmaAe left(4 pi right)2Smin right]1/4Уравнение7 $$R_ {Max} = \ left [\ frac {P_tG \ sigma A_e} {\ left (4 \ pi \ right) ^ 2 S_ {min}} \ right] ^ {1/4} \: \: \: \: \: Уравнение \: 7$$

Уравнение 7 представляет стандартную форму уравнения радиолокационной дальности. Используя приведенное выше уравнение, мы можем найти максимальную дальность цели.

Модифицированные формы уравнения радиолокационной дальности

Нам известно следующее соотношение между усилением направленной антенны $G$ и эффективной апертурой $A_e$.

G= frac4 piAe lambda2Equation8 $$G = \ frac {4 \ pi A_e} {\ lambda ^ 2} \: \: \: \: \: Equation \: 8$$

Замените уравнение 8 на уравнение 7.

$$R_ {Max} = \ left [\ frac {P_t \ sigma A_e} {\ left (4 \ pi \ right) ^ 2S_ {min}} \ left (\ frac {4 \ pi A_e} {\ lambda ^ 2 } \ right) \ right] ^ {1/4}$$

 RightarrowRMax= left[ fracPtG sigmaAe24 pi lambda2Smin right]1/4Уравнение9 $$\ Rightarrow R_ {Max} = \ left [\ frac {P_tG \ sigma {A_e} ^ 2} {4 \ pi \ lambda ^ 2 S_ {min}} \ right] ^ {1/4} \: \: \: \: \: Уравнение \: 9$$

Уравнение 9 представляет собой модифицированную форму уравнения радиолокационной дальности. Используя приведенное выше уравнение, мы можем найти максимальную дальность цели.

Мы получим следующее соотношение между эффективной апертурой, $A_e$ и усилением направленной антенны, $G$ из уравнения 8.

Ae= гидроразрываG Lambda24 рУравнение10 $$A_e = \ гидроразрыва {G \ Lambda ^ 2} {4 \ р} \: \: \: \: \: Уравнение \: 10$$

Замените уравнение 10 на уравнение 7.

$$R_ {Max} = \ left [\ frac {P_tG \ sigma} {\ left (4 \ pi \ right) ^ 2 S_ {min}} (\ frac {G \ lambda ^ 2} {4 \ pi}) \ right] ^ {1/4}$$

 RightarrowRMax= left[ fracPtG2 lambda2 sigma left(4 pi right)2Smin right]1/4Уравнение11 $$\ Rightarrow R_ {Max} = \ left [\ frac {P_tG ^ 2 \ lambda ^ 2 \ sigma} {\ left (4 \ pi \ right) ^ 2 S_ {min}} \ right] ^ {1/4 } \: \: \: \: \: Уравнение \: 11$$

Уравнение 11 представляет другую модифицированную форму уравнения радиолокационной дальности. Используя приведенное выше уравнение, мы можем найти максимальную дальность цели.

Примечание. На основании приведенных данных мы можем найти максимальный диапазон цели, используя одно из этих трех уравнений, а именно:

• Уравнение 7
• Уравнение 9
• Уравнение 11

Примеры задач

В предыдущем разделе мы получили стандартные и модифицированные формы уравнения радиолокационного диапазона. Теперь давайте решим несколько проблем с помощью этих уравнений.

Проблема 1

Рассчитайте максимальную дальность действия радара для следующих спецификаций —

• Пиковая мощность, передаваемая радаром, $ P_t = 250 кВт
• Усиление передающей антенны, $G = 4000$
• Эффективная апертура приемной антенны, Ae=4m2$A_e = 4 \: m ^ 2$
• Радиолокационное сечение цели,  sigma=25m2$\ sigma = 25 \: m ^ 2$
• Мощность минимально детектируемого сигнала, $S_ {min} = 10 ^ {- 12} Вт$

Решение

Мы можем использовать следующую стандартную форму уравнения дальности радара, чтобы рассчитать максимальную дальность радара для данных спецификаций.

$$R_ {Max} = \ left [\ frac {P_tG \ sigma A_e} {\ left (4 \ pi \ right) ^ 2 S_ {min}} \ right] ^ {1/4}$$

Подставим все приведенные параметры в вышеприведенное уравнение.

$$R_ {Max} = \ left [\ frac {\ left (250 \ times 10 ^ 3 \ right) \ left (4000 \ right) \ left (25 \ right) \ left (4 \ right)} {\ left (4 \ pi \ right) ^ 2 \ left (10 ^ {- 12} \ right)} \ right] ^ {1/4}$$

 RightarrowRMax=158КМ $$\ Rightarrow R_ {Max} = 158 \: КМ$$

Поэтому максимальная дальность действия радара для данных спецификаций составляет 158KM$158 \: KM$.

Проблема 2

Рассчитайте максимальную дальность действия радара для следующих характеристик.

• Рабочая частота, $f = 10 ГГц$
• Пиковая мощность, передаваемая радаром, $ P_t = 400 кВт
• Эффективная апертура приемной антенны, Ae=5m2$A_e = 5 \: m ^ 2$
• Радиолокационное сечение цели,  sigma=30m2$\ sigma = 30 \: m ^ 2$
• Мощность минимально детектируемого сигнала, $S_ {min} = 10 ^ {- 10} Вт$

Решение

Мы знаем следующую формулу для рабочей длины волны , $\ lambda$ в терминах рабочей частоты, f.

$$\ lambda = \ frac {C} {f}$$

Замените $C = 3 \ times 10 ^ 8m / sec$ и $f = 10GHZ$ в вышеприведенном уравнении.

$$\ lambda = \ frac {3 \ times 10 ^ 8} {10 \ times 10 ^ 9}$$

$$\ Rightarrow \ lambda = 0.03m$$

Таким образом, рабочая длина волны $\ lambda$ равна $0,03 млн., Когда рабочая частота$ f $равна$ 10 ГГц.

Мы можем использовать следующую модифицированную форму уравнения дальности радара, чтобы рассчитать максимальную дальность радара для данных спецификаций.

$$R_ {Max} = \ left [\ frac {P_t \ sigma {A_e} ^ 2} {4 \ pi \ lambda ^ 2 S_ {min}} \ right] ^ {1/4}$$

Подставим данные параметры в приведенном выше уравнении.

$$R_ {Max} = \ left [\ frac {\ left (400 \ times 10 ^ 3 \ right) \ left (30 \ right) \ left (5 ^ 2 \ right)} {4 \ pi \ left (0,003 \ right) ^ 2 \ left (10 \ right) ^ {- 10}} \ right] ^ {1/4}$$

$$\ Rightarrow R_ {Max} = 128 КМ$$

Поэтому максимальная дальность действия радара для данных спецификаций составляет 128KM$128 \: KM$.

Радарные системы — факторы производительности

Факторы, которые влияют на производительность радара, известны как факторы производительности радара. В этой главе давайте поговорим об этих факторах. Мы знаем, что приведена следующая стандартная форма уравнения дальности радара, которая полезна для расчета максимальной дальности радара для заданных спецификаций.

$$R_ {Max} = \ left [\ frac {P_tG \ sigma A_e} {\ left (4 \ pi \ right) ^ 2 S_ {min}} \ right] ^ {1/4}$$

Куда,

$P_t$ — пиковая мощность, передаваемая радаром

$G$ — усиление передающей антенны

$\ sigma$ — радиолокационное сечение цели

$A_e$ — эффективная апертура принимающей антенны

$S_ {min}$ — мощность минимального обнаруживаемого сигнала

Из приведенного выше уравнения можно сделать вывод, что для получения максимальной дальности действия радара следует учитывать следующие условия .

• Пиковая мощность, передаваемая радаром $P_t$, должна быть высокой.
• Усиление передающей антенны $G$ должно быть высоким.
• Радиолокационное сечение цели $\ sigma$ должно быть высоким.
• Эффективная апертура приемной антенны $A_e$ должна быть высокой.
• Мощность минимально детектируемого сигнала $S_ {min}$ должна быть низкой.

Трудно предсказать дальность цели из стандартной формы уравнения дальности радара. Это означает, что степень точности, которая обеспечивается уравнением радиолокационного диапазона относительно дальности цели, меньше. Потому что такие параметры, как сечение цели радара, $\ sigma$ и минимально обнаруживаемый сигнал $S_ {min}$, являются статистическими по своему характеру .

Минимальный обнаруживаемый сигнал

Если эхо-сигнал имеет минимальную мощность, обнаружение этого сигнала с помощью радара называется минимальным обнаруживаемым сигналом . Это означает, что радар не может обнаружить эхо-сигнал, если этот сигнал имеет меньшую мощность, чем сигнал минимальной мощности.

В общем, радар получает эхо-сигнал в дополнение к шуму. Если пороговое значение используется для обнаружения присутствия цели из принятого сигнала, то это обнаружение называется пороговым обнаружением .

Мы должны выбрать правильное пороговое значение в зависимости от силы сигнала, который будет обнаружен.

• Высокое пороговое значение следует выбирать, когда интенсивность обнаруживаемого сигнала высока, чтобы исключить присутствующий в нем нежелательный шумовой сигнал.

• Аналогично, низкое пороговое значение следует выбирать, когда сила обнаруживаемого сигнала низкая.

Высокое пороговое значение следует выбирать, когда интенсивность обнаруживаемого сигнала высока, чтобы исключить присутствующий в нем нежелательный шумовой сигнал.

Аналогично, низкое пороговое значение следует выбирать, когда сила обнаруживаемого сигнала низкая.

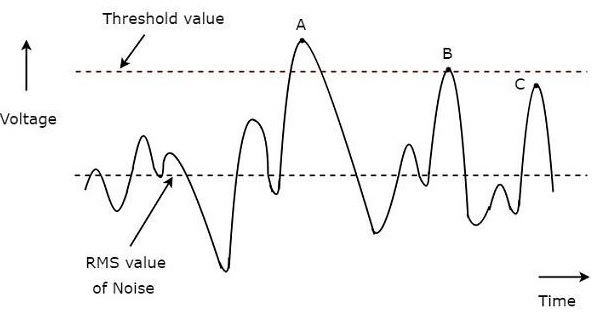
Следующий рисунок иллюстрирует эту концепцию —

Типичная форма сигнала радарного приемника показана на рисунке выше. Ось X и Y представляют время и напряжение соответственно. Среднеквадратичное значение шума и пороговое значение указаны пунктирными линиями на рисунке выше.

Мы рассмотрели три пункта, A, B и C на рисунке выше, для определения допустимых обнаружений и пропущенных обнаружений.

• Значение сигнала в точке A превышает пороговое значение. Следовательно, это действительное обнаружение .

• Значение сигнала в точке B равно пороговому значению. Следовательно, это действительное обнаружение .

• Даже если значение сигнала в точке C ближе к пороговому значению, это пропущенное обнаружение . Потому что значение сигнала в точке C меньше порогового значения.

Значение сигнала в точке A превышает пороговое значение. Следовательно, это действительное обнаружение .

Значение сигнала в точке B равно пороговому значению. Следовательно, это действительное обнаружение .

Даже если значение сигнала в точке C ближе к пороговому значению, это пропущенное обнаружение . Потому что значение сигнала в точке C меньше порогового значения.

Таким образом, точки A и B являются действительными обнаружениями. Принимая во внимание, что точка C является отсутствующим обнаружением.

Шум приемника

Если приемник генерирует шумовую составляющую в сигнале, который принимается в приемнике, то этот вид шума называется шумом приемника. Шум приемника является нежелательным компонентом; мы должны попытаться устранить это с некоторыми мерами предосторожности.

Однако существует один вид шума, известный как тепловой шум. Это происходит из-за теплового движения электронов проводимости. Математически мы можем записать мощность теплового шума , $N_i$, полученную на приемнике, как —

$$N_i = KT_oB_n$$

Куда,

$K$ — постоянная Больцмана, и она равна $1.38 \ times 10 ^ {- 23} Дж / град.$

$T_o$ — абсолютная температура, равная $290 ^ 0K$

$B_n$ — ширина полосы приемника

Фигура заслуги

Показатель заслуг , F — это не что иное, как отношение входного SNR, $(SNR) _i$ и выходного SNR, $(SNR) _o$. Математически это можно представить как —

$$F = \ {гидроразрыва (SNR),-i} {(SNR), _o}$$

$$\ Rightarrow F = \ frac {S_i / N_i} {S_o / N_o}$$

$$\ Rightarrow F = \ frac {N_oS_i} {N_iS_o}$$

$$\ Rightarrow S_i = \ frac {FN_iS_o} {N_o}$$

Замените $N_i = KT_oB_n$ в приведенном выше уравнении.

$$\ Rightarrow S_i = FKT_oB_n \ left (\ frac {S_o} {N_o} \ right)$$

Мощность входного сигнала будет иметь минимальное значение, когда выходное SNR имеет минимальное значение.

$$\ Rightarrow S_ {min} = FKT_oB_n \ left (\ frac {S_o} {N_o} \ right) _ {min}$$

Замените вышеуказанное $S_ {min}$ в следующей стандартной форме уравнения радиолокационной дальности.

$$R_ {Max} = \ left [\ frac {P_tG \ sigma A_e} {\ left (4 \ pi \ right) ^ 2 S_ {min}} \ right] ^ {1/4}$$

$$\ Rightarrow R_ {Max} = \ left [\ frac {P_tG \ sigma A_e} {\ left (4 \ pi \ right) ^ 2 FKT_oB_n \ left (\ frac {S_o} {N_o} \ right) _ {мин }} \ right] ^ {1/4}$$

Из приведенного выше уравнения можно сделать вывод, что для получения максимальной дальности действия радара следует учитывать следующие условия .

• Пиковая мощность, передаваемая радаром, $P_t$ должна быть высокой.
• Усиление передающей антенны $G$ должно быть высоким.
• Радиолокационное сечение цели $\ sigma$ должно быть высоким.
• Эффективная апертура приемной антенны $A_e$ должна быть высокой.
• Показатель заслуг F должен быть низким.
• Пропускная способность приемника $B_n$ должна быть низкой.

Радарные Системы — Типы Радаров

В этой главе мы кратко обсудим различные типы радаров. В этой главе приводится краткая информация о типах радаров. Радары могут быть классифицированы на следующие два типа в зависимости от типа сигнала, с которым можно работать.

• Импульсный радар
• Радар с непрерывной волной

Теперь давайте поговорим об этих двух типах радаров один за другим.

Импульсный радар

Радар, который работает с импульсным сигналом, называется импульсным радаром . Импульсные радары могут быть классифицированы на следующие два типа в зависимости от типа обнаруживаемой цели.

• Основной импульсный радар
• Индикатор движущейся цели

Давайте теперь кратко обсудим два радара.

Основной импульсный радар

Радар, который работает с импульсным сигналом для обнаружения стационарных целей, называется базовым импульсным радаром или просто импульсным радаром. Он использует одну антенну для передачи и приема сигналов с помощью дуплексера.

Антенна будет передавать импульсный сигнал при каждом тактовом импульсе. Длительность между двумя тактовыми импульсами должна выбираться таким образом, чтобы эхо-сигнал, соответствующий текущему тактовому импульсу, принимался до следующего тактового импульса.

Индикатор движущейся цели

Радар, который работает с импульсным сигналом для обнаружения нестационарных целей, называется радаром индикации движущейся цели или просто MTI Radar . Он использует одну антенну для передачи и приема сигналов с помощью дуплексера.

MTI Radar использует принцип эффекта Доплера для различения нестационарных целей от стационарных объектов.

Радар с непрерывной волной

Радар, который работает с непрерывным сигналом или волной, называется радаром с непрерывной волной . Они используют эффект Доплера для обнаружения нестационарных целей. Радары с непрерывной волной можно классифицировать на следующие два типа.

• Немодулированный радиолокатор с непрерывной волной
• Радар с непрерывной волной и частотной модуляцией

Теперь давайте кратко обсудим два радара.

Немодулированный радиолокатор с непрерывной волной

Радар, который работает с непрерывным сигналом (волной) для обнаружения нестационарных целей, называется немодулированным радаром с непрерывной волной или просто CW Radar . Он также называется CW Doppler Radar.

Этот радар требует двух антенн. Из этих двух антенн одна антенна используется для передачи сигнала, а другая антенна используется для приема сигнала. Он измеряет только скорость цели, но не расстояние цели от радара.

Радар с непрерывной волной и частотной модуляцией

Если CW Doppler Radar использует частотную модуляцию, то этот радар называется радаром с частотно-модулированной непрерывной волной (FMCW) или доплеровским радаром FMCW. Он также называется радиолокатором с непрерывной частотной модуляцией или радиолокатором CWFM.

Этот радар требует двух антенн. Среди которых одна антенна используется для передачи сигнала, а другая антенна используется для приема сигнала. Он измеряет не только скорость цели, но и расстояние до цели от радара.

В наших последующих главах мы подробно обсудим работу всех этих радаров.

Радарные Системы — Импульсный Радар

Радар, который работает с импульсным сигналом для обнаружения стационарных целей, называется базовым импульсным радаром или просто импульсным радаром . В этой главе давайте обсудим работу импульсного радара.

Блок-схема импульсного радара

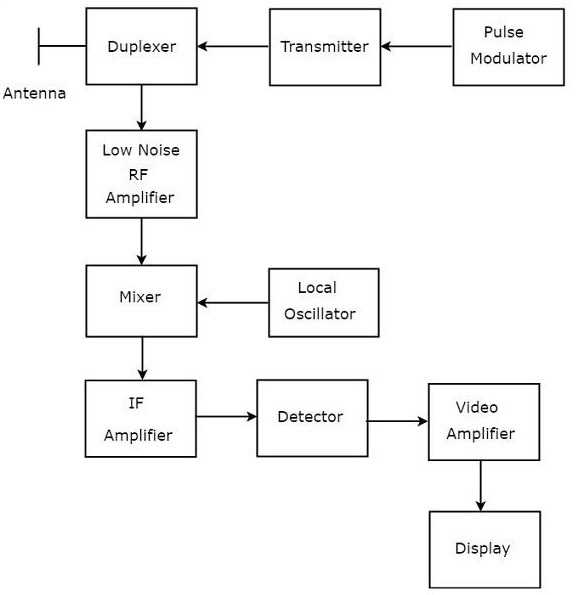
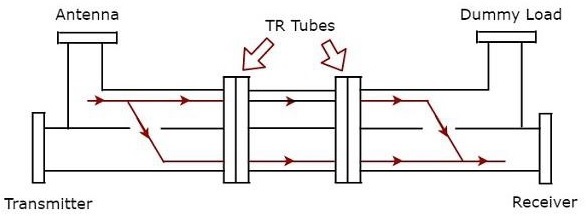
Импульсный радар использует одну антенну для передачи и приема сигналов с помощью дуплексера. Ниже приведена блок-схема импульсного радара —

Давайте теперь посмотрим на функцию каждого блока импульсного радара —

• Импульсный модулятор — он генерирует импульсный сигнал и подается на передатчик.

• Передатчик — передает импульсно-модулированный сигнал, представляющий собой последовательность повторяющихся импульсов.

• Дуплексер — это микроволновый переключатель, который попеременно соединяет Антенну и с секцией передатчика, и с секцией приемника. Антенна передает импульсно-модулированный сигнал, когда дуплексер подключает антенну к передатчику. Аналогичным образом, сигнал, который принимается антенной, передается на РЧ-усилитель с низким уровнем шума, когда дуплексер подключает Антенну к РЧ-усилителю с низким уровнем шума.

• РЧ-усилитель с низким уровнем шума — усиливает слабый РЧ-сигнал, принимаемый антенной. Выход этого усилителя подключен к микшеру.

• Локальный генератор — генерирует сигнал, имеющий стабильную частоту. Выход локального генератора подключен к микшеру.

• Микшер — мы знаем, что микшер может производить как сумму, так и разницу частот, которые к нему применяются. Среди которых разность частот будет иметь тип промежуточной частоты (IF).

• Усилитель ПЧ — усилитель ПЧ усиливает сигнал промежуточной частоты (ПЧ). Усилитель ПЧ, показанный на рисунке, допускает только промежуточную частоту, которая получается из микшера и усиливает ее. Это улучшает отношение сигнал / шум на выходе.

• Детектор — демодулирует сигнал, который получается на выходе усилителя ПЧ.

• Усилитель видео — как следует из названия, он усиливает видеосигнал, который получается на выходе детектора.

• Дисплей — В общем, он отображает усиленный видеосигнал на экране ЭЛТ.

Импульсный модулятор — он генерирует импульсный сигнал и подается на передатчик.

Передатчик — передает импульсно-модулированный сигнал, представляющий собой последовательность повторяющихся импульсов.

Дуплексер — это микроволновый переключатель, который попеременно соединяет Антенну и с секцией передатчика, и с секцией приемника. Антенна передает импульсно-модулированный сигнал, когда дуплексер подключает антенну к передатчику. Аналогичным образом, сигнал, который принимается антенной, передается на РЧ-усилитель с низким уровнем шума, когда дуплексер подключает Антенну к РЧ-усилителю с низким уровнем шума.

РЧ-усилитель с низким уровнем шума — усиливает слабый РЧ-сигнал, принимаемый антенной. Выход этого усилителя подключен к микшеру.

Локальный генератор — генерирует сигнал, имеющий стабильную частоту. Выход локального генератора подключен к микшеру.

Микшер — мы знаем, что микшер может производить как сумму, так и разницу частот, которые к нему применяются. Среди которых разность частот будет иметь тип промежуточной частоты (IF).

Усилитель ПЧ — усилитель ПЧ усиливает сигнал промежуточной частоты (ПЧ). Усилитель ПЧ, показанный на рисунке, допускает только промежуточную частоту, которая получается из микшера и усиливает ее. Это улучшает отношение сигнал / шум на выходе.

Детектор — демодулирует сигнал, который получается на выходе усилителя ПЧ.

Усилитель видео — как следует из названия, он усиливает видеосигнал, который получается на выходе детектора.

Дисплей — В общем, он отображает усиленный видеосигнал на экране ЭЛТ.

В этой главе мы обсудили, как работает импульсный радар и как он полезен для обнаружения стационарных целей. В наших последующих главах мы обсудим радары, которые полезны для обнаружения нестационарных целей.

Радарные системы — эффект Доплера

В этой главе мы узнаем об эффекте Доплера в радиолокационных системах.

Если цель не является стационарной, то произойдет изменение частоты сигнала, который передается с радара и который принимается радаром. Этот эффект известен как эффект Доплера .

В соответствии с эффектом Доплера мы получим два возможных случая:

• Частота принимаемого сигнала будет увеличиваться , когда цель движется в направлении радара.

• Частота принимаемого сигнала будет уменьшаться , когда цель удаляется от радара.

Частота принимаемого сигнала будет увеличиваться , когда цель движется в направлении радара.

Частота принимаемого сигнала будет уменьшаться , когда цель удаляется от радара.

Теперь давайте выведем формулу для доплеровской частоты.

Вывод доплеровской частоты

Расстояние между радаром и целью является ничем иным, как дальностью цели или просто дальностью R. Следовательно, общее расстояние между радаром и целью на двусторонней линии связи будет равно 2R, поскольку радар передает сигнал к цели и соответственно цель посылает эхо-сигнал на радар.

Если $\ lambda$ — одна длина волны, то число длин волн N, которые присутствуют в двухстороннем пути связи между радаром и целью, будет равно $2R / \ lambda$.

Мы знаем, что одной длине волны $\ lambda$ соответствует угловая экскурсия в $2 \ pi$ радиан. Таким образом, общий угол отклонения, создаваемого электромагнитной волной во время двусторонней связи между радаром и целью, будет равен $4 \ pi R / \ lambda$ радиан.

Ниже приводится математическая формула для угловой частоты , $\ omega$ —

$$\ omega = 2 \ pi f \: \: \: \: \: Equation \: 1$$

Следующее уравнение показывает математическое соотношение между угловой частотой $\ omega$ и фазовым углом $\ phi$ —

$$\ omega = \ frac {d \ phi} {dt} \: \: \: \: \: Equation \: 2$$

Выравнивайте правые члены уравнения 1 и 2, поскольку левые члены этих двух уравнений одинаковы.

$$2 \ pi f = \ frac {d \ phi} {dt}$$

$$\ Rightarrow f = \ frac {1} {2 \ pi} \ frac {d \ phi} {dt} \: \: \: \: \: Equation \: 3$$

Замените $f = f_d$ и $\ phi = 4 \ pi R / \ lambda$ в уравнении 3.

$$f_d = \ frac {1} {2 \ pi} \ frac {d} {dt} \ left (\ frac {4 \ pi R} {\ lambda} \ right)$$

$$\ Rightarrow f_d = \ frac {1} {2 \ pi} \ frac {4 \ pi} {\ lambda} \ frac {dR} {dt}$$

$$\ Rightarrow f_d = \ frac {2V_r} {\ lambda} \: \: \: \: \: Equation \: 4$$

Куда,

$f_d$ — доплеровская частота

$V_r$ — относительная скорость

Мы можем найти значение доплеровской частоты $f_d$, подставив в уравнение 4 значения $V_r$ и $\ lambda$.

Замените $\ lambda = C / f$ в уравнении 4.

$$f_d = \ frac {2V_r} {C / f}$$

$$\ Rightarrow f_d = \ frac {2V_rf} {C} \: \: \: \: \: Equation \: 5$$

Куда,

$f$ — частота передаваемого сигнала

$C$ — это скорость света, и она равна $3 \ times 10 ^ 8m / sec$

Мы можем найти значение доплеровской частоты $f_d$, подставив в уравнение 5 значения $V_r, f$ и $C$.

Примечание. Как в уравнении 4, так и в уравнении 5 показаны формулы доплеровской частоты $f_d$. Мы можем использовать уравнение 4 или уравнение 5 для нахождения доплеровской частоты , $f_d$, основываясь на данных.

Пример задачи

Если радар работает на частоте 5 ГГц, найдите доплеровскую частоту самолета, движущегося со скоростью 100 км / ч.

Решение

Дано,

Частота передаваемого сигнала, $f = 5 ГГц$

Скорость самолета (цель), $ V_r = 100 км / ч

$$\ Rightarrow V_r = \ frac {100 \ times 10 ^ 3} {3600} м / с$$

$$\ Rightarrow V_r = 27,78 м / с$$

Мы конвертировали заданную скорость самолета (цель), которая присутствует в км / ч, в эквивалентную м / с.

Мы знаем, что скорость света, $C = 3 \ умножить на 10 ^ 8 м / с$

Теперь следующая формула для доплеровской частоты —

$$f_d = \ гидроразрыва {2Vrf} {C}$$

Подставим значения 𠑉 ð’ Ÿ, $V_r, f$ и $C$ в вышеприведенное уравнение.

$$\ Rightarrow f_d = \ frac {2 \ left (27.78 \ right) \ left (5 \ times 10 ^ 9 \ right)} {3 \ times 10 ^ 8}$$

$$\ Rightarrow f_d = 926HZ$$

Поэтому значение доплеровской частоты $f_d$ составляет 926 Гц $ для данных спецификаций.

Радарные системы — CW Radar

Базовый радар использует одну и ту же антенну для передачи и приема сигналов. Мы можем использовать этот тип радара, когда цель неподвижна, то есть не движется, и / или когда этот радар может работать с импульсным сигналом.

Радар, который работает с непрерывным сигналом (волной) для обнаружения нестационарных целей, называется непрерывным волновым радаром или просто CW Radar . Этот радар требует двух антенн. Среди которых одна антенна используется для передачи сигнала, а другая антенна используется для приема сигнала.

Блок-схема CW Radar

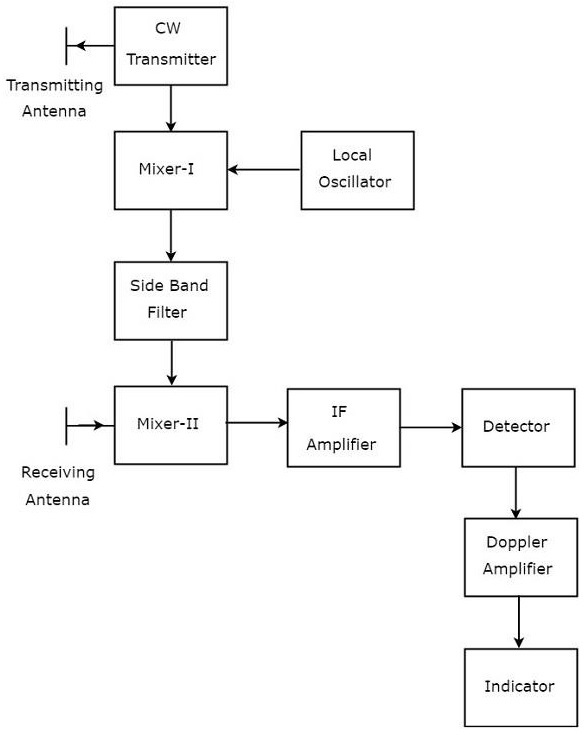
Мы знаем, что CW Doppler Radar содержит две антенны — передающую антенну и принимающую антенну. На следующем рисунке показана блок-схема CW Radar —

Блок-схема доплеровского радара CW содержит набор блоков, и функция каждого блока указана ниже.

• CW Transmitter — генерирует аналоговый сигнал с частотой $f_o$. Выход передатчика CW подключен как к передающей антенне, так и к Mixer-I.

• Локальный генератор — генерирует сигнал с частотой $f_l$. Выход локального генератора подключен к микшеру-I.

• Mixer-I — Mixer может производить как сумму, так и разницу частот, которые к нему применяются. Сигналы, имеющие частоты $f_o$ и $f_l$, подаются на Mixer-I. Итак, Mixer-I выдаст выходные данные с частотами $f_o + f_l$ или $f_o − f_l$.

• Фильтр боковой полосы — Как следует из названия, фильтр боковой полосы допускает определенные частоты боковой полосы — либо частоты верхней боковой полосы, либо частоты нижней боковой полосы. Фильтр боковой полосы, показанный на приведенном выше рисунке, генерирует только частоту верхней боковой полосы, то есть $f_o + f_l$.

• Mixer-II — Mixer может производить как сумму, так и разницу частот, которые к нему применяются. Сигналы, имеющие частоты $f_o + f_l$ и $f_o \ pm f_d$, подаются на Mixer-II. Итак, Mixer-II будет выдавать выходные данные с частотами 2 $f_o + f_l \ pm f_d$ или $f_l \ pm f_d$.

• Усилитель ПЧ — усилитель ПЧ усиливает сигнал промежуточной частоты (ПЧ). Усилитель ПЧ, показанный на рисунке, допускает только промежуточную частоту $f_l \ pm f_d$ и усиливает ее.

• Детектор — обнаруживает сигнал с доплеровской частотой $f_d$.

• Допплеровский усилитель. Как следует из названия, доплеровский усилитель усиливает сигнал, имеющий доплеровскую частоту, $f_d$.

• Индикатор — указывает относительную скорость, относящуюся к информации, и является ли цель входящей или исходящей.

CW Transmitter — генерирует аналоговый сигнал с частотой $f_o$. Выход передатчика CW подключен как к передающей антенне, так и к Mixer-I.

Локальный генератор — генерирует сигнал с частотой $f_l$. Выход локального генератора подключен к микшеру-I.

Mixer-I — Mixer может производить как сумму, так и разницу частот, которые к нему применяются. Сигналы, имеющие частоты $f_o$ и $f_l$, подаются на Mixer-I. Итак, Mixer-I выдаст выходные данные с частотами $f_o + f_l$ или $f_o − f_l$.

Фильтр боковой полосы — Как следует из названия, фильтр боковой полосы допускает определенные частоты боковой полосы — либо частоты верхней боковой полосы, либо частоты нижней боковой полосы. Фильтр боковой полосы, показанный на приведенном выше рисунке, генерирует только частоту верхней боковой полосы, то есть $f_o + f_l$.

Mixer-II — Mixer может производить как сумму, так и разницу частот, которые к нему применяются. Сигналы, имеющие частоты $f_o + f_l$ и $f_o \ pm f_d$, подаются на Mixer-II. Итак, Mixer-II будет выдавать выходные данные с частотами 2 $f_o + f_l \ pm f_d$ или $f_l \ pm f_d$.

Усилитель ПЧ — усилитель ПЧ усиливает сигнал промежуточной частоты (ПЧ). Усилитель ПЧ, показанный на рисунке, допускает только промежуточную частоту $f_l \ pm f_d$ и усиливает ее.

Детектор — обнаруживает сигнал с доплеровской частотой $f_d$.

Допплеровский усилитель. Как следует из названия, доплеровский усилитель усиливает сигнал, имеющий доплеровскую частоту, $f_d$.

Индикатор — указывает относительную скорость, относящуюся к информации, и является ли цель входящей или исходящей.

Радары CW Doppler дают точное измерение относительных скоростей . Следовательно, они используются в основном там, где информация о скорости важнее, чем фактический диапазон.

Радарные Системы — FMCW Радар

Если CW Doppler Radar использует частотную модуляцию, то этот радар называется FMCW Doppler Radar или просто FMCW Radar . Он также называется радиолокатором с непрерывной частотной модуляцией или радиолокатором CWFM. Он измеряет не только скорость цели, но и расстояние до цели от радара.

Блок-схема радара FMCW

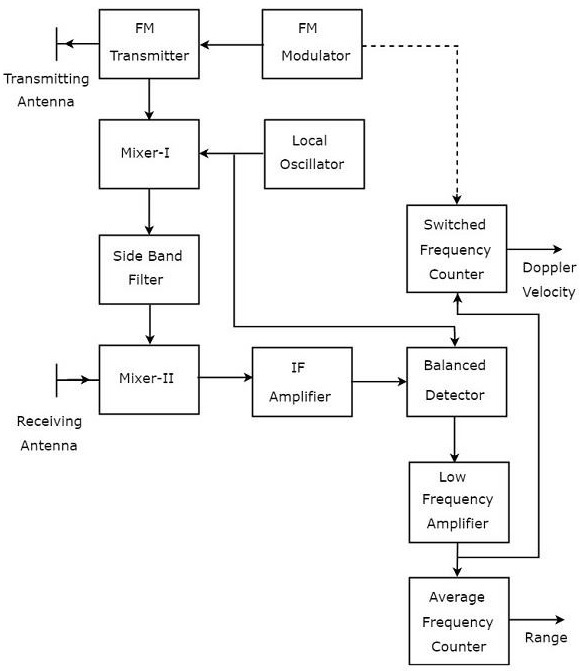
Радиолокатор FMCW в основном используется в качестве радиолокационного высотомера для измерения точной высоты при посадке самолета. На следующем рисунке показана блок-схема радара FMCW —

Радар FMCW содержит две антенны — передающую антенну и принимающую антенну, как показано на рисунке. Передающая антенна передает сигнал, а принимающая антенна принимает эхо-сигнал.

Блок-схема радара FMCW выглядит аналогично блок-схеме радара CW. Он содержит несколько модифицированных блоков и некоторые другие блоки в дополнение к блокам, которые присутствуют в блок-схеме CW Radar. Функция каждого блока FMCW Radar указана ниже.

• FM-модулятор — он генерирует частотно-модулированный (FM) сигнал с переменной частотой $f_o \ left (t \ right)$ и применяется к FM-передатчику.

• FM-передатчик — передает FM-сигнал с помощью передающей антенны. Выход FM-передатчика также подключен к Mixer-I.

• Локальный генератор — В общем, локальный генератор используется для получения радиочастотного сигнала. Но здесь он используется для получения сигнала, имеющего промежуточную частоту, $f_ {IF}$. Выход локального генератора подключен к микшеру-I и симметричному детектору.

• Mixer-I — Mixer может производить как сумму, так и разницу частот, которые к нему применяются. Сигналы с частотами $f_o \ left (t \ right)$ и $f_ {IF}$ подаются на Mixer-I. Таким образом, Mixer-I будет генерировать выходные данные с частотой $f_o \ left (t \ right) + f_ {IF}$ или $f_o \ left (t \ right) -f_ {IF}$.

• Фильтр боковой полосы — он допускает только частоты одной боковой полосы, то есть либо частоты верхней боковой полосы, либо частоты нижней боковой полосы. Фильтр боковой полосы, показанный на рисунке, производит только частоту нижней полосы. то есть $f_o \ left (t \ right) -f_ {IF}$.

• Mixer-II — Mixer может производить как сумму, так и разницу частот, которые к нему применяются. Сигналы с частотами $f_o \ left (t \ right) -f_ {IF}$ и $f_o \ left (tT \ right)$ подаются на Mixer-II. Таким образом, Mixer-II будет производить вывод с частотой: либо $f_o \ left (tT \ right) + f_o \ left (t \ right) -f_ {IF}$, либо $f_o \ left (tT \ right) -f_o \ влево (t \ right) + f_ {IF}$.

• Усилитель ПЧ — усилитель ПЧ усиливает сигнал промежуточной частоты (ПЧ). Усилитель ПЧ, показанный на рисунке, усиливает сигнал с частотой $f_o \ left (tT \ right) -f_o \ left (t \ right) + f_ {IF}$. Этот усиленный сигнал подается в качестве входа на сбалансированный детектор.

• Сбалансированный детектор — используется для получения выходного сигнала с частотой $f_o \ left (tT \ right) -f_o \ left (t \ right)$ из двух примененных входных сигналов, которые имеют частоты $f_o \ left ( tT \ right) -f_o \ left (t \ right) + f_ {IF}$ и $f_ {IF}$. Выход сбалансированного детектора используется в качестве входа для усилителя низкой частоты.

• Усилитель низких частот — усиливает выход сбалансированного детектора до требуемого уровня. Выход низкочастотного усилителя подается на счетчик с переключаемой частотой и на счетчик средней частоты.

• Счетчик частоты переключения — полезен для получения значения доплеровской скорости.

• Счетчик средней частоты — это полезно для получения значения диапазона.

FM-модулятор — он генерирует частотно-модулированный (FM) сигнал с переменной частотой $f_o \ left (t \ right)$ и применяется к FM-передатчику.

FM-передатчик — передает FM-сигнал с помощью передающей антенны. Выход FM-передатчика также подключен к Mixer-I.

Локальный генератор — В общем, локальный генератор используется для получения радиочастотного сигнала. Но здесь он используется для получения сигнала, имеющего промежуточную частоту, $f_ {IF}$. Выход локального генератора подключен к микшеру-I и симметричному детектору.

Mixer-I — Mixer может производить как сумму, так и разницу частот, которые к нему применяются. Сигналы с частотами $f_o \ left (t \ right)$ и $f_ {IF}$ подаются на Mixer-I. Таким образом, Mixer-I будет генерировать выходные данные с частотой $f_o \ left (t \ right) + f_ {IF}$ или $f_o \ left (t \ right) -f_ {IF}$.

Фильтр боковой полосы — он допускает только частоты одной боковой полосы, то есть либо частоты верхней боковой полосы, либо частоты нижней боковой полосы. Фильтр боковой полосы, показанный на рисунке, производит только частоту нижней полосы. то есть $f_o \ left (t \ right) -f_ {IF}$.

Mixer-II — Mixer может производить как сумму, так и разницу частот, которые к нему применяются. Сигналы с частотами $f_o \ left (t \ right) -f_ {IF}$ и $f_o \ left (tT \ right)$ подаются на Mixer-II. Таким образом, Mixer-II будет производить вывод с частотой: либо $f_o \ left (tT \ right) + f_o \ left (t \ right) -f_ {IF}$, либо $f_o \ left (tT \ right) -f_o \ влево (t \ right) + f_ {IF}$.

Усилитель ПЧ — усилитель ПЧ усиливает сигнал промежуточной частоты (ПЧ). Усилитель ПЧ, показанный на рисунке, усиливает сигнал с частотой $f_o \ left (tT \ right) -f_o \ left (t \ right) + f_ {IF}$. Этот усиленный сигнал подается в качестве входа на сбалансированный детектор.

Сбалансированный детектор — используется для получения выходного сигнала с частотой $f_o \ left (tT \ right) -f_o \ left (t \ right)$ из двух примененных входных сигналов, которые имеют частоты $f_o \ left ( tT \ right) -f_o \ left (t \ right) + f_ {IF}$ и $f_ {IF}$. Выход сбалансированного детектора используется в качестве входа для усилителя низкой частоты.

Усилитель низких частот — усиливает выход сбалансированного детектора до требуемого уровня. Выход низкочастотного усилителя подается на счетчик с переключаемой частотой и на счетчик средней частоты.

Счетчик частоты переключения — полезен для получения значения доплеровской скорости.

Счетчик средней частоты — это полезно для получения значения диапазона.

Радарные Системы — MTI Радар

Если радар используется для обнаружения подвижной цели, тогда радар должен получать только эхо-сигнал от этой подвижной цели. Этот эхо-сигнал является желаемым. Однако в практических применениях Радар принимает эхо-сигналы от стационарных объектов в дополнение к эхо-сигналу от этой подвижной цели.

Эхо-сигналы от стационарных объектов (мест), таких как суша и море, называются помехами, потому что это нежелательные сигналы. Поэтому мы должны выбирать радар таким образом, чтобы он учитывал только эхо-сигнал из-за подвижной цели, но не из-за помех.

Для этого Радар использует принцип эффекта Доплера для различения нестационарных целей от стационарных объектов. Этот тип радара называется индикатором движущейся цели или просто MTI Radar .

Согласно эффекту Доплера , частота принимаемого сигнала будет увеличиваться, если цель движется в направлении радара. Аналогичным образом частота принимаемого сигнала будет уменьшаться, если цель удаляется от радара.

Типы MTI Радары

Мы можем классифицировать радары MTI по ​​следующим двум типам в зависимости от типа используемого передатчика.

• Радар MTI с усилителем мощности и передатчиком
• Радар MTI с передатчиком генератора мощности

Теперь давайте поговорим об этих двух радарах MTI один за другим.

Радар MTI с усилителем мощности и передатчиком

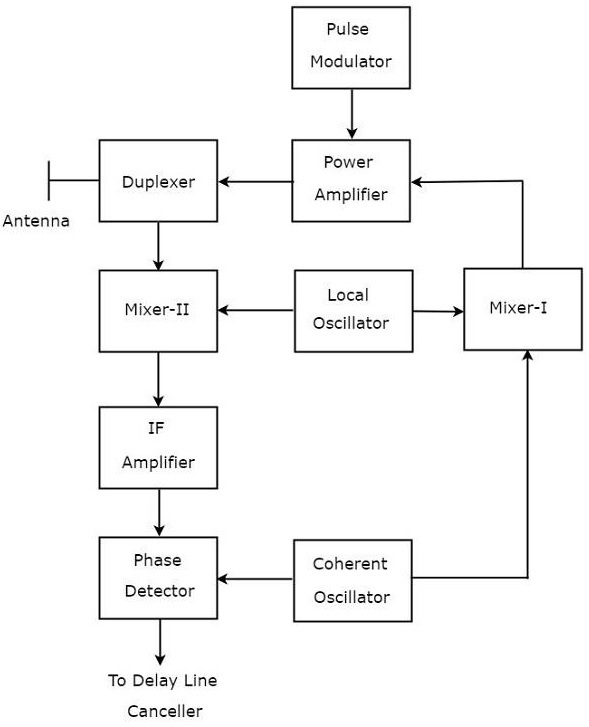
MTI Radar использует единую антенну для передачи и приема сигналов с помощью дуплексера. Блок-схема MTI Radar с усилителем мощности передатчика показана на следующем рисунке.

Функция каждого блока MTI Radar с передатчиком усилителя мощности указана ниже.

• Импульсный модулятор — генерирует импульсный сигнал и применяется к усилителю мощности.

• Усилитель мощности — усиливает уровни мощности сигнала с импульсной модуляцией.

• Локальный генератор — генерирует сигнал со стабильной частотой $f_l$. Следовательно, он также называется стабильным локальным генератором. Выход Локального генератора применяется как к Миксеру-I, так и к Миксеру-II.

• Когерентный генератор — формирует сигнал с промежуточной частотой $f_c$. Этот сигнал используется в качестве опорного сигнала. Выходной сигнал когерентного генератора подается на микшер-I и фазовый детектор.

• Mixer-I — Mixer может производить либо сумму, либо разницу частот, которые к нему применяются. Сигналы с частотами $f_l$ и $f_c$ подаются на Mixer-I. Здесь Mixer-I используется для получения выходного сигнала, который имеет частоту $f_l + f_c$.

• Дуплексер — это микроволновый коммутатор, который подключает антенну либо к секции передатчика, либо к секции приемника в зависимости от требований. Антенна передает сигнал с частотой $f_l + f_c$, когда дуплексер подключает антенну к усилителю мощности. Аналогично, антенна принимает сигнал с частотой $f_l + f_c \ pm f_d$, когда дуплексер соединяет антенну с микшером-II.

• Mixer-II — Mixer может производить либо сумму, либо разницу частот, которые к нему применяются. Сигналы, имеющие частоты $f_l + f_c \ pm f_d$ и $f_l$, подаются на Mixer-II. Здесь Mixer-II используется для создания выходного сигнала, который имеет частоту $f_c \ pm f_d$.

• Усилитель ПЧ — усилитель ПЧ усиливает сигнал промежуточной частоты (ПЧ). Усилитель ПЧ, показанный на рисунке, усиливает сигнал с частотой $f_c + f_d$. Этот усиленный сигнал подается на вход фазового детектора.

Импульсный модулятор — генерирует импульсный сигнал и применяется к усилителю мощности.

Усилитель мощности — усиливает уровни мощности сигнала с импульсной модуляцией.

Локальный генератор — генерирует сигнал со стабильной частотой $f_l$. Следовательно, он также называется стабильным локальным генератором. Выход Локального генератора применяется как к Миксеру-I, так и к Миксеру-II.

Когерентный генератор — формирует сигнал с промежуточной частотой $f_c$. Этот сигнал используется в качестве опорного сигнала. Выходной сигнал когерентного генератора подается на микшер-I и фазовый детектор.

Mixer-I — Mixer может производить либо сумму, либо разницу частот, которые к нему применяются. Сигналы с частотами $f_l$ и $f_c$ подаются на Mixer-I. Здесь Mixer-I используется для получения выходного сигнала, который имеет частоту $f_l + f_c$.

Дуплексер — это микроволновый коммутатор, который подключает антенну либо к секции передатчика, либо к секции приемника в зависимости от требований. Антенна передает сигнал с частотой $f_l + f_c$, когда дуплексер подключает антенну к усилителю мощности. Аналогично, антенна принимает сигнал с частотой $f_l + f_c \ pm f_d$, когда дуплексер соединяет антенну с микшером-II.

Mixer-II — Mixer может производить либо сумму, либо разницу частот, которые к нему применяются. Сигналы, имеющие частоты $f_l + f_c \ pm f_d$ и $f_l$, подаются на Mixer-II. Здесь Mixer-II используется для создания выходного сигнала, который имеет частоту $f_c \ pm f_d$.

Усилитель ПЧ — усилитель ПЧ усиливает сигнал промежуточной частоты (ПЧ). Усилитель ПЧ, показанный на рисунке, усиливает сигнал с частотой $f_c + f_d$. Этот усиленный сигнал подается на вход фазового детектора.

Фазовый детектор — используется для получения выходного сигнала с частотой $f_d$ из двух поданных входных сигналов с частотами $f_c + f_d$ и $f_c$. Выход фазового детектора может быть подключен к подавителю линии задержки.

Радар MTI с передатчиком генератора мощности

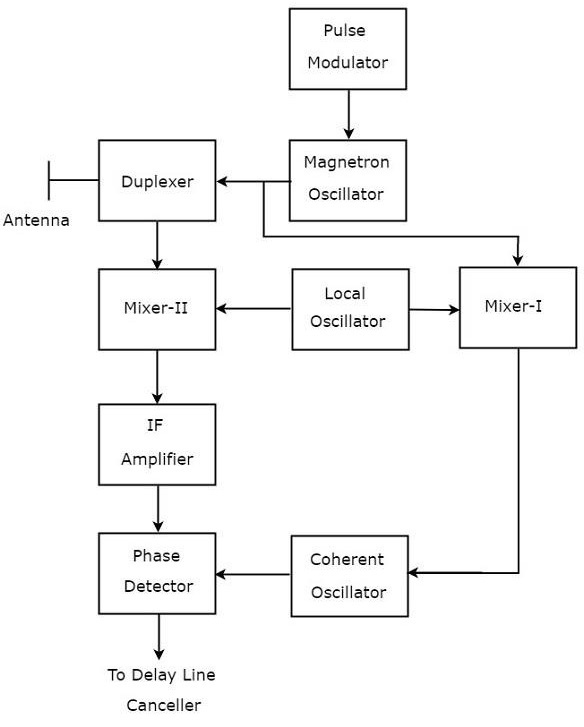
Блок-схема MTI Radar с передатчиком генератора мощности выглядит аналогично блок-схеме MTI Radar с передатчиком усилителя мощности. Блоки, соответствующие секции приемника, будут одинаковыми на обеих блок-схемах. Принимая во внимание, что блоки, соответствующие секции передатчика, могут отличаться на обеих блок-схемах.

Блок-схема MTI Radar с передатчиком мощности генератора показана на следующем рисунке.

Как показано на рисунке, MTI Radar использует единую антенну для передачи и приема сигналов с помощью дуплексера. Работа MTI Radar с передатчиком генератора мощности описана ниже.

• Выход магнетронного генератора и выход локального генератора подключены к микшеру-I. Это также будет генерировать сигнал ПЧ , фаза которого напрямую связана с фазой передаваемого сигнала.

• Выход Mixer-I подается на когерентный генератор. Следовательно, фаза выхода когерентного генератора будет привязана к фазе сигнала ПЧ. Это означает, что фаза выхода когерентного генератора также будет напрямую связана с фазой передаваемого сигнала.

• Таким образом, выходной сигнал когерентного генератора может быть использован в качестве опорного сигнала для сравнения принятого эхо — сигнала с соответствующим передаваемого сигнала с помощью фазового детектора.

Выход магнетронного генератора и выход локального генератора подключены к микшеру-I. Это также будет генерировать сигнал ПЧ , фаза которого напрямую связана с фазой передаваемого сигнала.

Выход Mixer-I подается на когерентный генератор. Следовательно, фаза выхода когерентного генератора будет привязана к фазе сигнала ПЧ. Это означает, что фаза выхода когерентного генератора также будет напрямую связана с фазой передаваемого сигнала.

Таким образом, выходной сигнал когерентного генератора может быть использован в качестве опорного сигнала для сравнения принятого эхо — сигнала с соответствующим передаваемого сигнала с помощью фазового детектора.

Вышеуказанные задачи будут повторяться для каждого вновь передаваемого сигнала.

Радарные системы — компенсаторы задержки линии

В этой главе мы узнаем о компенсаторах линии задержки в радиолокационных системах. Как следует из названия, линия задержки вводит определенную величину задержки. Таким образом, линия задержки в основном используется в компенсаторе линии задержки, чтобы ввести задержку времени повторения импульса.

Подавитель линии задержки представляет собой фильтр, который устраняет составляющие постоянного тока эхо-сигналов, полученных от стационарных целей. Это означает, что он допускает компоненты переменного тока эхо-сигналов, полученных от нестационарных целей, то есть движущихся целей.

Типы подавителей линии задержки

Компенсаторы линии задержки могут быть классифицированы на следующие два типа в зависимости от количества линий задержки, которые присутствуют в ней.

• Подавитель одиночной линии задержки
• Линейка с двойной задержкой

В наших последующих разделах мы обсудим больше об этих двух компенсаторах линии задержки.

Подавитель одиночной линии задержки

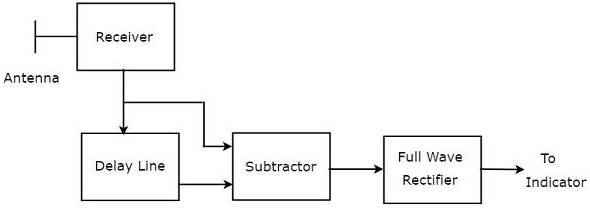
Комбинация линии задержки и вычитателя известна как компенсатор линии задержки. Это также называется однократной задержкой линии задержки. Блок-схема приемника MTI с одним подавителем линии задержки показана на рисунке ниже.

Мы можем записать математическое уравнение принятого эхо-сигнала после эффекта Доплера как —

$$V_1 = A \ sin \ left [2 \ pi f_dt- \ phi_0 \ right] \: \: \: \: \: Equation \: 1$$

Куда,

А — амплитуда видеосигнала

$f_d$ — доплеровская частота

$\ phi_o$ — фазовый сдвиг, он равен $4 \ pi f_tR_o / C$

Мы получим вывод средства подавления строки задержки , заменив $t$ на $t-T_P$ в уравнении 1.

$$V_2 = A \ sin \ left [2 \ pi f_d \ left (t-T_P \ right) - \ phi_0 \ right] \: \: \: \: \: Equation \: 2$$

Куда,

$T_P$ — время повторения импульсов

Мы получим результат вычитания путем вычитания уравнения 2 из уравнения 1.

$$V_1-V_2 = A \ sin \ left [2 \ pi f_dt- \ phi_0 \ right] -A \ sin \ left [2 \ pi f_d \ left (t-T_P \ right) - \ phi_0 \ right]$$

$$\ Rightarrow V_1-V_2 = 2A \ sin \ left [\ frac {2 \ pi f_dt- \ phi_0- \ left [2 \ pi f_d \ left (t-T_P \ right) - \ phi_0 \ right]} {2 } \ right] \ cos \ left [\ frac {2 \ pi f_dt- \ phi_o + 2 \ pi f_d \ left (t-T_P \ right) - \ phi_0} {2} \ right]$$

$$V_1-V_2 = 2A \ sin \ left [\ frac {2 \ pi f_dT_P} {2} \ right] \ cos \ left [\ frac {2 \ pi f_d \ left (2t-T_P \ right) -2 \ phi_0} {2} \ right]$$

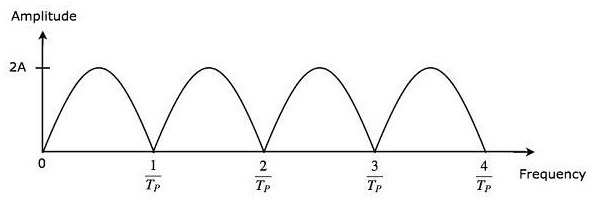
$$\ Rightarrow V_1-V_2 = 2A \ sin \ left [\ pi f_dT_p \ right] \ cos \ left [2 \ pi f_d \ left (t- \ frac {T_P} {2} \ right) - \ phi_0 \ right ] \: \: \: \: \: Уравнение \: 3$$

Выход вычитателя применяется как вход для выпрямителя полной волны. Таким образом, вывод выпрямителя Full Wave выглядит так, как показано на следующем рисунке. Это не что иное, как частотная характеристика подавителя линии задержки.

Из уравнения 3 мы можем наблюдать, что частотная характеристика средства подавления одиночной линии задержки становится равной нулю, когда $\ pi f_dT_P$ равно целому числу, кратному $\ pi$. Это означает, что $\ pi f_dT_P$ равно $n \ pi$ Математически это можно записать как

$$\ pi f_dT_P = n \ pi$$

$$\ Rightarrow f_dT_P = n$$

$$\ Rightarrow f_d = \ frac {n} {T_P} \: \: \: \: \: Уравнение \: 4$$

Из уравнения 4 можно сделать вывод, что частотная характеристика компенсатора одиночной линии задержки становится равной нулю, когда доплеровская частота $f_d$ равна целому числу, кратному обратной величине времени повторения импульса $T_P$.

Нам известно следующее соотношение между временем повторения импульса и частотой повторения импульса.

$$f_d = \ гидроразрыва {1} {T_P}$$

$$\ Rightarrow \ frac {1} {T_P} = f_P \: \: \: \: \: Equation \: 5$$

Мы получим следующее уравнение, подставив уравнение 5 в уравнение 4.

$$\ Rightarrow f_d = nf_P \: \: \: \: \: Equation \: 6$$

Из уравнения 6 можно сделать вывод, что частотная характеристика компенсатора одиночной линии задержки становится равной нулю, когда доплеровская частота, $f_d$, равна целым кратным частоты повторения импульсов $f_P$.

Слепые скорости

Из того, что мы узнали до сих пор, подавитель одиночной линии задержки устраняет компоненты постоянного тока эхо-сигналов, полученных от стационарных целей, когда $n$ равно нулю. В дополнение к этому он также устраняет компоненты переменного тока эхо-сигналов, принимаемых от нестационарных целей, когда доплеровская частота $f_d$ равна целым (отличным от нуля) кратным частоты повторения импульсов $f_P$.

Таким образом, относительные скорости, для которых частотная характеристика компенсатора одиночной линии задержки становится равной нулю, называются слепыми скоростями . Математически мы можем записать выражение для слепой скорости $v_n$ как —

$$V_n = \ гидроразрыва {п \ Lambda} {2T_P} \: \: \: \: \: Уравнение \: 7$$

$$\ Rightarrow v_n = \ frac {n \ lambda f_P} {2} \: \: \: \: \: Equation \: 8$$

Куда,

$n$ — это целое число, равное 1, 2, 3 и т. д.

$\ lambda$ — рабочая длина волны

Пример задачи

Радар MTI работает на частоте $6 ГГц с частотой повторения импульсов$ 1 КГц. Найдите первую, вторую и третью слепые скорости этого радара.

Решение

Дано,

Рабочая частота MTI Radar, $f = 6 ГГц$

Частота повторения импульсов, $ f_P = 1 кГц.

Ниже приведена формула для рабочей длины волны $\ lambda$ с точки зрения рабочей частоты, f.

$$\ Lambda = \ гидроразрыва {C}, {F}$$

Замените $C = 3 \ times10 ^ 8m / sec$ и $f = 6GHZ$ в вышеприведенном уравнении.

$$\ Lambda = \ гидроразрыва {3 \ times10 ^ 8} {6 \ times10 ^ 9}$$

$$\ Rightarrow \ lambda = 0,05м$$

Таким образом, рабочая длина волны $\ lambda$ равна $0,05 млн., Когда рабочая частота f составляет$ 6 ГГц.

Мы знаем следующую формулу для слепой скорости .

$$v_n = \ frac {n \ lambda f_p} {2}$$

Подставив $n$ = 1,2 & 3 в вышеприведенном уравнении, мы получим следующие уравнения для первой, второй и третьей скоростей блайндов соответственно.

$$v_1 = \ frac {1 \ times \ lambda f_p} {2} = \ frac {\ lambda f_p} {2}$$

$$v_2 = \ frac {2 \ times \ lambda f_p} {2} = 2 \ left (\ frac {\ lambda f_p} {2} \ right) = 2v_1$$

$$v_3 = \ frac {3 \ times \ lambda f_p} {2} = 3 \ left (\ frac {\ lambda f_p} {2} \ right) = 3v_1$$

Подставим значения $\ lambda$ и $f_P$ в уравнение первой слепой скорости.

$$v_1 = \ frac {0.05 \ times 10 ^ 3} {2}$$

$$\ Rightarrow v_1 = 25 м / с$$

Следовательно, первая слепая скорость $v_1$ для данных спецификаций равна $25m / sec$.

Мы получим значения второй и третьей скоростей блайндов как $50 м / с$ и $75 м / с$ соответственно, подставив значение ð ‘£ 1 в уравнения второй и третьей скоростей блайндов.

Линейка с двойной задержкой

Мы знаем, что один компенсатор строки задержки состоит из линии задержки и вычитателя. Если два таких компенсатора линии задержки каскадируются вместе, то эта комбинация называется Двойным компенсатором линии задержки. Блок-схема компенсатора линии двойной задержки показана на следующем рисунке.

Пусть $p \ left (t \ right)$ и $q \ left (t \ right)$ будут входом и выходом первого компенсатора линии задержки. Мы получим следующее математическое соотношение из первого компенсатора линии задержки .

$$q \ left (t \ right) = p \ left (t \ right) -p \ left (t-T_P \ right) \: \: \: \: \: Equation \: 9$$

Выход первого подавителя строки задержки применяется как вход для второго подавителя строки задержки. Следовательно, $q \ left (t \ right)$ будет входом второго компенсатора линии задержки. Пусть $r \ left (t \ right)$ будет выводом второго компенсатора линии задержки. Мы получим следующее математическое соотношение из второго компенсатора линии задержки .

$$r \ left (t \ right) = q \ left (t \ right) -q \ left (t-T_P \ right) \: \: \: \: \: Equation \: 10$$

Замените $t$ на $t-T_P$ в уравнении 9.

$$q \ left (t-T_P \ right) = p \ left (t-T_P \ right) -p \ left (t-T_P-T_P \ right)$$

$$q \ left (t-T_P \ right) = p \ left (t-T_P \ right) -p \ left (t-2T_P \ right) \: \: \: \: \: Уравнение \: 11$$

Замените уравнение 9 и уравнение 11 в уравнении 10.

$$r \ left (t \ right) = p \ left (t \ right) -p \ left (t-T_P \ right) - \ left [p \ left (t-T_P \ right) -p \ left (t -2T_P \ right) \ right]$$

$$\ Rightarrow r \ left (t \ right) = p \ left (t \ right) -2p \ left (t-T_P \ right) + p \ left (t-2T_P \ right) \: \: \: \ : \: Уравнение \: 12$$

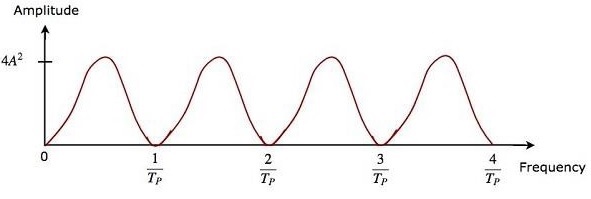
Преимущество двойной линии подавления задержки заключается в том, что она широко отвергает беспорядок. Выход двух компенсаторов линии задержки, которые расположены каскадно, будет равен квадрату выходного сигнала одного компенсатора линии задержки.

Таким образом, величина выходного сигнала компенсатора линии двойной задержки, присутствующего в приемнике MTI Radar, будет равна $4A ^ 2 \ left (\ sin \ left [\ pi f_dT_P \ right] \ right) ^ 2$.

Частотные характеристики как устройства подавления линии с двойной задержкой, так и каскадной комбинации двух устройств подавления линии с задержкой одинаковы. Преимущество подавителя линии задержки во временной области состоит в том, что он может работать для всех частотных диапазонов.

Радарные системы — Радар слежения

Радар, который используется для отслеживания пути одной или нескольких целей, известен как отслеживающий радар . Как правило, он выполняет следующие функции перед запуском отслеживания.

• Обнаружение цели
• Дальность цели
• Нахождение углов места и азимута
• Нахождение доплеровского сдвига частоты

Итак, Tracking Radar отслеживает цель, отслеживая один из трех параметров — диапазон, угол, доплеровский сдвиг частоты. Большинство радаров слежения используют принцип слежения под углом . Теперь давайте обсудим, что такое угловое отслеживание.

Угловое слежение

Лучи антенны радара следят за углом. Ось радиолокационной антенны считается опорным направлением. Если направление цели и опорного направления не совпадают, то будет угловая ошибка, которая не что иное, как разница между этими двумя направлениями.

Если сигнал угловой ошибки подается на систему сервоуправления, он перемещает ось радиолокационной антенны в направлении цели. Ось радиолокационной антенны и направление цели будут совпадать, когда угловая погрешность равна нулю. В радаре слежения существует механизм обратной связи, который работает до тех пор, пока угловая ошибка не станет равной нулю.

Ниже приведены два метода , которые используются в угловом слежении.

• Последовательный Lobing
• Коническое сканирование

Теперь давайте поговорим об этих двух методах один за другим.

Последовательный Lobing

Если лучи антенны переключаются между двумя схемами попеременно для отслеживания цели, то это называется последовательным распределением . Это также называется последовательным переключением и переключением лепестков. Этот метод используется, чтобы найти угловую ошибку в одной координате. Он дает подробную информацию о величине и направлении угловой ошибки.

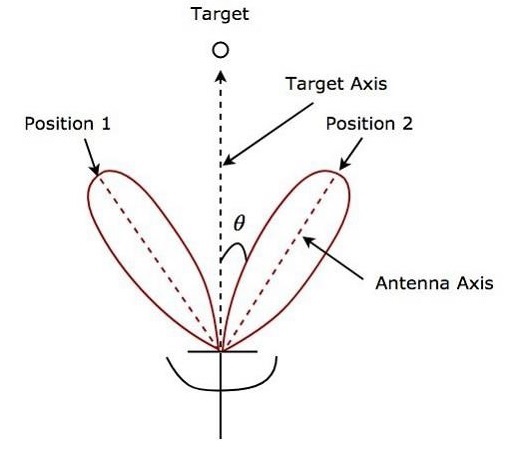
На следующем рисунке показан пример последовательного лепестка в полярных координатах .

Как показано на рисунке, лучи антенны попеременно переключаются между положением 1 и положением 2. Угловая ошибка θ указана на рисунке выше. Последовательный удар дает положение цели с высокой точностью. Это главное преимущество последовательного лоббирования.

Коническое сканирование

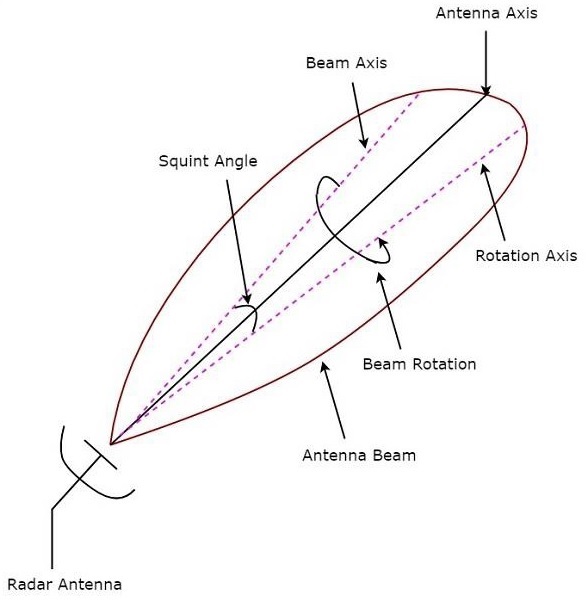
Если луч антенны постоянно вращается для отслеживания цели, то это называется коническим сканированием . Коническая модуляция сканирования используется, чтобы найти положение цели. На следующем рисунке показан пример конического сканирования.

Угол сквита — это угол между осью луча и осью вращения, он показан на рисунке выше. Эхо-сигнал, полученный от цели, модулируется на частоте, равной частоте, на которой вращается луч антенны.

Угол между направлением цели и осью вращения определяет амплитуду модулированного сигнала . Таким образом, модуляция конического сканирования должна быть извлечена из эхо-сигнала, а затем она должна быть применена к серво-системе управления, которая перемещает ось луча антенны в направлении цели.

Радарные системы — параметры антенны

Антенна или антенна — это преобразователь, который преобразует электрическую энергию в электромагнитные волны и наоборот.

Антенна имеет следующие параметры —

• направленность
• Эффективность диафрагмы
• Эффективность антенны
• Усиление

Теперь давайте обсудим эти параметры подробно —

направленность

Согласно стандартному определению, «отношение максимальной интенсивности излучения рассматриваемой Антенны к интенсивности излучения изотропной или эталонной Антенны, излучающей одинаковую общую мощность, называется Направленностью ».

Хотя антенна излучает энергию, направление, в котором она излучает, имеет большое значение. Исследуемая Антенна называется предметной Антенной . Его интенсивность излучения фокусируется в определенном направлении, когда он передает или принимает. Следовательно, антенна, как говорят, имеет свою направленность в этом конкретном направлении.

• Отношение интенсивности излучения в данном направлении от Антенны к интенсивности излучения, усредненной по всем направлениям, называется Направленностью .

• Если это конкретное направление не указано, то направление, в котором наблюдается максимальная интенсивность, может быть принято за направленность этой антенны.

• Направленность неизотропной антенны равна отношению интенсивности излучения в данном направлении к интенсивности излучения изотропного источника.

Отношение интенсивности излучения в данном направлении от Антенны к интенсивности излучения, усредненной по всем направлениям, называется Направленностью .

Если это конкретное направление не указано, то направление, в котором наблюдается максимальная интенсивность, может быть принято за направленность этой антенны.

Направленность неизотропной антенны равна отношению интенсивности излучения в данном направлении к интенсивности излучения изотропного источника.

Математически мы можем написать выражение для Направленности как —

$$Directivity = \ frac {U_ {Max} \ left (\ theta, \ phi \ right)} {U_0}$$

Куда,

$U_ {Max} \ left (\ theta, \ phi \ right)$ — максимальная интенсивность излучения антенны субъекта

$U_0$ — интенсивность излучения изотропной антенны.

Эффективность диафрагмы

Согласно стандартному определению, «эффективность апертуры антенны — это отношение эффективной излучающей площади (или эффективной площади) к физической площади апертуры».

Антенна излучает энергию через отверстие. Это излучение должно быть эффективным с минимальными потерями. Следует также учитывать физическую площадь апертуры, поскольку эффективность излучения зависит от площади апертуры, физически от антенны.

Математически мы можем записать выражение для эффективности апертуры $\ epsilon_A$ как

$$\ epsilon _A = \ frac {A_ {eff}} {A_p}$$

Куда,

$A_ {eff}$ — эффективная площадь

$A_P$ — физическая область

Эффективность антенны

Согласно стандартному определению, «Эффективность антенны — это отношение излучаемой мощности Антенны к потребляемой Антенной входной мощности».

Любая антенна предназначена для излучения мощности с минимальными потерями для данного входа. Эффективность Антенны объясняет, насколько Антенна способна эффективно доставлять свою мощность с минимальными потерями в линии передачи. Это также называется коэффициентом радиационной эффективности антенны.

Математически мы можем записать выражение для эффективности антенны ?? как —

$$\ eta _e = \ frac {P_ {Rad}} {P_ {in}}$$

Куда,

$P_ {Rad}$ — количество излучаемой мощности.

$P_ {in}$ — входная мощность для антенны

Усиление

Согласно стандартному определению, «усиление антенны — это отношение интенсивности излучения в данном направлении к интенсивности излучения, которая была бы получена, если бы мощность, принимаемая антенной, излучалась изотропно».

Проще говоря, усиление антенны учитывает направленность антенны наряду с ее эффективными характеристиками. Если мощность, принимаемая Антенной, излучалась изотропно (то есть во всех направлениях), то интенсивность излучения, которую мы получаем, может быть принята за эталонную.

• Термин усиление антенны описывает, сколько энергии передается в направлении пикового излучения на источник изотропного излучения.

• Усиление обычно измеряется в дБ .

• В отличие от направленности, усиление антенны учитывает также потери, которые возникают, и, следовательно, фокусируется на эффективности.

Термин усиление антенны описывает, сколько энергии передается в направлении пикового излучения на источник изотропного излучения.

Усиление обычно измеряется в дБ .

В отличие от направленности, усиление антенны учитывает также потери, которые возникают, и, следовательно, фокусируется на эффективности.

Математически мы можем записать выражение для Antenna Gain $G$ как —

$$G = \ eta_eD$$

Куда,

$\ eta_e$ — эффективность антенны

$D$ — Направленность Антенны

Радарные Системы — Радарные Антенны

В этой главе давайте узнаем об Антеннах, которые полезны в радиолокационной связи. Мы можем классифицировать радиолокационные антенны на следующие два типа в зависимости от физической структуры.

• Параболические рефлекторные антенны
• Объективные Антенны

В наших последующих разделах мы подробно обсудим два типа антенн.

Параболические рефлекторные антенны

Параболические рефлекторные антенны — это микроволновые антенны. Знание параболического рефлектора необходимо для глубокого понимания работы антенн.

Принцип действия

Парабола — это не что иное, как Локус точек, которые движутся таким образом, что его расстояние от фиксированной точки (называемой фокусом) плюс расстояние от прямой (называемой прямой) является постоянным.

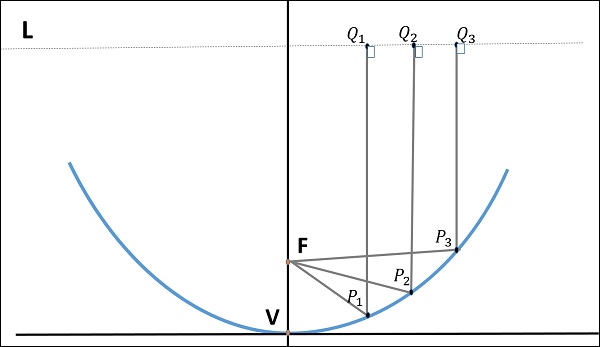
На следующем рисунке показана геометрия параболического отражателя . Точки F и V — фокус (подача дана) и вершина соответственно. Линия, соединяющая F и V, является осью симметрии. $P_1Q_1, P_2Q_2$ и $P_3Q_3$ являются отраженными лучами. Линия L представляет директрису, на которой лежат отраженные точки (чтобы сказать, что они коллинеарны).

Как показано на рисунке, расстояние между F и L является постоянным по отношению к фокусируемым волнам. Отраженная волна образует коллимированный волновой фронт из параболической формы. Отношение фокусного расстояния к размеру апертуры (то есть, $f / D$) известно как «отношение f к D» . Это важный параметр параболического отражателя, и его значение варьируется от 0,25 до 0,50 .

Закон отражения гласит, что угол падения и угол отражения равны. Этот закон при использовании вместе с параболой помогает фокусировать луч. Форма параболы, когда она используется для отражения волн, обладает некоторыми свойствами параболы, которые полезны для построения антенны с использованием отраженных волн.

Свойства Параболы

Ниже приведены различные свойства Parabola —

• Все волны, исходящие из фокуса, отражаются обратно к параболической оси. Следовательно, все волны, достигающие апертуры, находятся в фазе.

• Поскольку волны находятся в фазе, луч излучения вдоль параболической оси будет сильным и концентрированным.

Все волны, исходящие из фокуса, отражаются обратно к параболической оси. Следовательно, все волны, достигающие апертуры, находятся в фазе.

Поскольку волны находятся в фазе, луч излучения вдоль параболической оси будет сильным и концентрированным.

Следуя этим пунктам, параболические отражатели помогают создавать высокую направленность при более узкой ширине луча.

Конструкция и работа параболического отражателя

Если параболический отражатель антенна используется для передачи сигнала, сигнал из канала выходит из дипольной антенны или рупорной антенну, чтобы сфокусировать волну на параболу. Это означает, что волны выходят из фокальной точки и ударяются о параболоидный отражатель. Эта волна теперь отражается как коллимированный фронт волны, как обсуждалось ранее, для передачи.

Та же антенна используется в качестве приемника . Когда электромагнитная волна принимает форму параболы, она отражается в точке подачи. Дипольная антенна или рупорная антенна, которая действует как приемная антенна при подаче, получает этот сигнал, чтобы преобразовать его в электрический сигнал и направить его в схему приемника.

Коэффициент усиления параболоида является функцией отношения апертуры $D / \ lambda$. Эффективная излучаемая мощность (ERP) антенны — это умножение входной мощности, подаваемой на антенну, и ее усиления.

Обычно антенна для волноводного рупора используется в качестве радиатора питания для антенны параболоидного отражателя. Наряду с этой техникой, у нас есть следующие два типа подачи данных на антенну параболоидного отражателя.

• Кассегрена
• Григорианский канал

Кассегрена

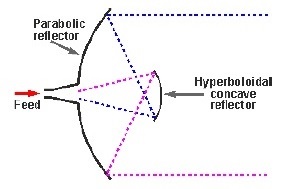
В этом типе подача расположена в вершине параболоида, в отличие от параболического отражателя. Отражатель выпуклой формы, который действует как гиперболоид, расположен напротив источника питания антенны. Он также известен как вторичный гиперболоидный рефлектор или субрефлектор. Он расположен таким образом, что один из его фокусов совпадает с фокусом параболоида. Таким образом, волна отражается дважды.

На приведенном выше рисунке показана рабочая модель корма для запеканки.

Григорианский канал

Тип подачи, где есть пара определенных конфигураций и где ширина луча подачи постепенно увеличивается, в то время как размеры антенны остаются фиксированными, называется григорианской подачей . Здесь гиперболоид выпуклой формы Кассегрена заменяется параболоидным отражателем вогнутой формы, который, конечно, меньше по размеру.

Эти отражатели григорианского типа подачи могут быть использованы следующими четырьмя способами:

• Григорианские системы с использованием эллипсоидального субрефлектора отражателя в фокусах F1.

• Григорианские системы, использующие эллипсоидальный субрефлектор отражателя в фокусах F2.

• Системы Кассегрена, использующие гиперболоидный суботражатель (выпуклый).

• Системы Кассегрена, использующие гиперболоидный суботражатель (вогнутый, но подача очень близко к нему)

Григорианские системы с использованием эллипсоидального субрефлектора отражателя в фокусах F1.

Григорианские системы, использующие эллипсоидальный субрефлектор отражателя в фокусах F2.

Системы Кассегрена, использующие гиперболоидный суботражатель (выпуклый).

Системы Кассегрена, использующие гиперболоидный суботражатель (вогнутый, но подача очень близко к нему)

Среди различных типов отражательных антенн наиболее часто используются простые параболические отражатели и параболические отражатели подачи Кассегрена.

Объективные Антенны

Объективные антенны используют изогнутую поверхность как для передачи, так и для приема сигналов. Эти антенны сделаны из стекла, где соблюдаются сходящиеся и расходящиеся свойства линзы. Частотный диапазон использования Lens Antenna начинается с 1 ГГц, но его использование больше на 3 ГГц и выше .

Знание объектива необходимо для глубокого понимания работы антенны объектива. Напомним, что обычная стеклянная линза работает по принципу преломления .

Конструкция и работа линзовой антенны

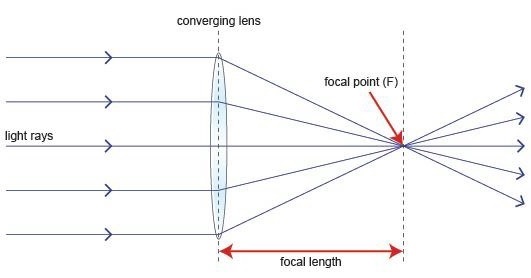
Если предполагается, что источник света присутствует в фокусной точке линзы, которая находится на фокусном расстоянии от объектива, то лучи проходят через объектив в виде коллимированных или параллельных лучей на плоском фронте волны.

Есть два явления, которые происходят, когда лучи падают с разных сторон линзы. Они даны здесь —

• Лучи, которые проходят через центр линзы, менее преломлены, чем лучи, которые проходят через края линзы. Все лучи направляются параллельно плоскому фронту волны. Этот феномен объектива называется расхождением .

• Та же самая процедура становится обратной, если луч света посылается с правой стороны на левую сторону того же объектива. Затем луч преломляется и встречается в точке, называемой фокусной точкой, на фокусном расстоянии от линзы. Это явление называется конвергенцией .

Лучи, которые проходят через центр линзы, менее преломлены, чем лучи, которые проходят через края линзы. Все лучи направляются параллельно плоскому фронту волны. Этот феномен объектива называется расхождением .

Та же самая процедура становится обратной, если луч света посылается с правой стороны на левую сторону того же объектива. Затем луч преломляется и встречается в точке, называемой фокусной точкой, на фокусном расстоянии от линзы. Это явление называется конвергенцией .

Следующая диаграмма поможет нам лучше понять это явление.

Диаграмма луча представляет фокус и фокусное расстояние от источника до объектива. Полученные параллельные лучи также называют коллимированными лучами.

На приведенном выше рисунке источник в фокусе, на фокусном расстоянии от объектива, коллимируется во фронте плоской волны. Это явление можно обратить вспять, что означает, что свет, если он посылается с левой стороны, сходится на правой стороне объектива.

Именно из-за этой взаимности Линза может использоваться в качестве Антенны, поскольку одно и то же явление помогает использовать одну и ту же Антенну как для передачи, так и для приема.

Для достижения фокусирующих свойств на более высоких частотах показатель преломления должен быть меньше единицы. Каким бы ни был показатель преломления, целью линзы является выпрямление формы волны. На основании этого разработаны объективы E-плоскости и H-плоскости, которые также задерживают или ускоряют волновой фронт.

Радарные системы — приемник согласованного фильтра

Если фильтр производит выходной сигнал таким образом, что он максимизирует отношение пиковой выходной мощности к средней мощности шума в своей частотной характеристике, тогда этот фильтр называется согласованным фильтром .

Это важный критерий, который учитывается при проектировании любого радиолокационного приемника. В этой главе мы обсудим функцию частотной характеристики согласованного фильтра и импульсную характеристику согласованного фильтра.

Функция частотного отклика согласованного фильтра

Частотная характеристика согласованного фильтра будет пропорциональна комплексному сопряжению спектра входного сигнала. Математически мы можем записать выражение для функции АЧХ , $H \ left (f \ right)$ фильтра Matched, как —

$$H \ left (f \ right) = G_aS ^ \ ast \ left (f \ right) e ^ {- j2 \ pi ft_1} \: \: \: \: \: Equation \: 1$$

Куда,

$G_a$ — максимальное усиление фильтра Matched

$S \ left (f \ right)$ — преобразование Фурье входного сигнала, $s \ left (t \ right)$

$S ^ \ ast \ left (f \ right)$ — комплексное сопряжение $S \ left (f \ right)$

$t_1$ — момент времени, в который наблюдаемый сигнал является максимальным

В общем случае значение $G_a$ считается единым. Мы получим следующее уравнение, подставив $G_a = 1$ в уравнение 1.

$$H \ left (f \ right) = S ^ \ ast \ left (f \ right) e ^ {- j2 \ pi ft_1} \: \: \: \: \: Equation \: 2$$

Функция частотной характеристики $H \ left (f \ right)$ фильтра Matched имеет величину $S ^ \ ast \ left (f \ right)$ и фазовый угол $e ^ {- j2 \ pi ft_1 }$, который меняется равномерно с частотой.

Импульсный отклик согласованного фильтра

Во временной области мы получим выходной сигнал $h (t)$ приемника согласованного фильтра, применив обратное преобразование Фурье функции АЧХ $H (f)$.

$$h \ left (t \ right) = \ int _ {- \ infty} ^ {\ infty} H \ left (f \ right) e ^ {- j2 \ pi ft_1} df \: \: \: \: \ : Уравнение \: 3$$

Заменить уравнение 1 в уравнении 3.

$$h \ left (t \ right) = \ int _ {- \ infty} ^ {\ infty} \ lbrace G_aS ^ \ ast \ left (f \ right) e ^ {- j2 \ pi ft_1} \ rbrace e ^ { j2 \ pi ft} df$$

$$\ Rightarrow h \ left (t \ right) = \ int _ {- \ infty} ^ {\ infty} G_aS ^ \ ast \ left (f \ right) e ^ {- j2 \ pi f \ left (t_1-t \ right)} df \: \: \: \: \: Equation \: 4$$

Мы знаем следующее соотношение.

$$S ^ \ ast \ left (f \ right) = S \ left (-f \ right) \: \: \: \: \: Equation \: 5$$

Замените уравнение 5 на уравнение 4.

$$h \ left (t \ right) = \ int _ {- \ infty} ^ {\ infty} G_aS (-f) e ^ {- j2 \ pi f \ left (t_1-t \ right)} df$$

$$\ Rightarrow h \ left (t \ right) = \ int _ {- \ infty} ^ {\ infty} G_aS ^ \ left (f \ right) e ^ {j2 \ pi f \ left (t_1-t \ right) } ДФ$$

$$\ Rightarrow h \ left (t \ right) = G_as (t_1 − t) \: \: \: \: \: Уравнение \: 6$$

В общем случае значение $G_a$ считается единым. Мы получим следующее уравнение, подставив $G_a = 1$ в уравнение 6.

$$h (t) = s \ left (t_1-t \ right)$$

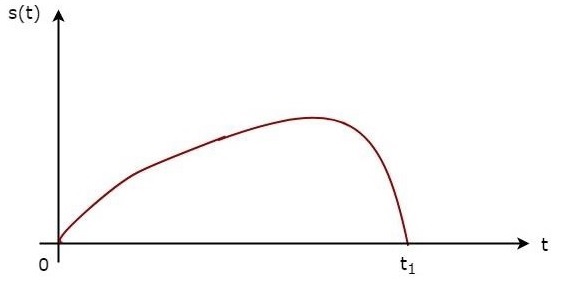
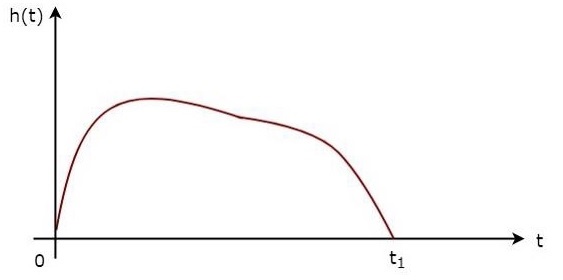
Вышеупомянутое уравнение доказывает, что импульсный отклик согласованного фильтра является зеркальным отражением принятого сигнала в момент времени $t_1$. Следующие рисунки иллюстрируют эту концепцию.

Полученный сигнал, $s \ left (t \ right)$ и импульсный отклик, $h \ left (t \ right)$ согласованного фильтра, соответствующего сигналу, $s \ left (t \ right)$, показаны на приведенных выше рисунках.

Радарные системы — Радарные дисплеи

Электронный инструмент, который используется для визуального отображения данных, называется дисплеем. Таким образом, электронный инструмент, который отображает информацию о цели радара визуально, называется дисплеем радара . Он отображает информацию о эхо-сигнале визуально на экране.

Типы радарных дисплеев

В этом разделе мы узнаем о различных типах радарных дисплеев. Радарные дисплеи могут быть классифицированы на следующие типы.

A-Scope

Это двухмерный радарный дисплей. Горизонтальные и вертикальные координаты представляют диапазон и амплитуду эхо-сигнала цели соответственно. В A-Scope имеет место модуляция отклонения. Это больше подходит для ручного слежения за радаром .

Индикатор азимут-дальность

Это двухмерный радарный дисплей. Горизонтальные и вертикальные координаты представляют азимутальный угол и дальность цели соответственно. В B-Scope происходит модуляция интенсивности. Это больше подходит для военных радаров .

Индикатор типа с

Это двумерный радарный дисплей. Горизонтальные и вертикальные координаты представляют угол азимута и угол места соответственно. В C-Scope имеет место модуляция интенсивности.

D-Scope

Если электронный луч отклонен или на дисплее радара появляется пятно, модулированное по интенсивности, из-за присутствия цели, то это называется вспышкой. C-Scope становится D-Scope, когда блики проходят вертикально, чтобы обеспечить расстояние.

E-Scope

Это двумерный радарный дисплей. Горизонтальные и вертикальные координаты представляют расстояние и угол места соответственно. В E-Scope происходит модуляция интенсивности.

F-Scope

Если радиолокационная антенна нацелена на цель, то F-Scope отображает цель в виде централизованного сообщения. Таким образом, горизонтальные и вертикальные смещения блика представляют горизонтальные и вертикальные ошибки прицеливания соответственно.

G-Scope

Если радиолокационная антенна нацелена на цель, то G-Scope отображает цель как боковое централизованное сообщение. Горизонтальные и вертикальные смещения блика представляют ошибки горизонтального и вертикального прицеливания соответственно.

H-Scope

Это модифицированная версия B-Scope для предоставления информации об угле места цели. Он отображает цель в виде двух бликов, которые расположены близко друг к другу. Это может быть приближено к короткой яркой линии, и наклон этой линии будет пропорционален синусу угла места.

I-Scope

Если радиолокационная антенна нацелена на цель, то I-Scope отображает цель в виде круга . Радиус этого круга будет пропорционален расстоянию до цели. Если радарная антенна нацелена на цель неправильно, то I-Scope отображает цель в виде сегмента, а не круга. Длина дуги этого сегмента будет обратно пропорциональна величине ошибки наведения.

J-Сфера

Это модифицированная версия A-Scope. Он отображает цель как радиальное отклонение от временной базы.

K-Scope

Это модифицированная версия A-Scope. Если радиолокационная антенна направлена ​​на цель, то K-Scope отображает цель в виде пары вертикальных отклонений, имеющих одинаковую высоту. Если радарная антенна нацелена на цель неправильно, то будет ошибка наведения. Таким образом, величина и направление ошибки наведения зависят от разницы между двумя вертикальными отклонениями.

L-Scope

Если радиолокационная антенна направлена ​​на цель, то L-Scope отображает цель в виде двух горизонтальных вспышек, имеющих одинаковую амплитуду. Один горизонтальный всплеск лежит справа от центральной вертикальной временной шкалы, а другой — слева от центральной вертикальной временной шкалы.

M-Scope

Это модифицированная версия A-Scope. Регулируемый сигнал пьедестала должен перемещаться вдоль базовой линии, пока он не совпадет с отклонениями сигнала, исходящими из горизонтального положения цели. Таким образом, расстояние цели может быть определено.

N-Scope

Это модифицированная версия K-Scope. Регулируемый сигнал пьедестала используется для измерения расстояния.

O-Scope

Это модифицированная версия A-Scope. Мы получим O-Scope, включая регулируемую насечку для A-Scope для измерения расстояния.

P-Scope

Это дисплей радара, который использует модуляцию интенсивности. Он отображает информацию о эхо-сигнале в виде плана. Диапазон и угол азимута отображаются в полярных координатах. Следовательно, он называется индикатором положения плана или дисплеем PPI .

R-Scope

Это дисплей радара, который использует модуляцию интенсивности. Горизонтальные и вертикальные координаты представляют диапазон и высоту цели соответственно. Следовательно, это называется индикатором Range-Height или RHI .

Радарные Системы — Дуплексеры

При двусторонней связи, если мы должны использовать одну и ту же Антенну для передачи и приема сигналов, нам необходим дуплексер. Дуплексер — это микроволновый переключатель, который подключает антенну к секции передатчика для передачи сигнала. Поэтому радар не может получить сигнал во время передачи.

Аналогичным образом он подключает антенну к секции приемника для приема сигнала. Радар не может передавать сигнал во время приема. Таким образом, дуплексер изолирует секции передатчика и приемника.

Типы дуплексеров

В этом разделе мы узнаем о различных типах дуплексеров. Мы можем классифицировать дуплексеры по следующим трем типам .

• Дуплексер ответвительного типа
• Сбалансированный дуплексер
• Циркулятор как дуплексер

В наших последующих разделах мы подробно обсудим типы дуплексеров.

Дуплексер ответвительного типа

Дуплексер ответвительного типа состоит из двух коммутаторов — коммутатора Transmit-Receive (TR) и Anti-Transmit-Receive (ATR). На следующем рисунке показана блок-схема дуплексера типа Branch —

Как показано на рисунке, два переключателя TR & ATR расположены на расстоянии $\ lambda / 4$ от линии передачи, и оба переключателя разделены расстоянием $\ lambda / 4$. Работа дуплексера типа Branch упомянута ниже.

• Во время передачи оба TR & ATR будут выглядеть как разомкнутая цепь от линии передачи. Следовательно, антенна будет подключена к передатчику через линию передачи.

• Во время приема ATR будет выглядеть как короткое замыкание по линии передачи. Следовательно, антенна будет подключена к приемнику через линию передачи.

Во время передачи оба TR & ATR будут выглядеть как разомкнутая цепь от линии передачи. Следовательно, антенна будет подключена к передатчику через линию передачи.

Во время приема ATR будет выглядеть как короткое замыкание по линии передачи. Следовательно, антенна будет подключена к приемнику через линию передачи.

Дуплексер ответвительного типа подходит только для недорогих радаров, так как он имеет меньшую пропускную способность.

Сбалансированный дуплексер

Мы знаем, что направленный ответвитель с двумя отверстиями — это четырехпроводное волноводное соединение, состоящее из первичного волновода и вторичного волновода. Есть два небольших отверстия, которые будут общими для этих двух волноводов.

Сбалансированный дуплексер состоит из двух трубок TR. Конфигурация симметричного дуплексера для передачи показана на следующем рисунке.

Сигнал, который генерируется передатчиком, должен достигать Антенны, чтобы Антенна передавала этот сигнал во время передачи. Сплошные линии со стрелками, показанные на рисунке выше, показывают, как сигнал достигает антенны от передатчика.

Пунктирные линии со стрелками, показанные на рисунке выше, представляют сигнал, который вытекает из труб Dual TR; это достигнет только соответствующей нагрузки. Таким образом, сигнал не был получен для приемника.

Конфигурация сбалансированного дуплексера для цели приема показана на рисунке ниже.

Мы знаем, что антенна получает сигнал во время приема. Сигнал, который получает Антенна, должен достичь приемника. Сплошные линии со стрелками, показанные на рисунке выше, показывают, как сигнал достигает приемника от антенны. В этом случае трубки Dual TR пропускают сигнал от первого участка волновода к следующему участку волновода.

Сбалансированный дуплексер обладает высокой мощностью обработки и высокой пропускной способностью по сравнению с дуплексером типа филиала.

Циркулятор как дуплексер

Мы знаем, что функциональность циркулятора заключается в том, что если мы применяем вход к порту, то он будет создаваться в порту, который примыкает к нему по часовой стрелке. На остальных портах циркулятора нет выхода.

Итак, рассмотрим 4-портовый циркулятор и подключите передатчик, антенну, приемник и согласованную нагрузку к портам 1, 2, 3 и 4 соответственно. Теперь давайте разберемся, как 4-портовый циркулятор работает как дуплексер.

Сигнал, который генерирует передатчик, должен достигать Антенны, поскольку Антенна будет передавать этот сигнал в течение времени передачи . Эта цель будет достигнута, когда передатчик генерирует сигнал на порту 1.

Сигнал, который получает Антенна, должен достигать приемника во время приема . Эта цель будет достигнута, когда антенна, присутствующая в порту 2, получит внешний сигнал.

На следующем рисунке показана блок-схема циркулятора в качестве дуплексера —

На приведенном выше рисунке представлен 4-портовый циркулятор — передатчик, антенна, и согласованная нагрузка подключается к портам 1, 2 и 4 циркулятора соответственно, как обсуждалось в начале раздела.

Приемник не подключен напрямую к порту 3. Вместо этого блоки, соответствующие пассивному ограничителю TR, размещаются между портом 3 циркулятора и приемником. Блоки, трубка TR и диодный ограничитель являются блоками, соответствующими пассивному ограничителю TR.

Собственно, сам циркулятор действует как дуплексер. Не требует никаких дополнительных блоков. Тем не менее, это не даст никакой защиты приемнику. Следовательно, блоки, соответствующие пассивному ограничителю TR, используются для обеспечения защиты приемника .

Радарные системы — фазированные антенные решетки

Одна антенна может излучать определенное количество энергии в определенном направлении. Очевидно, что количество мощности излучения будет увеличено, когда мы будем использовать группу антенн вместе. Группа антенн называется антенной решеткой .

Антенная решетка — это излучающая система, состоящая из радиаторов и элементов. Каждый из этих излучателей имеет свое индукционное поле. Элементы расположены так близко, что каждый лежит в индукционном поле соседнего. Следовательно, диаграмма излучения, создаваемая ими, будет векторной суммой отдельных.

Антенны излучают индивидуально, и, когда они расположены в массиве, излучение всех элементов суммируется, чтобы сформировать луч излучения, который имеет высокий коэффициент усиления, высокую направленность и лучшую производительность с минимальными потерями.

Антенная решетка называется фазированной антенной решеткой, если форма и направление диаграммы направленности зависит от относительных фаз и амплитуд токов, присутствующих в каждой антенне этой решетки.

Радиационная картина

Рассмотрим «n» изотропных элементов излучения, которые при объединении образуют массив . Приведенный ниже рисунок поможет вам понять то же самое. Пусть интервал между последовательными элементами будет единицами ‘d’.

Как показано на рисунке, все излучающие элементы получают одинаковый входящий сигнал. Таким образом, каждый элемент выдает равное выходное напряжение $sin \ left (\ omega t \ right)$. Однако между последовательными элементами будет одинаковая разность фаз $\ Psi$. Математически это можно записать как —

$$\ Psi = \ frac {2 \ pi d \ sin \ theta} {\ lambda} \: \: \: \: \: Equation \: 1$$

Куда,

$\ theta$ — это угол, под которым входящий сигнал падает на каждый элемент излучения.

Математически мы можем записать выражения для выходных напряжений ‘n’ элементов излучения индивидуально как

$$E_1 = \ sin \ left [\ omega t \ right]$$

$$E_2 = \ sin \ left [\ omega t + \ Psi \ right]$$

$$E_3 = \ sin \ left [\ omega t + 2 \ Psi \ right]$$

.

.

.

$$E_n = \ sin \ left [\ omega t + \ left (N-1 \ right) \ Psi \ right]$$

Куда,

$E_1, E_2, E_3,…, E_n$ — выходные напряжения первого, второго, третьего,…, n- ^го излучающих элементов соответственно.

$\ omega$ — угловая частота сигнала.

Мы получим общее выходное напряжение массива $E_a$ путем сложения выходных напряжений каждого элемента, присутствующего в этом массиве, поскольку все эти излучающие элементы соединены в линейный массив. Математически это можно представить как —

$$E_a = E_1 + E_2 + E_3 +… + E_n \: \: \: Уравнение \: 2$$

Подставим значения $E_1, E_2, E_3,…, E_n$ в уравнение 2.

$$E_a = \ sin \ left [\ omega t \ right] + \ sin \ left [\ omega t + \ Psi \ right] + \ sin \ left [\ omega t + 2 \ Psi \ right] + \ sin \ left [\ omega t + \ left (n-1 \ right) \ Psi \ right]$$

$$\ Rightarrow E_a = \ sin \ left [\ omega t + \ frac {(n-1) \ Psi)} {2} \ right] \ frac {\ sin \ left [\ frac {n \ Psi} {2} \ right]} {\ sin \ left [\ frac {\ Psi} {2} \ right]} \: \: \: \: \: Equation \: 3$$

В уравнении 3 есть два условия. Из первого слагаемого мы можем наблюдать, что общее выходное напряжение $E_a$ является синусоидальной волной, имеющей угловую частоту $\ omega$. Но он имеет фазовый сдвиг $\ left (n − 1 \ right) \ Psi / 2$. Второе слагаемое в уравнении 3 является амплитудным фактором .

Величина уравнения 3 будет

$$ \ left | E_a \ right | = \ left | \ frac {\ sin \ left [\ frac {n \ Psi} {2} \ right]} {\ sin \ left [\ frac {\ Psi} {2} \ right]} \ right | \: \: \: \: \: Уравнение \: 4 $$

Мы получим следующее уравнение, подставив уравнение 1 в уравнение 4.

$$ \ left | E_a \ right | = \ left | \ frac {\ sin \ left [\ frac {n \ pi d \ sin \ theta} {\ lambda} \ right]} {\ sin \ left [\ frac {\ pi d \ sin \ theta} {\ lambda} \ right]} \ right | \: \: \: \: \: Equation \: 5 $$

Уравнение 5 называется диаграммой напряженности поля . Шаблон напряженности поля будет иметь значения нулей, когда числитель уравнения 5 равен нулю

$$\ sin \ left [\ frac {n \ pi d \ sin \ theta} {\ lambda} \ right] = 0$$

$$\ Rightarrow \ frac {n \ pi d \ sin \ theta} {\ lambda} = \ pm m \ pi$$

$$\ Rightarrow nd \ sin \ theta = \ pm m \ lambda$$

$$\ Rightarrow \ sin \ theta = \ pm \ frac {m \ lambda} {nd}$$

Куда,

$m$ — это целое число, равное 1, 2, 3 и т. д.

Мы можем найти максимальные значения модели напряженности поля, используя правило L-Hospital, когда числитель и знаменатель уравнения 5 равны нулю. Мы можем наблюдать, что если знаменатель уравнения 5 становится равным нулю, то числитель уравнения 5 также становится равным нулю.

Теперь давайте получим условие, при котором знаменатель уравнения 5 становится равным нулю.

$$\ sin \ left [\ frac {\ pi d \ sin \ theta} {\ lambda} \ right] = 0$$

$$\ Rightarrow \ frac {\ pi d \ sin \ theta} {\ lambda} = \ pm p \ pi$$

$$\ Rightarrow d \ sin \ theta = \ pm p \ lambda$$

$$\ Rightarrow \ sin \ theta = \ pm \ frac {p \ lambda} {d}$$

Куда,

$p$ — это целое число, равное 0, 1, 2, 3 и т. д.

Если мы рассмотрим $p$ как ноль, то получим значение $\ sin \ theta$ как ноль. Для этого случая мы получим максимальное значение диаграммы напряженности поля, соответствующее главному лепестку . Мы получим максимальные значения картины напряженности поля, соответствующие боковым лепесткам , когда рассмотрим другие значения $p$.

Направление диаграммы направленности фазированной решетки можно регулировать, изменяя относительные фазы тока, присутствующего в каждой антенне. В этом преимущество электронного сканирования фазированной решетки.