Факторы, которые влияют на производительность радара, известны как факторы производительности радара. В этой главе давайте поговорим об этих факторах. Мы знаем, что приведена следующая стандартная форма уравнения дальности радара, которая полезна для расчета максимальной дальности радара для заданных спецификаций.
$$ R_ {Max} = \ left [\ frac {P_tG \ sigma A_e} {\ left (4 \ pi \ right) ^ 2 S_ {min}} \ right] ^ {1/4} $$
Куда,
$ P_t $ — пиковая мощность, передаваемая радаром
$ G $ — усиление передающей антенны
$ \ sigma $ — радиолокационное сечение цели
$ A_e $ — эффективная апертура принимающей антенны
$ S_ {min} $ — мощность минимального обнаруживаемого сигнала
Из приведенного выше уравнения можно сделать вывод, что для получения максимальной дальности действия радара следует учитывать следующие условия .
- Пиковая мощность, передаваемая радаром $ P_t $, должна быть высокой.
- Усиление передающей антенны $ G $ должно быть высоким.
- Радиолокационное сечение цели $ \ sigma $ должно быть высоким.
- Эффективная апертура приемной антенны $ A_e $ должна быть высокой.
- Мощность минимально детектируемого сигнала $ S_ {min} $ должна быть низкой.
Трудно предсказать дальность цели из стандартной формы уравнения дальности радара. Это означает, что степень точности, которая обеспечивается уравнением радиолокационного диапазона относительно дальности цели, меньше. Потому что такие параметры, как сечение цели радара, $ \ sigma $ и минимально обнаруживаемый сигнал $ S_ {min} $, являются статистическими по своему характеру .
Минимальный обнаруживаемый сигнал
Если эхо-сигнал имеет минимальную мощность, обнаружение этого сигнала с помощью радара называется минимальным обнаруживаемым сигналом . Это означает, что радар не может обнаружить эхо-сигнал, если этот сигнал имеет меньшую мощность, чем сигнал минимальной мощности.
В общем, радар получает эхо-сигнал в дополнение к шуму. Если пороговое значение используется для обнаружения присутствия цели из принятого сигнала, то это обнаружение называется пороговым обнаружением .
Мы должны выбрать правильное пороговое значение в зависимости от силы сигнала, который будет обнаружен.
-
Высокое пороговое значение следует выбирать, когда интенсивность обнаруживаемого сигнала высока, чтобы исключить присутствующий в нем нежелательный шумовой сигнал.
-
Аналогично, низкое пороговое значение следует выбирать, когда сила обнаруживаемого сигнала низкая.
Высокое пороговое значение следует выбирать, когда интенсивность обнаруживаемого сигнала высока, чтобы исключить присутствующий в нем нежелательный шумовой сигнал.
Аналогично, низкое пороговое значение следует выбирать, когда сила обнаруживаемого сигнала низкая.
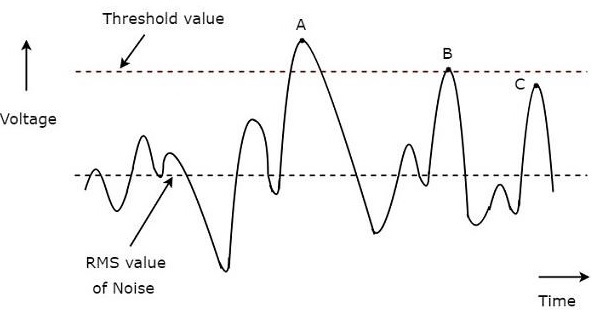
Следующий рисунок иллюстрирует эту концепцию —
Типичная форма сигнала радарного приемника показана на рисунке выше. Ось X и Y представляют время и напряжение соответственно. Среднеквадратичное значение шума и пороговое значение указаны пунктирными линиями на рисунке выше.
Мы рассмотрели три пункта, A, B и C на рисунке выше, для определения допустимых обнаружений и пропущенных обнаружений.
-
Значение сигнала в точке A превышает пороговое значение. Следовательно, это действительное обнаружение .
-
Значение сигнала в точке B равно пороговому значению. Следовательно, это действительное обнаружение .
-
Даже если значение сигнала в точке C ближе к пороговому значению, это пропущенное обнаружение . Потому что значение сигнала в точке C меньше порогового значения.
Значение сигнала в точке A превышает пороговое значение. Следовательно, это действительное обнаружение .
Значение сигнала в точке B равно пороговому значению. Следовательно, это действительное обнаружение .
Даже если значение сигнала в точке C ближе к пороговому значению, это пропущенное обнаружение . Потому что значение сигнала в точке C меньше порогового значения.
Таким образом, точки A и B являются действительными обнаружениями. Принимая во внимание, что точка C является отсутствующим обнаружением.
Шум приемника
Если приемник генерирует шумовую составляющую в сигнале, который принимается в приемнике, то этот вид шума называется шумом приемника. Шум приемника является нежелательным компонентом; мы должны попытаться устранить это с некоторыми мерами предосторожности.
Однако существует один вид шума, известный как тепловой шум. Это происходит из-за теплового движения электронов проводимости. Математически мы можем записать мощность теплового шума , $ N_i $, полученную на приемнике, как —
$$ N_i = KT_oB_n $$
Куда,
$ K $ — постоянная Больцмана, и она равна $ 1.38 \ times 10 ^ {- 23} Дж / град. $
$ T_o $ — абсолютная температура, равная $ 290 ^ 0K $
$ B_n $ — ширина полосы приемника
Фигура заслуги
Показатель заслуг , F — это не что иное, как отношение входного SNR, $ (SNR) _i $ и выходного SNR, $ (SNR) _o $. Математически это можно представить как —
$$ F = \ {гидроразрыва (SNR),-i} {(SNR), _o} $$
$$ \ Rightarrow F = \ frac {S_i / N_i} {S_o / N_o} $$
$$ \ Rightarrow F = \ frac {N_oS_i} {N_iS_o} $$
$$ \ Rightarrow S_i = \ frac {FN_iS_o} {N_o} $$
Замените $ N_i = KT_oB_n $ в приведенном выше уравнении.
$$ \ Rightarrow S_i = FKT_oB_n \ left (\ frac {S_o} {N_o} \ right) $$
Мощность входного сигнала будет иметь минимальное значение, когда выходное SNR имеет минимальное значение.
$$ \ Rightarrow S_ {min} = FKT_oB_n \ left (\ frac {S_o} {N_o} \ right) _ {min} $$
Замените вышеуказанное $ S_ {min} $ в следующей стандартной форме уравнения радиолокационной дальности.
$$ R_ {Max} = \ left [\ frac {P_tG \ sigma A_e} {\ left (4 \ pi \ right) ^ 2 S_ {min}} \ right] ^ {1/4} $$
$$ \ Rightarrow R_ {Max} = \ left [\ frac {P_tG \ sigma A_e} {\ left (4 \ pi \ right) ^ 2 FKT_oB_n \ left (\ frac {S_o} {N_o} \ right) _ {мин }} \ right] ^ {1/4} $$
Из приведенного выше уравнения можно сделать вывод, что для получения максимальной дальности действия радара следует учитывать следующие условия .