Асимптотический анализ алгоритма относится к определению математического ограничения / формирования его производительности во время выполнения. Используя асимптотический анализ, мы можем очень хорошо заключить наилучший, средний и худший сценарии алгоритма.
Асимптотический анализ связан с входными данными, т. Е. Если нет входных данных для алгоритма, считается, что он работает в постоянное время. Кроме «входных» все остальные факторы считаются постоянными.
Асимптотический анализ относится к вычислению времени выполнения любой операции в математических единицах вычисления. Например, время выполнения одной операции вычисляется как f (n) и может быть для другой операции оно вычисляется как g (n 2 ). Это означает, что время выполнения первой операции будет линейно увеличиваться с увеличением n, а время выполнения второй операции будет увеличиваться экспоненциально при увеличении n . Точно так же время выполнения обеих операций будет почти одинаковым, если n значительно мало.
Обычно время, требуемое алгоритмом, подразделяется на три типа:
-
Лучший вариант — минимальное время, необходимое для выполнения программы.
-
Средний случай — среднее время, необходимое для выполнения программы.
-
В худшем случае — максимальное время, необходимое для выполнения программы.
Лучший вариант — минимальное время, необходимое для выполнения программы.
Средний случай — среднее время, необходимое для выполнения программы.
В худшем случае — максимальное время, необходимое для выполнения программы.
Асимптотические обозначения
Ниже приведены часто используемые асимптотические обозначения для вычисления сложности алгоритма во время выполнения.
- Ο Обозначение
- Обозначение
- θ нотация
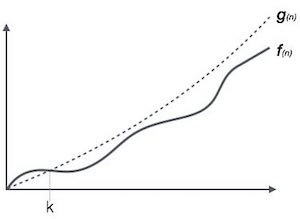
Большая О Нотация, Ο
Обозначение Ο (n) является формальным способом выражения верхней границы времени выполнения алгоритма. Он измеряет сложность времени наихудшего случая или наибольшее время, которое алгоритм может занять для завершения.
Например, для функции f (n)
Ο( f (n)) = { g (n) : there exists c > 0 and n 0 such that f (n) ≤ c. g (n) for all n > n 0 . }
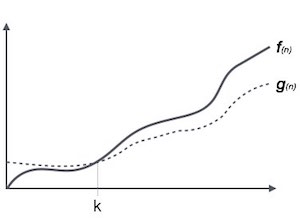
Нотация Омега, Ом
Обозначение Ω (n) является формальным способом выражения нижней границы времени работы алгоритма. Он измеряет наилучшую временную сложность или лучшее время, которое алгоритм может занять для завершения.
Например, для функции f (n)
Ω( f (n)) ≥ { g (n) : there exists c > 0 and n 0 such that g (n) ≤ c. f (n) for all n > n 0 . }
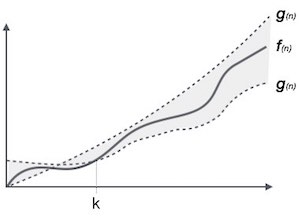
Тета-нотация, θ
Обозначение θ (n) является формальным способом выражения как нижней, так и верхней границы времени выполнения алгоритма. Это представляется следующим образом —
θ( f (n)) = { g (n) if and only if g (n) = Ο( f (n)) and g (n) = Ω( f (n)) for all n > n 0 . }
Распространенные асимптотические обозначения
Ниже приведен список некоторых распространенных асимптотических обозначений —