Структура данных — двоичное дерево поиска

Двоичное дерево поиска (BST) — это дерево, в котором все узлы следуют указанным ниже свойствам:

• Левое поддерево узла имеет ключ, меньший или равный ключу его родительского узла.

• Правое поддерево узла имеет ключ больше, чем ключ его родительского узла.

Левое поддерево узла имеет ключ, меньший или равный ключу его родительского узла.

Правое поддерево узла имеет ключ больше, чем ключ его родительского узла.

Таким образом, BST делит все свои поддеревья на два сегмента; левое поддерево и правое поддерево и может быть определено как —

left_subtree (keys)  ≤  node (key)  ≤  right_subtree (keys)

Представление

BST — это набор узлов, расположенных таким образом, что они поддерживают свойства BST. Каждый узел имеет ключ и соответствующее значение. При поиске нужный ключ сравнивается с ключами в BST, и, если он найден, извлекается соответствующее значение.

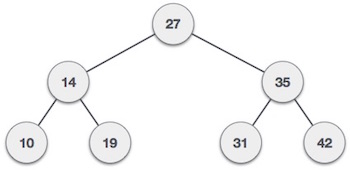
Ниже приведено графическое представление BST —

Мы видим, что ключ корневого узла (27) имеет все менее значимые ключи в левом поддереве и более значимые ключи в правом поддереве.

Основные операции

Ниже приведены основные операции дерева —

• Поиск — поиск элемента в дереве.

• Вставить — вставляет элемент в дерево.

• Предзаказ обхода — обход дерева по предзаказу.

• Порядок обхода — обход дерева по порядку.

• Post-order Traversal — обход дерева по порядку.

Поиск — поиск элемента в дереве.

Вставить — вставляет элемент в дерево.

Предзаказ обхода — обход дерева по предзаказу.

Порядок обхода — обход дерева по порядку.

Post-order Traversal — обход дерева по порядку.

Узел

Определите узел, имеющий некоторые данные, ссылки на его левый и правый дочерние узлы.

struct node {
   int data;   
   struct node *leftChild;
   struct node *rightChild;
};

Операция поиска

Всякий раз, когда необходимо выполнить поиск элемента, начинайте поиск с корневого узла. Затем, если данные меньше значения ключа, найдите элемент в левом поддереве. В противном случае ищите элемент в правом поддереве. Следуйте тому же алгоритму для каждого узла.

Алгоритм

struct node* search(int data){
   struct node *current = root;
   printf("Visiting elements: ");
	
   while(current->data != data){
	
      if(current != NULL) {
         printf("%d ",current->data);
			
         //go to left tree
         if(current->data > data){
            current = current->leftChild;
         }  //else go to right tree
         else {                
            current = current->rightChild;
         }
			
         //not found
         if(current == NULL){
            return NULL;
         }
      }			
   }
   
   return current;
}

Операция вставки

Всякий раз, когда элемент должен быть вставлен, сначала найдите его правильное местоположение. Начните поиск с корневого узла, затем, если данные меньше значения ключа, найдите пустое место в левом поддереве и вставьте данные. В противном случае найдите пустое место в правом поддереве и вставьте данные.