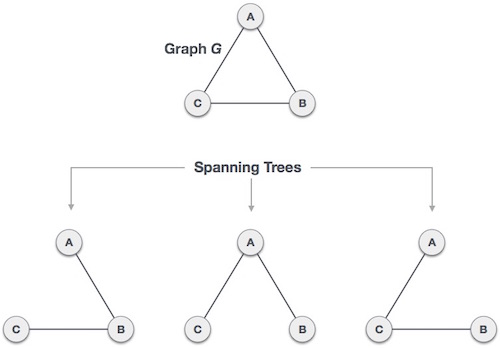
Покрывающее дерево — это подмножество графа G, в котором все вершины покрыты минимально возможным числом ребер. Следовательно, связующее дерево не имеет циклов и не может быть отключено.
По этому определению можно сделать вывод, что у каждого связного и ненаправленного графа G есть хотя бы одно остовное дерево. Несвязанный граф не имеет никакого остовного дерева, так как он не может быть разбит на все его вершины.
Мы нашли три остовных дерева на одном полном графе. Полный неориентированный граф может иметь максимальное количество n -2 связующих деревьев, где n — количество узлов. В приведенном выше примере n равно 3, поэтому возможны 3 3-2 = 3 остовных дерева.
Общие свойства связующего дерева
Теперь мы понимаем, что один граф может иметь более одного связующего дерева. Ниже приведены несколько свойств связующего дерева, связанного с графом G:
-
Связный граф G может иметь более одного связующего дерева.
-
Все возможные остовные деревья графа G имеют одинаковое количество ребер и вершин.
-
В связующем дереве нет циклов (циклов).
-
Удаление одного ребра из связующего дерева приведет к отключению графа, то есть связующее дерево будет минимально связным .
-
Добавление одного ребра в связующее дерево создаст схему или петлю, то есть связующее дерево будет максимально ациклическим .
Связный граф G может иметь более одного связующего дерева.
Все возможные остовные деревья графа G имеют одинаковое количество ребер и вершин.
В связующем дереве нет циклов (циклов).
Удаление одного ребра из связующего дерева приведет к отключению графа, то есть связующее дерево будет минимально связным .
Добавление одного ребра в связующее дерево создаст схему или петлю, то есть связующее дерево будет максимально ациклическим .
Математические свойства связующего дерева
-
Остовное дерево имеет n-1 ребер, где n — количество узлов (вершин).
-
Из полного графа, удалив максимум e — n + 1 ребер, мы можем построить остовное дерево.
-
Полный граф может иметь максимальное количество n-2 связующих деревьев.
Остовное дерево имеет n-1 ребер, где n — количество узлов (вершин).
Из полного графа, удалив максимум e — n + 1 ребер, мы можем построить остовное дерево.
Полный граф может иметь максимальное количество n-2 связующих деревьев.
Таким образом, можно сделать вывод, что остовные деревья являются подмножеством связного графа G, а несвязные графы не имеют остовного дерева.
Применение связующего дерева
Связующее дерево в основном используется, чтобы найти минимальный путь для соединения всех узлов в графе. Обычное применение связующих деревьев —
-
Планирование гражданской сети
-
Протокол маршрутизации компьютерной сети
-
Кластерный анализ
Планирование гражданской сети
Протокол маршрутизации компьютерной сети
Кластерный анализ
Позвольте нам понять это на небольшом примере. Рассмотрим городскую сеть как огромный график и теперь планируем развернуть телефонные линии таким образом, чтобы в минимальных линиях мы могли подключаться ко всем городским узлам. Это где связующее дерево входит в картину.
Минимальное связующее дерево (MST)
В взвешенном графе минимальное остовное дерево — это остовное дерево, которое имеет минимальный вес, чем все остальные остовные деревья того же графа. В реальных ситуациях этот вес может быть измерен как расстояние, затор, транспортная нагрузка или любое произвольное значение, обозначенное по краям.
Минимальный алгоритм связующего дерева
Мы узнаем о двух наиболее важных алгоритмах связующего дерева здесь —
Оба являются жадными алгоритмами.