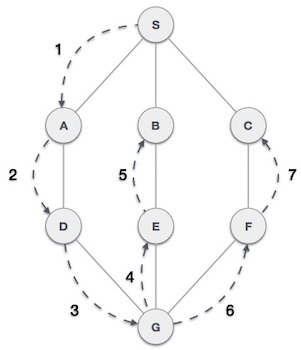
Алгоритм поиска в глубину (DFS) пересекает график при движении вглубь и использует стек для запоминания, чтобы получить следующую вершину для начала поиска, когда тупик возникает на любой итерации.
Как и в приведенном выше примере, алгоритм DFS переходит сначала от S к A, от D к G, от E к B, затем к F и, наконец, к C. В нем применяются следующие правила.
-
Правило 1 — Посетите соседнюю не посещенную вершину. Отметить как посещенный Покажите это. Толкните его в стопку.
-
Правило 2 — Если соседняя вершина не найдена, вытащите вершину из стека. (Появятся все вершины из стека, у которых нет смежных вершин.)
-
Правило 3 — Повторяйте Правило 1 и Правило 2, пока стек не опустеет.
Правило 1 — Посетите соседнюю не посещенную вершину. Отметить как посещенный Покажите это. Толкните его в стопку.
Правило 2 — Если соседняя вершина не найдена, вытащите вершину из стека. (Появятся все вершины из стека, у которых нет смежных вершин.)
Правило 3 — Повторяйте Правило 1 и Правило 2, пока стек не опустеет.
| шаг | пересечение | Описание |
|---|---|---|
| 1 | 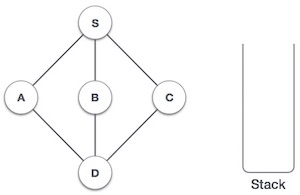 |
Инициализировать стек. |
| 2 | 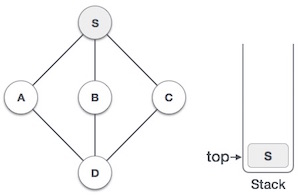 |
Отметьте S как посещенный и поместите его в стек. Исследуйте любой не посещенный соседний узел из S. У нас есть три узла, и мы можем выбрать любой из них. Для этого примера мы возьмем узел в алфавитном порядке. |
| 3 | 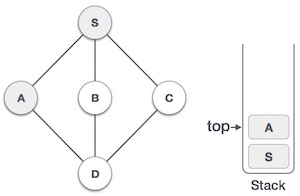 |
Отметьте A как посещенный и поместите его в стек. Исследуйте любой не посещенный соседний узел из A. И S, и D смежны с A, но нас интересуют только не посещенные узлы. |
| 4 | 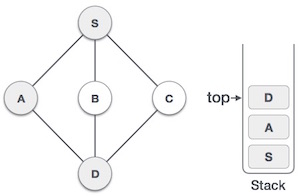 |
Посетите D и отметьте его как посещенный и положите в стек. Здесь у нас есть узлы B и C , которые соседствуют с D и оба не посещаются. Однако мы снова будем выбирать в алфавитном порядке. |
| 5 | 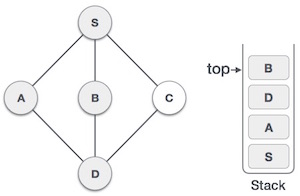 |
Мы выбираем B , отмечаем его как посещенный и помещаем в стек. Здесь B не имеет ни одного не посещенного соседнего узла. Итак, мы выталкиваем B из стека. |
| 6 | 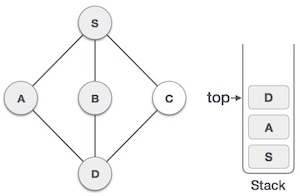 |
Мы проверяем вершину стека на предмет возврата к предыдущему узлу и проверяем, есть ли у него какие-либо не посещенные узлы Здесь мы находим D на вершине стека. |
| 7 | 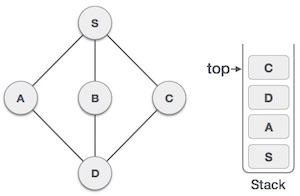 |
Единственный не посещенный соседний узел от D теперь C. Поэтому мы посещаем C , помечаем его как посещенный и помещаем в стек. |
Поскольку C не имеет ни одного не посещенного смежного узла, мы продолжаем выталкивать стек до тех пор, пока не найдем узел, который имеет не посещенный соседний узел. В этом случае их нет, и мы продолжаем появляться, пока стек не опустеет.
Чтобы узнать о реализации этого алгоритма на языке программирования C, нажмите здесь .