Структура данных и алгоритмы - деревья AVL

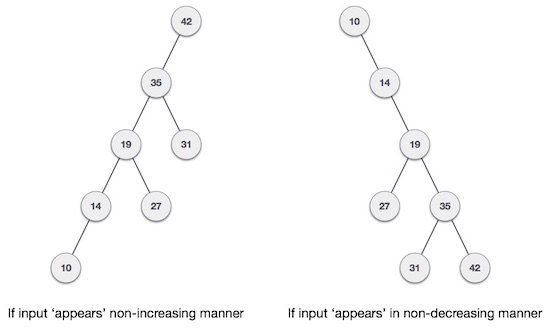
Что если вход в двоичное дерево поиска поступает отсортированным (по возрастанию или по убыванию) образом? Тогда это будет выглядеть так —

Замечено, что производительность BST в худшем случае наиболее близка к алгоритмам линейного поиска, то есть Ο (n). В данных в реальном времени мы не можем предсказать структуру данных и их частоту. Таким образом, возникает необходимость сбалансировать существующий BST.

Названные в честь их изобретателя Adelson , Velski & Landis , деревья AVL представляют собой бинарное дерево поиска с балансировкой высоты. Дерево AVL проверяет высоту левого и правого поддеревьев и гарантирует, что разница не превышает 1. Эта разница называется коэффициентом баланса .

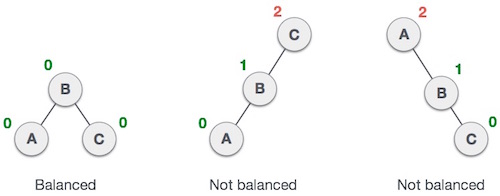
Здесь мы видим, что первое дерево сбалансировано, а следующие два дерева не сбалансированы —

Во втором дереве левое поддерево C имеет высоту 2, а правое поддерево имеет высоту 0, поэтому разница составляет 2. В третьем дереве правое поддерево A имеет высоту 2, а левое отсутствует, поэтому оно равно 0 и снова разница 2. Дерево AVL допускает разницу (коэффициент баланса) только в 1.

BalanceFactor = height(left-sutree) − height(right-sutree)

Если разница в высоте левого и правого поддеревьев превышает 1, дерево уравновешивается с использованием некоторых методов поворота.

AVL Rotations

Чтобы сбалансировать себя, дерево AVL может выполнять следующие четыре вида вращений:

Левый поворот
Правое вращение
Вращение влево-вправо
Вращение вправо-влево

Первые два вращения — это одиночные вращения, а следующие два вращения — двойные вращения. Чтобы иметь несбалансированное дерево, нам нужно, по крайней мере, дерево высоты 2. С этим простым деревом, давайте разберемся с ними один за другим.

Левый поворот

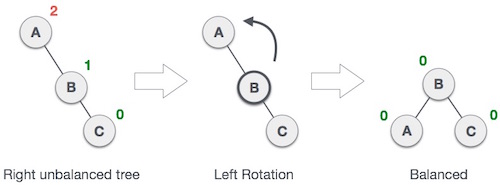
Если дерево становится неуравновешенным, когда узел вставляется в правое поддерево правого поддерева, мы выполняем одиночное вращение влево —

В нашем примере узел A стал неуравновешенным, поскольку узел вставлен в правое поддерево правого поддерева A. Мы выполняем вращение влево, делая A левым поддеревом B.

Правое вращение

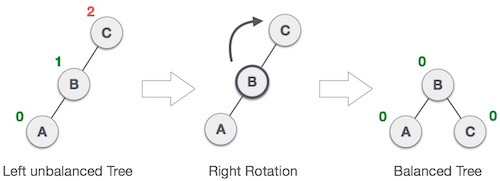
Дерево AVL может стать несбалансированным, если узел вставлен в левое поддерево левого поддерева. Дерево тогда нуждается в правильном вращении.

Как изображено, несбалансированный узел становится правым потомком своего левого потомка, выполняя правое вращение.

Вращение вправо-влево

Двойные повороты — немного сложная версия уже объясненных версий поворотов. Чтобы понять их лучше, мы должны принять к сведению каждое действие, выполненное во время вращения. Давайте сначала проверим, как выполнить вращение влево-вправо. Поворот влево-вправо — это комбинация вращения влево, за которым следует поворот вправо.

государственный	действие
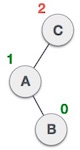	Узел был вставлен в правое поддерево левого поддерева. Это делает C несбалансированным узлом. Эти сценарии заставляют дерево AVL выполнять вращение влево-вправо.
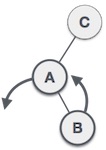	Сначала мы выполняем левый поворот на левом поддереве C. Это делает A , левое поддерево B.
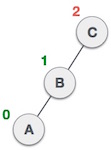	Узел C все еще не сбалансирован, однако теперь это происходит из-за левого поддерева левого поддерева.
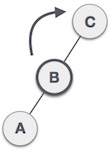	Теперь мы повернем дерево вправо, сделав B новым корневым узлом этого поддерева. C теперь становится правым поддеревом своего собственного левого поддерева.
	Дерево теперь сбалансировано.