Структура данных и алгоритмы — Дерево

Дерево представляет собой узлы, соединенные ребрами. Мы обсудим двоичное дерево или двоичное дерево поиска конкретно.

Двоичное дерево — это специальная структура данных, используемая для хранения данных. Бинарное дерево имеет специальное условие, что каждый узел может иметь максимум двух дочерних элементов. Двоичное дерево имеет преимущества как упорядоченного массива, так и связанного списка, поскольку поиск выполняется так же быстро, как в отсортированном массиве, а операции вставки или удаления выполняются так же быстро, как и в связанном списке.

Важные условия

Ниже приведены важные термины относительно дерева.

• Путь — путь относится к последовательности узлов по краям дерева.

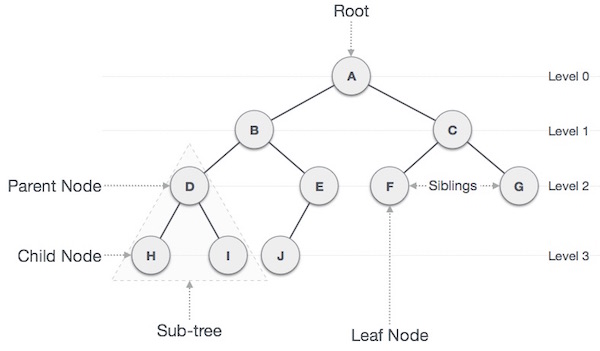
• Корень — узел в верхней части дерева называется корнем. Существует только один корень на дерево и один путь от корневого узла к любому узлу.

• Родитель — Любой узел, кроме корневого, имеет один край вверх к узлу, называемому родительским.

• Дочерний — узел ниже заданного узла, соединенного его ребром вниз, называется его дочерним узлом.

• Лист — узел, у которого нет дочернего узла, называется листовым узлом.

• Поддерево — Поддерево представляет потомков узла.

• Посещение — Посещение относится к проверке значения узла, когда управление находится на узле.

• Обход — Обход означает прохождение через узлы в определенном порядке.

• Уровни — Уровень узла представляет генерацию узла. Если корневой узел находится на уровне 0, то его следующий дочерний узел находится на уровне 1, его внук — на уровне 2 и т. Д.

• keys — Key представляет значение узла, на основе которого должна выполняться операция поиска для узла.

Путь — путь относится к последовательности узлов по краям дерева.

Корень — узел в верхней части дерева называется корнем. Существует только один корень на дерево и один путь от корневого узла к любому узлу.

Родитель — Любой узел, кроме корневого, имеет один край вверх к узлу, называемому родительским.

Дочерний — узел ниже заданного узла, соединенного его ребром вниз, называется его дочерним узлом.

Лист — узел, у которого нет дочернего узла, называется листовым узлом.

Поддерево — Поддерево представляет потомков узла.

Посещение — Посещение относится к проверке значения узла, когда управление находится на узле.

Обход — Обход означает прохождение через узлы в определенном порядке.

Уровни — Уровень узла представляет генерацию узла. Если корневой узел находится на уровне 0, то его следующий дочерний узел находится на уровне 1, его внук — на уровне 2 и т. Д.

keys — Key представляет значение узла, на основе которого должна выполняться операция поиска для узла.

Представление дерева двоичного поиска

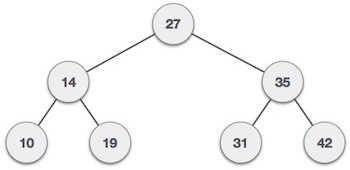
Дерево бинарного поиска обладает особым поведением. Левый потомок узла должен иметь значение меньше значения его родителя, а правый потомок узла должен иметь значение больше, чем значение его родителя.

Мы собираемся реализовать дерево, используя объект узла и соединяя их через ссылки.

Узел дерева

Код для написания узла дерева будет похож на приведенный ниже. Он имеет часть данных и ссылки на его левый и правый дочерние узлы.

struct node {
   int data;   
   struct node *leftChild;
   struct node *rightChild;
};

В дереве все узлы имеют общую конструкцию.

BST Основные операции

Основные операции, которые могут быть выполнены над структурой данных бинарного дерева поиска, следующие:

• Вставить — вставляет элемент в дерево / создает дерево.

• Поиск — поиск элемента в дереве.

• Preorder Traversal — обход дерева по предзаказу.

• Inorder Traversal — обход дерева по порядку.

• Postorder Traversal — обход дерева по порядку заказа.

Вставить — вставляет элемент в дерево / создает дерево.

Поиск — поиск элемента в дереве.

Preorder Traversal — обход дерева по предзаказу.

Inorder Traversal — обход дерева по порядку.

Postorder Traversal — обход дерева по порядку заказа.

Мы научимся создавать (вставлять в) древовидную структуру и искать элемент данных в дереве в этой главе. Мы узнаем о методах обхода дерева в следующей главе.

Операция вставки

Самая первая вставка создает дерево. После этого всякий раз, когда необходимо вставить элемент, сначала найдите его правильное местоположение. Начните поиск с корневого узла, затем, если данные меньше значения ключа, найдите пустое место в левом поддереве и вставьте данные. В противном случае найдите пустое место в правом поддереве и вставьте данные.

Алгоритм

If root is NULL 
   then create root node
return

If root exists then
   compare the data with node.data
   
   while until insertion position is located

      If data is greater than node.data
         goto right subtree
      else
         goto left subtree

   endwhile 
   
   insert data
	
end If      

Реализация

Реализация функции вставки должна выглядеть так:

void insert(int data) {
   struct node *tempNode = (struct node*) malloc(sizeof(struct node));
   struct node *current;
   struct node *parent;

   tempNode->data = data;
   tempNode->leftChild = NULL;
   tempNode->rightChild = NULL;

   //if tree is empty, create root node
   if(root == NULL) {
      root = tempNode;
   } else {
      current = root;
      parent  = NULL;

      while(1) {                
         parent = current;

         //go to left of the tree
         if(data < parent->data) {
            current = current->leftChild;                
            
            //insert to the left
            if(current == NULL) {
               parent->leftChild = tempNode;
               return;
            }
         }
			
         //go to right of the tree
         else {
            current = current->rightChild;
            
            //insert to the right
            if(current == NULL) {
               parent->rightChild = tempNode;
               return;
            }
         }
      }            
   }
}

Операция поиска

Всякий раз, когда необходимо выполнить поиск элемента, начинайте поиск с корневого узла, затем, если данные меньше значения ключа, ищите элемент в левом поддереве. В противном случае ищите элемент в правом поддереве. Следуйте тому же алгоритму для каждого узла.

Алгоритм

If root.data is equal to search.data
   return root
else
   while data not found

      If data is greater than node.data
         goto right subtree
      else
         goto left subtree
         
      If data found
         return node
   endwhile 
   
   return data not found
   
end if      

Реализация этого алгоритма должна выглядеть следующим образом.

struct node* search(int data) {
   struct node *current = root;
   printf("Visiting elements: ");

   while(current->data != data) {
      if(current != NULL)
      printf("%d ",current->data); 
      
      //go to left tree

      if(current->data > data) {
         current = current->leftChild;
      }
      //else go to right tree
      else {                
         current = current->rightChild;
      }

      //not found
      if(current == NULL) {
         return NULL;
      }

      return current;
   }  
}

Чтобы узнать о реализации структуры данных бинарного дерева поиска, нажмите здесь .