Граф представляет собой графическое представление набора объектов, где некоторые пары объектов связаны ссылками. Взаимосвязанные объекты представлены точками, называемыми вершинами , а связи, соединяющие вершины, называются ребрами .
Формально граф представляет собой пару множеств (V, E) , где V — множество вершин, а E — множество ребер, соединяющих пары вершин. Посмотрите на следующий график —
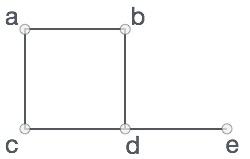
На приведенном выше графике
V = {a, b, c, d, e}
E = {ab, ac, bd, cd, de}
Структура данных графика
Математические графики могут быть представлены в структуре данных. Мы можем представить граф, используя массив вершин и двумерный массив ребер. Прежде чем мы продолжим, давайте ознакомимся с некоторыми важными терминами —
-
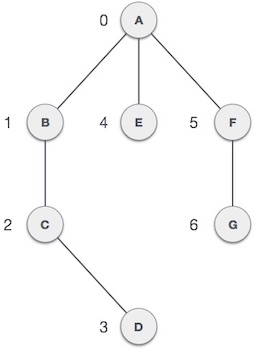
Вершина — каждый узел графа представлен как вершина. В следующем примере помеченный кружок представляет вершины. Таким образом, от A до G являются вершинами. Мы можем представить их, используя массив, как показано на следующем рисунке. Здесь A можно идентифицировать по индексу 0. B можно идентифицировать по индексу 1 и так далее.
-
Край — Край представляет собой путь между двумя вершинами или линию между двумя вершинами. В следующем примере линии от A до B, B до C и т. Д. Представляют ребра. Мы можем использовать двумерный массив для представления массива, как показано на следующем рисунке. Здесь AB можно представить как 1 в строке 0, столбце 1, BC как 1 в строке 1, столбце 2 и т. Д., Оставив другие комбинации равными 0.
-
Смежность — два узла или вершины являются смежными, если они соединены друг с другом через ребро. В следующем примере B смежен с A, C смежен с B и так далее.
-
Путь — Путь представляет собой последовательность ребер между двумя вершинами. В следующем примере ABCD представляет путь от A до D.
Вершина — каждый узел графа представлен как вершина. В следующем примере помеченный кружок представляет вершины. Таким образом, от A до G являются вершинами. Мы можем представить их, используя массив, как показано на следующем рисунке. Здесь A можно идентифицировать по индексу 0. B можно идентифицировать по индексу 1 и так далее.
Край — Край представляет собой путь между двумя вершинами или линию между двумя вершинами. В следующем примере линии от A до B, B до C и т. Д. Представляют ребра. Мы можем использовать двумерный массив для представления массива, как показано на следующем рисунке. Здесь AB можно представить как 1 в строке 0, столбце 1, BC как 1 в строке 1, столбце 2 и т. Д., Оставив другие комбинации равными 0.
Смежность — два узла или вершины являются смежными, если они соединены друг с другом через ребро. В следующем примере B смежен с A, C смежен с B и так далее.
Путь — Путь представляет собой последовательность ребер между двумя вершинами. В следующем примере ABCD представляет путь от A до D.
Основные операции
Ниже приведены основные основные операции графа —
-
Добавить вершину — добавляет вершину на график.
-
Добавить ребро — добавляет ребро между двумя вершинами графа.
-
Отображать вершину — отображает вершину графика.
Добавить вершину — добавляет вершину на график.
Добавить ребро — добавляет ребро между двумя вершинами графа.
Отображать вершину — отображает вершину графика.
Чтобы узнать больше о графике, пожалуйста, прочитайте учебник теории графов . Мы узнаем о прохождении графа в следующих главах.