Структура данных и алгоритмы — Ханойская башня

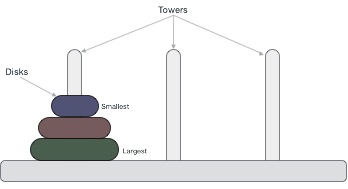
Ханойская башня, это математическая головоломка, которая состоит из трех башен (колышков) и более одного кольца, как изображено —

Эти кольца имеют разные размеры и сложены в порядке возрастания, то есть меньшее помещается над большим. Существуют и другие варианты головоломки, в которых количество дисков увеличивается, но количество башен остается неизменным.

правила

Миссия состоит в том, чтобы переместить все диски в какую-то другую башню, не нарушая последовательность расположения. Вот несколько правил, которым нужно следовать для Ханойской башни:

• Только один диск может быть перемещен среди башен в любой момент времени.
• Только «верхний» диск может быть удален.
• Ни один большой диск не может сидеть над маленьким диском.

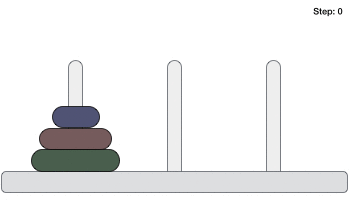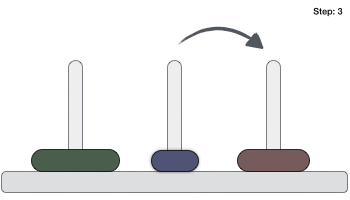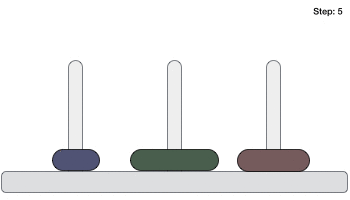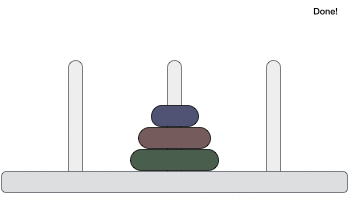
Ниже приводится анимационное изображение решения головоломки Ханойской башни с тремя дисками.

Загадка Ханойской башни с n дисками может быть решена минимум за 2 ⁿ −1 шагов. Эта презентация показывает, что головоломка с 3 дисками прошла 2 ³ — 1 = 7 шагов.

Алгоритм

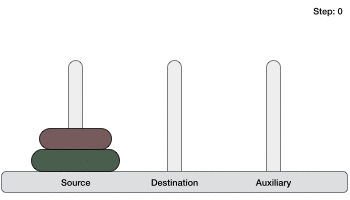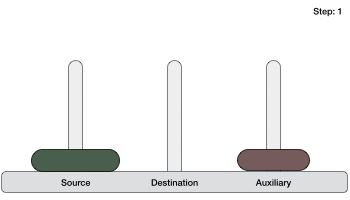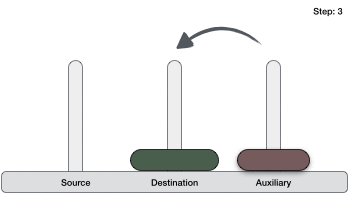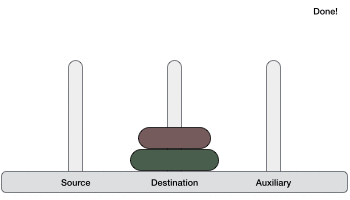
Чтобы написать алгоритм для Ханойской башни, сначала нам нужно научиться решать эту проблему с меньшим количеством дисков, скажем, → 1 или 2. Мы помечаем три башни с именем, источником , местом назначения и вспомогательным (только для перемещения дисков. ). Если у нас есть только один диск, он может быть легко перемещен из исходной точки в точку привязки.

Если у нас есть 2 диска —

• Во-первых, мы перемещаем меньший (верхний) диск в aug peg.
• Затем мы перемещаем больший (нижний) диск в целевой колышек.
• И, наконец, мы перемещаем меньший диск из вспомогательной в конечную привязку.

Итак, теперь мы можем разработать алгоритм для Ханойской башни с более чем двумя дисками. Разобьем стек дисков на две части. Самый большой диск (n- ^й диск) находится в одной части, а все остальные (n-1) — во второй части.

Наша конечная цель — переместить диск n из источника в место назначения, а затем поместить на него все остальные (n1) диски. Мы можем представить, чтобы применить это же рекурсивное решение для всего данного набора дисков.

Следующие шаги —

Step 1 − Move n-1 disks from source to aux
Step 2 − Move n th disk from source to dest
Step 3 − Move n-1 disks from aux to dest

Рекурсивный алгоритм для Ханойской башни может быть реализован следующим образом:

START
Procedure Hanoi(disk, source, dest, aux)

   IF disk == 1, THEN
      move disk from source to dest             
   ELSE
      Hanoi(disk - 1, source, aux, dest)     // Step 1
      move disk from source to dest          // Step 2
      Hanoi(disk - 1, aux, dest, source)     // Step 3
   END IF
   
END Procedure
STOP

Чтобы проверить реализацию в C-программировании, нажмите здесь .