Основное использование отсечения в компьютерной графике — удаление объектов, линий или отрезков, которые находятся за пределами области просмотра. Преобразование просмотра нечувствительно к положению точек относительно объема просмотра — особенно тех точек, которые находятся за зрителем — и необходимо удалить эти точки перед созданием вида.
Точка отсечения
Вырезать точку из заданного окна очень легко. Рассмотрим следующий рисунок, где прямоугольник указывает окно. Отсечение точек говорит нам, находится ли данная точка (X, Y) в данном окне или нет; и решает, будем ли мы использовать минимальные и максимальные координаты окна.
Координата X данной точки находится внутри окна, если X лежит между Wx1 ≤ X ≤ Wx2. Точно так же, координата Y данной точки находится внутри окна, если Y лежит между Wy1 ≤ Y ≤ Wy2.
Обрезка линии
Концепция отсечения линий такая же, как и отсечение точек. При вырезании строки мы обрежем часть строки, которая находится за пределами окна, и оставим только часть, которая находится внутри окна.
Отрезки Коэн-Сазерлендской Линии
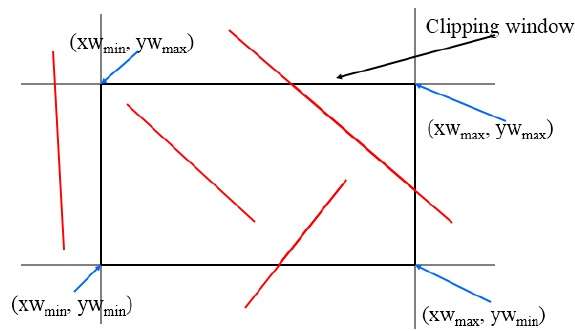
Этот алгоритм использует окно отсечения, как показано на следующем рисунке. Минимальная координата для области отсечения составляет $ (XW_ {min,} YW_ {min}) $, а максимальная координата для области отсечения составляет $ (XW_ {max,} YW_ {max}) $.
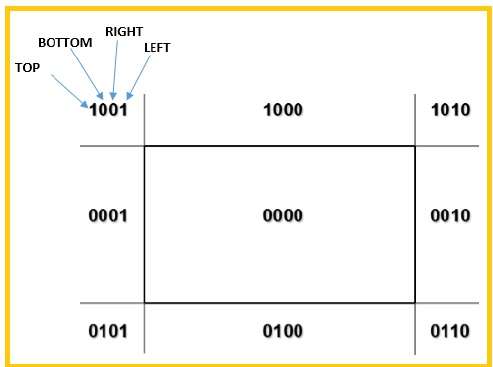
Мы будем использовать 4 бита, чтобы разделить весь регион. Эти 4 бита представляют верхнюю, нижнюю, правую и левую части области, как показано на следующем рисунке. Здесь биты TOP и LEFT установлены в 1, потому что это угол TOP-LEFT .
Есть 3 возможности для линии —
-
Линия может быть полностью внутри окна (эта строка должна быть принята).
-
Линия может быть полностью за пределами окна (эта линия будет полностью удалена из региона).
-
Линия может быть частично внутри окна (мы найдем точку пересечения и нарисуем только ту часть линии, которая находится внутри области).
Линия может быть полностью внутри окна (эта строка должна быть принята).
Линия может быть полностью за пределами окна (эта линия будет полностью удалена из региона).
Линия может быть частично внутри окна (мы найдем точку пересечения и нарисуем только ту часть линии, которая находится внутри области).
Алгоритм
Шаг 1 — Назначьте код региона для каждой конечной точки.
Шаг 2 — Если обе конечные точки имеют код региона 0000, тогда примите эту строку.
Шаг 3 — В противном случае выполните логическую операцию И для обоих кодов региона.
Шаг 3.1 — Если результат не 0000, отклоните строку.
Шаг 3.2 — иначе вам нужно отсечь.
Шаг 3.2.1 — Выберите конечную точку линии, которая находится за пределами окна.
Шаг 3.2.2 — Найти точку пересечения на границе окна (на основе кода региона).
Шаг 3.2.3 — Заменить конечную точку точкой пересечения и обновить код региона.
Шаг 3.2.4 — Повторяйте шаг 2, пока мы не найдем обрезанную линию, либо тривиально принятую, либо тривиально отклоненную.
Шаг 4 — Повторите шаг 1 для других строк.
Cyrus-Beck Алгоритм отсечения строки
Этот алгоритм более эффективен, чем алгоритм Коэна-Сазерленда. Он использует параметрическое линейное представление и простые точечные произведения.
Параметрическое уравнение прямой —
P 0 P 1 :P(t) = P 0 + t(P 1 - P 0 )
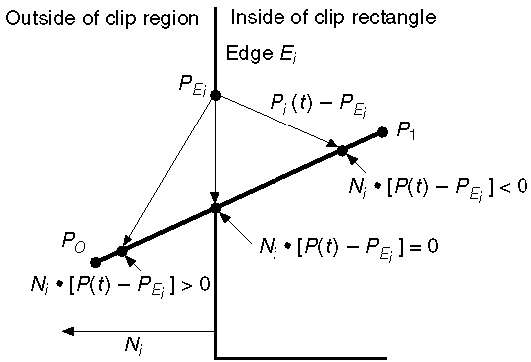
Пусть N i — внешнее нормальное ребро E i . Теперь выберите любую произвольную точку P Ei на ребре E i, тогда произведение точек N i . [P (t) — P Ei ] определяет, находится ли точка P (t) «внутри края клипа» или «вне» края клипа или «На» край клипа.
Точка P (t) находится внутри, если N i . [P (t) — P Ei ] <0
Точка P (t) находится снаружи, если N i . [P (t) — P Ei ]> 0
Точка P (t) находится на краю, если N i . [P (t) — P Ei ] = 0 (точка пересечения)
N i . [P (t) — P Ei ] = 0
N i . [P 0 + t (P 1 — P 0 ) — P Ei ] = 0 (замена P (t) на P 0 + t (P 1 — P 0 ))
N i . [P 0 — P Ei ] + N i .t [P 1 — P 0 ] = 0
N i . [P 0 — P Ei ] + N i ∙ tD = 0 (заменяя D на [P 1 — P 0 ])
N i . [P 0 — P Ei ] = — N i ∙ tD
Уравнение для т становится,
$$ t = \ tfrac {N_ {i}. [P_ {o} — P_ {Ei}]} {{- N_ {i} .D}} $$
Это действительно для следующих условий —
- N i ≠ 0 (ошибка не может произойти)
- D ≠ 0 (P 1 ≠ P 0 )
- N i ∙ D ≠ 0 (P 0 P 1 не параллельно E i )
Обрезка полигонов (алгоритм Сазерленда Ходжмана)
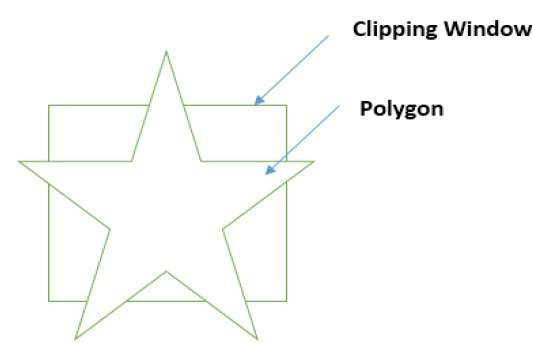
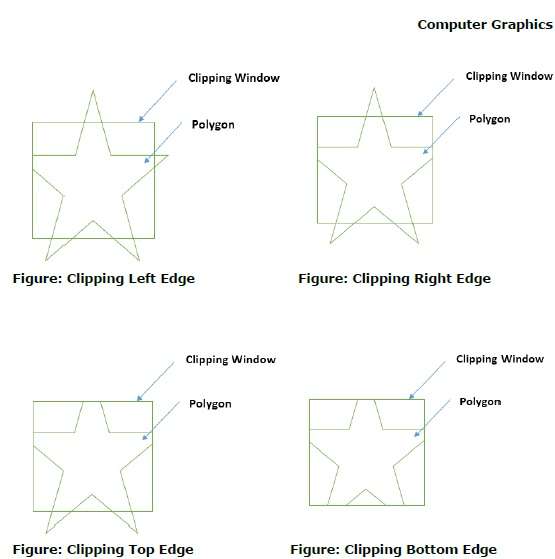
Многоугольник также можно вырезать, указав окно отсечения. Алгоритм отсечения полигонов Сазерленда Ходжмана используется для отсечения полигонов. В этом алгоритме все вершины многоугольника обрезаются у каждого края окна отсечения.
Сначала полигон обрезается по левому краю окна многоугольника, чтобы получить новые вершины многоугольника. Эти новые вершины используются для обрезки многоугольника по правому краю, верхнему краю, нижнему краю окна отсечения, как показано на следующем рисунке.
При обработке края многоугольника с окном отсечения точка пересечения находится, если край не полностью находится внутри окна отсечения, а частичный край от точки пересечения к внешнему краю отсечен. На следующих рисунках показаны вырезки слева, справа, сверху и снизу —
Обрезка текста
Различные методы используются для обеспечения отсечения текста в компьютерной графике. Это зависит от методов, используемых для генерации символов, и требований конкретного приложения. Есть три метода для обрезки текста, которые перечислены ниже —
- Отсечение строк полностью или без
- Обрезка всех или ни одного символа
- Вырезка текста
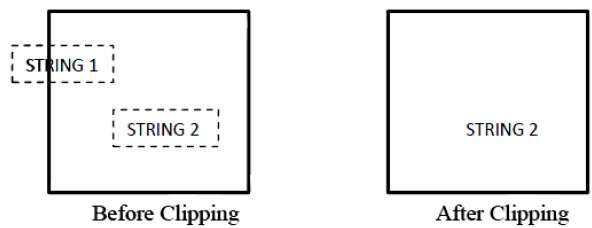
На следующем рисунке показано полное или нулевое отсечение строки —
В методе отсечения строк полностью или ни при каких условиях мы сохраняем всю строку или отклоняем всю строку на основе окна отсечения. Как показано на рисунке выше, STRING2 полностью находится внутри окна отсечения, поэтому мы сохраняем его, а STRING1 лишь частично находится внутри окна, и мы его отвергаем.
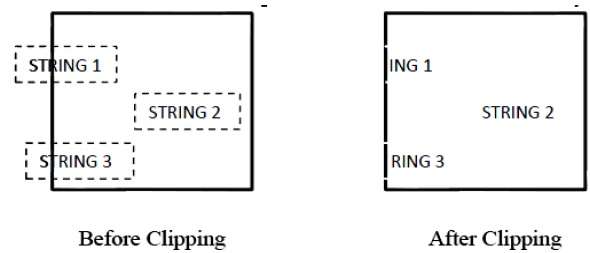
На следующем рисунке показано полное или полное отсутствие символов.
Этот метод отсечения основан на символах, а не на всей строке. В этом методе, если строка полностью находится внутри окна отсечения, мы сохраняем ее. Если это частично за окном, то —
-
Вы отклоняете только ту часть строки, которая находится снаружи
-
Если символ находится на границе окна отсечения, то мы отбрасываем весь этот символ и сохраняем оставшуюся строку.
Вы отклоняете только ту часть строки, которая находится снаружи
Если символ находится на границе окна отсечения, то мы отбрасываем весь этот символ и сохраняем оставшуюся строку.
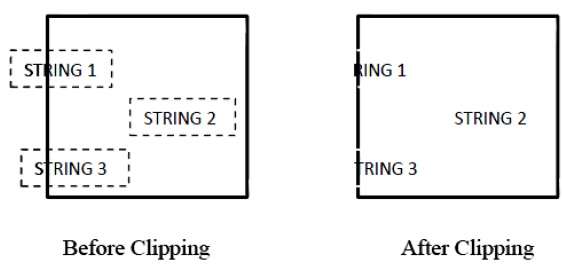
На следующем рисунке показано вырезание текста —
Этот метод отсечения основан на символах, а не на всей строке. В этом методе, если строка полностью находится внутри окна отсечения, мы сохраняем ее. Если это частично за окном, то
-
Вы отклоняете только ту часть строки, которая находится снаружи.
-
Если символ находится на границе окна отсечения, то мы отбрасываем только ту часть символа, которая находится за пределами окна отсечения.
Вы отклоняете только ту часть строки, которая находится снаружи.
Если символ находится на границе окна отсечения, то мы отбрасываем только ту часть символа, которая находится за пределами окна отсечения.
Растровая графика
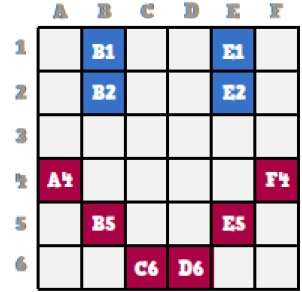
Растровое изображение — это набор пикселей, который описывает изображение. Это тип компьютерной графики, которую компьютер использует для хранения и отображения изображений. В этом типе графики изображения хранятся по крупицам и, следовательно, они называются «Битовая карта». Для лучшего понимания давайте рассмотрим следующий пример, где мы рисуем смайлик с помощью растровой графики.
Теперь мы увидим, как это улыбающееся лицо по крупицам хранится в компьютерной графике.
Внимательно наблюдая за исходным смайликом, мы можем видеть, что есть две синие линии, которые представлены как B1, B2 и E1, E2 на рисунке выше.
Таким же образом смайлик представлен с использованием комбинационных битов A4, B5, C6, D6, E5 и F4 соответственно.
Основными недостатками растровой графики являются —
Мы не можем изменить размер растрового изображения. Если вы попытаетесь изменить размер, пиксели будут размыты.
Цветные растровые изображения могут быть очень большими.