3D трансформация

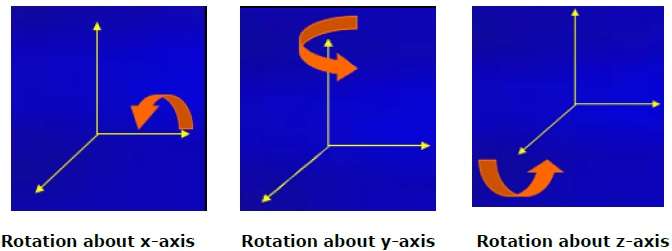
3D-вращение не совпадает с 2D-вращением. В трехмерном вращении мы должны указать угол поворота вместе с осью вращения. Мы можем выполнить трехмерное вращение вокруг осей X, Y и Z. Они представлены в виде матрицы, как показано ниже —

$$R_ {x} (\ theta) = \ begin {bmatrix} 1 & 0 & 0 & 0 \\ 0 & cos \ theta & −sin \ theta & 0 \\ 0 & sin \ theta & cos \ theta & 0 \\ 0 & 0 & 0 & 1 \ \ \ end {bmatrix} R_ {y} (\ theta) = \ begin {bmatrix} cos \ theta & 0 & sin \ theta & 0 \\ 0 & 1 & 0 & 0 \\ −sin \ theta & 0 & cos \ theta & 0 \ cos 0 & 0 & 0 & 1 \\ \ end {bmatrix} R_ {z} (\ theta) = \ begin {bmatrix} cos \ theta & −sin \ theta & 0 & 0 \\ sin \ theta & cos \ theta & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \ end {bmatrix}$$

На следующем рисунке показано вращение вокруг различных осей —

пересчет

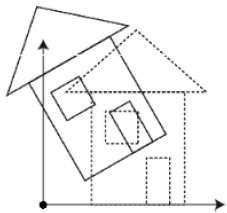
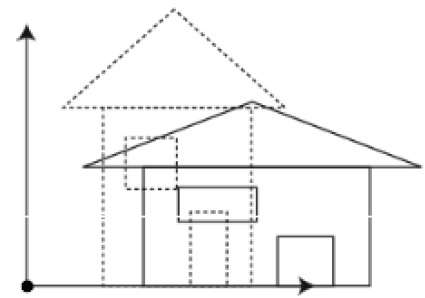
Вы можете изменить размер объекта, используя масштабное преобразование. В процессе масштабирования вы либо расширяете, либо сжимаете размеры объекта. Масштабирование может быть достигнуто путем умножения исходных координат объекта на коэффициент масштабирования, чтобы получить желаемый результат. На следующем рисунке показан эффект 3D-масштабирования —

В операции трехмерного масштабирования используются три координаты. Предположим, что исходные координаты (X, Y, Z), коэффициенты масштабирования равны $(S_ {X,} S_ {Y,} S_ {z})$ соответственно, а полученные координаты — (X ‘, Y’ Z ‘). Это может быть математически представлено, как показано ниже —

$S = \ begin {bmatrix} S_ {x} & 0 & 0 & 0 \\ 0 & S_ {y} & 0 & 0 \\ 0 & 0 & S_ {z} & 0 \\ 0 & 0 & 0 & 1 \ end {bmatrix}$

P ‘= P ∙ S

$[{X} '\: \: \: {Y}' \: \: \: {Z} '\: \: \: 1] = [X \: \: \: Y \: \: \: Z \: \: \: 1] \: \: \ begin {bmatrix} S_ {x} & 0 & 0 & 0 \ 0 & 0 & S_ {y} & 0 & 0 \\ 0 & 0 & S_ {z} & 0 \\ 0 & 0 & 0 & 1 \ end {bmatrix}$

=[X.SxY.SyZ.Sz1]$= [X.S_ {x} \: \: \: Y.S_ {y} \: \: \: Z.S_ {z} \: \: \: 1]$

ножницы

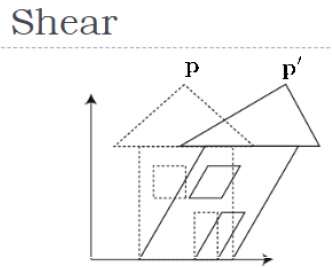
Преобразование, которое наклоняет форму объекта, называется сдвиговым преобразованием . Как и в 2D-сдвиге, мы можем сдвигать объект по оси X, Y или Z в 3D.

Как показано на рисунке выше, есть координата P. Вы можете сдвинуть ее, чтобы получить новую координату P ‘, которую можно представить в виде трехмерной матрицы, как показано ниже:

$Sh = \ begin {bmatrix} 1 & sh_ {x} ^ {y} & sh_ {x} ^ {z} & 0 \\ sh_ {y} ^ {x} & 1 & sh_ {y} ^ {z} & 0 \\ sh_ {z} ^ {x} & sh_ {z} ^ {y} & 1 & 0 \\ 0 & 0 & 0 & 1 \ end {bmatrix}$

P ‘= P ∙ Sh

$X '= X + Sh_ {x} ^ {y} Y + Sh_ {x} ^ {z} Z$

$Y '= Sh_ {y} ^ {x} X + Y + sh_ {y} ^ {z} Z$

$Z '= Sh_ {z} ^ {x} X + Sh_ {z} ^ {y} Y + Z$

Матрицы преобразования

Матрица преобразования является основным инструментом для преобразования. Матрица с размерами nxm умножается на координаты объектов. Обычно для преобразования используются матрицы 3 x 3 или 4 x 4. Например, рассмотрим следующую матрицу для различных операций.