Кривые компьютерной графики

В компьютерной графике нам часто приходится рисовать различные типы объектов на экране. Объекты не всегда плоские, и нам нужно много раз рисовать кривые, чтобы нарисовать объект.

Типы кривых

Кривая — это бесконечно большое множество точек. У каждой точки есть два соседа, кроме конечных. Кривые можно в целом разделить на три категории — явные, неявные и параметрические .

Неявные кривые

Неявные представления кривой определяют набор точек на кривой, используя процедуру, которая может проверить, находится ли точка на кривой. Обычно неявная кривая определяется неявной функцией вида —

f (x, y) = 0

Он может представлять многозначные кривые (несколько значений y для значения x). Типичным примером является круг, неявное представление которого

х ² + у ² — R ² = 0

Явные кривые

Математическая функция y = f (x) может быть построена в виде кривой. Такая функция является явным представлением кривой. Явное представление не является общим, поскольку оно не может представлять вертикальные линии и также является однозначным. Для каждого значения x функция вычисляет только одно значение y.

Параметрические Кривые

Кривые, имеющие параметрическую форму, называются параметрическими кривыми. Явное и неявное представление кривой можно использовать только тогда, когда функция известна. На практике используются параметрические кривые. Двумерная параметрическая кривая имеет следующий вид —

P (t) = f (t), g (t) или P (t) = x (t), y (t)

Функции f и g становятся координатами (x, y) любой точки на кривой, и точки получаются, когда параметр t изменяется в течение определенного интервала [a, b], обычно [0, 1].

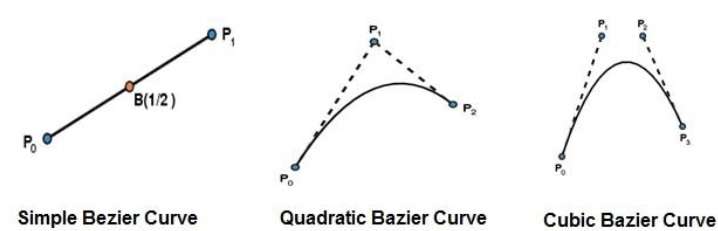
Кривые Безье

Кривая Безье обнаружена французским инженером Пьером Безье . Эти кривые могут быть сгенерированы под контролем других точек. Приблизительные касательные с использованием контрольных точек используются для создания кривой. Кривая Безье может быть представлена ​​математически как —

$$\ sum_ {k = 0} ^ {n} P_ {i} {B_ {i} ^ {n}} (t)$$

Где $p_ {i}$ — множество точек, а ${B_ {i} ^ {n}} (t)$ — полиномы Бернштейна, которые задаются как —

$${B_ {i} ^ {n}} (t) = \ binom {n} {i} (1 - t) ^ {ni} t ^ {i}$$

Где n — степень полинома, i — индекс, а t — переменная.

Самая простая кривая Безье — это прямая линия от точки $P_ {0}$ до $P_ {1}$. Квадратичная кривая Безье определяется тремя контрольными точками. Кубическая кривая Безье определяется четырьмя контрольными точками.

Свойства кривых Безье

Кривые Безье имеют следующие свойства —

• Они обычно следуют форме контрольного многоугольника, который состоит из сегментов, соединяющих контрольные точки.

• Они всегда проходят через первую и последнюю контрольные точки.

• Они содержатся в выпуклой оболочке их определяющих контрольных точек.

• Степень полинома, определяющего сегмент кривой, на единицу меньше числа определяющей точки многоугольника. Следовательно, для 4 контрольных точек степень многочлена равна 3, то есть кубический многочлен.

• Кривая Безье, как правило, повторяет форму определяющего многоугольника.

• Направление касательного вектора в конечных точках совпадает с направлением вектора, определяемого первым и последним сегментами.

• Свойство выпуклой оболочки для кривой Безье гарантирует, что многочлен плавно следует контрольным точкам.

• Ни одна прямая линия не пересекает кривую Безье больше, чем она пересекает ее управляющий многоугольник.

• Они инвариантны при аффинном преобразовании.

• Кривые Безье демонстрируют глобальное управление, то есть перемещение контрольной точки изменяет форму всей кривой.

• Данная кривая Безье может быть подразделена в точке t = t0 на два сегмента Безье, которые объединяются в точке, соответствующей значению параметра t = t0.

Они обычно следуют форме контрольного многоугольника, который состоит из сегментов, соединяющих контрольные точки.

Они всегда проходят через первую и последнюю контрольные точки.

Они содержатся в выпуклой оболочке их определяющих контрольных точек.

Степень полинома, определяющего сегмент кривой, на единицу меньше числа определяющей точки многоугольника. Следовательно, для 4 контрольных точек степень многочлена равна 3, то есть кубический многочлен.

Кривая Безье, как правило, повторяет форму определяющего многоугольника.

Направление касательного вектора в конечных точках совпадает с направлением вектора, определяемого первым и последним сегментами.

Свойство выпуклой оболочки для кривой Безье гарантирует, что многочлен плавно следует контрольным точкам.

Ни одна прямая линия не пересекает кривую Безье больше, чем она пересекает ее управляющий многоугольник.

Они инвариантны при аффинном преобразовании.

Кривые Безье демонстрируют глобальное управление, то есть перемещение контрольной точки изменяет форму всей кривой.

Данная кривая Безье может быть подразделена в точке t = t0 на два сегмента Безье, которые объединяются в точке, соответствующей значению параметра t = t0.

Кривые B-сплайнов

Кривая Безье, полученная базисной функцией Бернштейна, обладает ограниченной гибкостью.

• Во-первых, количество указанных вершин многоугольника фиксирует порядок получающегося полинома, который определяет кривую.

• Вторая ограничивающая характеристика заключается в том, что значение функции смешивания отлично от нуля для всех значений параметров по всей кривой.

Во-первых, количество указанных вершин многоугольника фиксирует порядок получающегося полинома, который определяет кривую.

Вторая ограничивающая характеристика заключается в том, что значение функции смешивания отлично от нуля для всех значений параметров по всей кривой.

Базис B-сплайна содержит базис Бернштейна как частный случай. Базис B-сплайна не является глобальным.

Кривая B-сплайна определяется как линейная комбинация контрольных точек Pi и базисной функции B-сплайна $N_ {i,}$ k (t), заданная как

$C (t) = \ sum_ {i = 0} ^ {n} P_ {i} N_ {i, k} (t),$ $n \ geq k-1,$ t epsilon[тк−1,тн+1]$t \: \ epsilon \: [ тк-1, тн + 1]$

Куда,

• {$p_ {i}$: i = 0, 1, 2… .n} — контрольные точки

• k — порядок отрезков полинома кривой B-сплайна. Порядок k означает, что кривая состоит из кусочно-полиномиальных отрезков степени k — 1,

• $N_ {i, k} (t)$ — «нормализованные функции смешивания B-сплайнов». Они описываются порядком k и неубывающей последовательностью действительных чисел, обычно называемой «последовательностью узлов».

{$p_ {i}$: i = 0, 1, 2… .n} — контрольные точки

k — порядок отрезков полинома кривой B-сплайна. Порядок k означает, что кривая состоит из кусочно-полиномиальных отрезков степени k — 1,

$N_ {i, k} (t)$ — «нормализованные функции смешивания B-сплайнов». Они описываются порядком k и неубывающей последовательностью действительных чисел, обычно называемой «последовательностью узлов».

$${t_ {i}: i = 0, ... n + K}$$

Функции N _i , k описываются следующим образом:

$$N_ {i, 1} (t) = \ left \ {\ begin {matrix} 1, & if \: u \: \ epsilon \: [t_ {i,} t_ {i + 1}) \\ 0 & Иначе \ end {matrix} \ right.$$

и если k> 1,

$$N_ {i, k} (t) = \ frac {t-t_ {i}} {t_ {i + k-1}} N_ {i, k-1} (t) + \ frac {t_ {i + k} -t} {t_ {i + k} - t_ {i + 1}} N_ {i + 1, k-1} (t)$$

а также

t epsilon[tk−1,tn+1) $$t \: \ epsilon \: [t_ {k-1}, t_ {n + 1})$$

Свойства кривой B-сплайна

Кривые B-сплайнов имеют следующие свойства:

Сумма базисных функций B-сплайна для любого значения параметра равна 1.

Каждая базовая функция положительна или равна нулю для всех значений параметров.

Каждая базовая функция имеет ровно одно максимальное значение, за исключением k = 1.

Максимальный порядок кривой равен числу вершин определяющего многоугольника.

Степень полинома B-сплайна не зависит от количества вершин определяющего многоугольника.

B-сплайн позволяет осуществлять локальный контроль над поверхностью кривой, поскольку каждая вершина влияет на форму кривой только в диапазоне значений параметров, где связанная с ней базисная функция отлична от нуля.

Кривая демонстрирует свойство уменьшения вариации.

Кривая обычно соответствует форме определяющего многоугольника.

Любое аффинное преобразование можно применить к кривой, применив ее к вершинам определяющего многоугольника.

Линия кривой внутри выпуклой оболочки его определяющего многоугольника.