Объекты представлены в виде набора поверхностей. 3D-представление объекта делится на две категории.
-
Граничные представления (B-повторы) — описывает трехмерный объект как набор поверхностей, которые отделяют внутреннюю часть объекта от окружающей среды.
-
Представления с пространственным разделением. Используются для описания внутренних свойств путем разделения пространственной области, содержащей объект, на набор небольших непересекающихся смежных тел (обычно кубов).
Граничные представления (B-повторы) — описывает трехмерный объект как набор поверхностей, которые отделяют внутреннюю часть объекта от окружающей среды.
Представления с пространственным разделением. Используются для описания внутренних свойств путем разделения пространственной области, содержащей объект, на набор небольших непересекающихся смежных тел (обычно кубов).
Наиболее часто используемое представление границ для трехмерного графического объекта — это набор поверхностных полигонов, которые охватывают внутреннюю часть объекта. Многие графические системы используют этот метод. Набор полигонов хранится для описания объекта. Это упрощает и ускоряет рендеринг поверхности и отображение объекта, поскольку все поверхности могут быть описаны с помощью линейных уравнений.
Поверхности многоугольника распространены в приложениях проектирования и твердотельного моделирования, поскольку их каркасное отображение может быть выполнено быстро, чтобы дать общее представление о структуре поверхности. Затем реалистичные сцены создаются путем интерполяции шаблонов затенения по поверхности многоугольника для освещения.
Таблицы полигонов
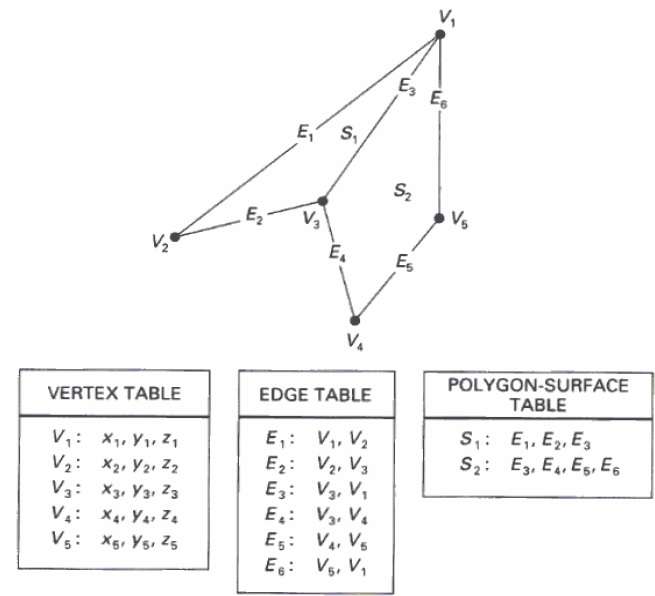
В этом методе поверхность задается набором координат вершин и связанных атрибутов. Как показано на следующем рисунке, существует пять вершин от v 1 до v 5 .
-
Каждая вершина хранит информацию о координатах x, y и z, которая представлена в таблице как v 1 : x 1 , y 1 , z 1 .
-
Таблица Edge используется для хранения информации о краях многоугольника. На следующем рисунке ребро E 1 лежит между вершиной v 1 и v 2, которое в таблице представлено как E 1 : v 1 , v 2 .
-
Таблица поверхностей полигонов хранит количество поверхностей, представленных в полигоне. На следующем рисунке поверхность S 1 покрыта ребрами E 1 , E 2 и E 3, которые могут быть представлены в таблице поверхностей многоугольников как S 1 : E 1 , E 2 и E 3 .
Каждая вершина хранит информацию о координатах x, y и z, которая представлена в таблице как v 1 : x 1 , y 1 , z 1 .
Таблица Edge используется для хранения информации о краях многоугольника. На следующем рисунке ребро E 1 лежит между вершиной v 1 и v 2, которое в таблице представлено как E 1 : v 1 , v 2 .
Таблица поверхностей полигонов хранит количество поверхностей, представленных в полигоне. На следующем рисунке поверхность S 1 покрыта ребрами E 1 , E 2 и E 3, которые могут быть представлены в таблице поверхностей многоугольников как S 1 : E 1 , E 2 и E 3 .
Плоскостные уравнения
Уравнение для плоской поверхности может быть выражено как —
Ax + By + Cz + D = 0
Где (x, y, z) — любая точка на плоскости, а коэффициенты A, B, C и D — это константы, описывающие пространственные свойства плоскости. Мы можем получить значения A, B, C и D, решая систему из трех уравнений плоскости, используя значения координат для трех неколлинеарных точек на плоскости. Предположим, что тремя вершинами плоскости являются (x 1 , y 1 , z 1 ), (x 2 , y 2 , z 2 ) и (x 3 , y 3 , z 3 ).
Решим следующие уравнения одновременности для отношений A / D, B / D и C / D. Вы получаете значения A, B, C и D.
(A / D) x 1 + (B / D) y 1 + (C / D) z 1 = -1
(A / D) x 2 + (B / D) y 2 + (C / D) z 2 = -1
(A / D) x 3 + (B / D) y 3 + (C / D) z 3 = -1
Чтобы получить вышеуказанные уравнения в форме определителя, примените правило Крамера к приведенным выше уравнениям.
A = \ begin {bmatrix} 1 & y_ {1} & z_ {1} \\ 1 & y_ {2} & z_ {2} \\ 1 & y_ {3} & z_ {3} \ end {bmatrix} B = \ begin {bmatrix} x_ {1} & 1 & z_ {1} \\ x_ {2} & 1 & z_ {2} \\ x_ {3} & 1 & z_ {3} \ end {bmatrix} C = \ begin {bmatrix} x_ {1} & y_ {1} & 1 \\ x_ {2} & y_ {2} & 1 \\ x_ {3} & y_ {3} & 1 \ end {bmatrix} D = — \ begin {bmatrix} x_ {1} & y_ {1} & z_ {1} \\ x_ {2} & y_ {2} & z_ {2} \\ x_ {3} & y_ {3} & z_ {3} \ end {bmatrix }
Для любой точки (x, y, z) с параметрами A, B, C и D можно сказать, что —
-
Ax + By + Cz + D means 0 означает, что точка не на плоскости.
-
Ax + By + Cz + D <0 означает, что точка находится внутри поверхности.
-
Ax + By + Cz + D> 0 означает, что точка находится за пределами поверхности.
Ax + By + Cz + D means 0 означает, что точка не на плоскости.
Ax + By + Cz + D <0 означает, что точка находится внутри поверхности.
Ax + By + Cz + D> 0 означает, что точка находится за пределами поверхности.
Сетки полигонов
Трехмерные поверхности и тела могут быть аппроксимированы набором многоугольных и линейных элементов. Такие поверхности называются многоугольными сетками . В полигональной сетке каждое ребро совместно используется не более чем двумя полигонами. Множество многоугольников или граней вместе образуют «кожу» объекта.
Этот метод может использоваться для представления широкого класса твердых тел / поверхностей в графике. Полигональная сетка может быть визуализирована с использованием скрытых алгоритмов удаления поверхности. Сетка многоугольника может быть представлена тремя способами: