Полигон — это упорядоченный список вершин, как показано на следующем рисунке. Для заливки полигонов определенными цветами необходимо определить пиксели, попадающие на границу многоугольника, и те, которые попадают внутрь многоугольника. В этой главе мы увидим, как мы можем заполнить полигоны, используя различные методы.
Алгоритм сканирования строки
Этот алгоритм работает путем пересечения линии сканирования с ребрами многоугольника и заполняет многоугольник между парами пересечений. Следующие шаги показывают, как работает этот алгоритм.
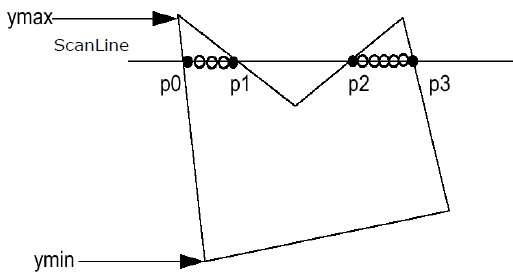
Шаг 1 — Узнайте Ymin и Ymax из данного многоугольника.
Шаг 2 — ScanLine пересекается с каждым ребром многоугольника от Ymin до Ymax. Назовите каждую точку пересечения многоугольника. Как показано на рисунке выше, они названы как p0, p1, p2, p3.
Шаг 3 — Сортировка точки пересечения в порядке возрастания координаты X, т. Е. (P0, p1), (p1, p2) и (p2, p3).
Шаг 4 — Заполните все те пары координат, которые находятся внутри полигонов и игнорируйте альтернативные пары.
Алгоритм заполнения потока
Иногда мы сталкиваемся с объектом, в котором мы хотим заполнить область и ее границу разными цветами. Мы можем рисовать такие объекты указанным цветом интерьера вместо поиска определенного цвета границы, как в алгоритме заполнения границ.
Вместо того чтобы полагаться на границу объекта, он опирается на цвет заливки. Другими словами, он заменяет цвет интерьера объекта цветом заливки. Когда больше нет пикселей исходного цвета интерьера, алгоритм завершается.
Еще раз, этот алгоритм основывается на методе заполнения пикселей с четырьмя соединениями или восьмью соединениями. Но вместо того, чтобы искать цвет границы, он ищет все смежные пиксели, которые являются частью интерьера.
Алгоритм граничного заполнения
Алгоритм заполнения границ работает как его имя. Этот алгоритм выбирает точку внутри объекта и начинает заполняться, пока не достигнет границы объекта. Цвет границы и цвет, который мы заполняем, должны быть разными, чтобы этот алгоритм работал.
В этом алгоритме мы предполагаем, что цвет границы одинаков для всего объекта. Алгоритм заполнения границ может быть реализован 4-мя связанными пикселями или 8-ю связанными пикселями.
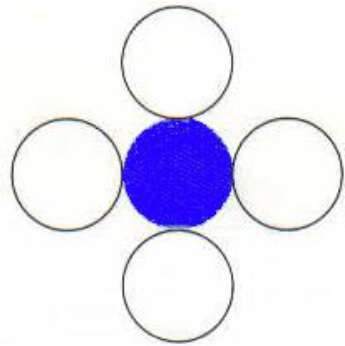
4-соединенный многоугольник
В этом методе используются 4 подключенных пикселя, как показано на рисунке. Мы помещаем пиксели выше, ниже, справа и слева от текущих пикселей, и этот процесс будет продолжаться, пока мы не найдем границу другого цвета.
Алгоритм
Шаг 1 — Инициализируйте значение начальной точки (seedx, seedy), fcolor и dcol.
Шаг 2 — Определите граничные значения многоугольника.
Шаг 3 — Проверьте, имеет ли текущая начальная точка цвет по умолчанию, затем повторите шаги 4 и 5, пока не будут достигнуты граничные пиксели.
If getpixel(x, y) = dcol then repeat step 4 and 5
Шаг 4 — Измените цвет по умолчанию с цветом заливки в начальной точке.
setPixel(seedx, seedy, fcol)
Шаг 5 — Рекурсивно выполните процедуру с четырьмя точками соседства.
FloodFill (seedx – 1, seedy, fcol, dcol) FloodFill (seedx + 1, seedy, fcol, dcol) FloodFill (seedx, seedy - 1, fcol, dcol) FloodFill (seedx – 1, seedy + 1, fcol, dcol)
Шаг 6 — Выход
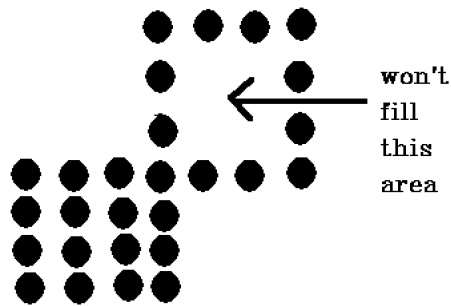
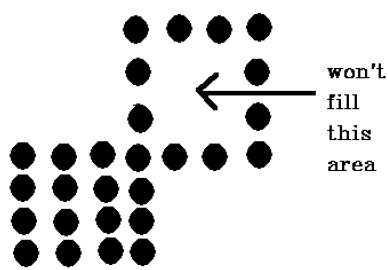
Есть проблема с этой техникой. Рассмотрим случай, показанный ниже, где мы пытались заполнить весь регион. Здесь изображение заполнено только частично. В таких случаях метод с 4-мя подключенными пикселями не может быть использован.
8-связанный многоугольник
В этом методе используются 8 подключенных пикселей, как показано на рисунке. Мы помещаем пиксели выше, ниже, справа и слева от текущих пикселей, как мы делали в 4-х подключенной технике.
В дополнение к этому мы также помещаем пиксели в диагонали, чтобы покрыть всю область текущего пикселя. Этот процесс будет продолжаться, пока мы не найдем границу с другим цветом.
Алгоритм
Шаг 1 — Инициализируйте значение начальной точки (seedx, seedy), fcolor и dcol.
Шаг 2 — Определите граничные значения многоугольника.
Шаг 3 — Проверьте, имеет ли текущая начальная точка цвет по умолчанию, затем повторите шаги 4 и 5, пока не будут достигнуты граничные пиксели
If getpixel(x,y) = dcol then repeat step 4 and 5
Шаг 4 — Измените цвет по умолчанию с цветом заливки в начальной точке.
setPixel(seedx, seedy, fcol)
Шаг 5 — Рекурсивно выполните процедуру с четырьмя точками соседства
FloodFill (seedx – 1, seedy, fcol, dcol) FloodFill (seedx + 1, seedy, fcol, dcol) FloodFill (seedx, seedy - 1, fcol, dcol) FloodFill (seedx, seedy + 1, fcol, dcol) FloodFill (seedx – 1, seedy + 1, fcol, dcol) FloodFill (seedx + 1, seedy + 1, fcol, dcol) FloodFill (seedx + 1, seedy - 1, fcol, dcol) FloodFill (seedx – 1, seedy - 1, fcol, dcol)
Шаг 6 — Выход
Техника с четырьмя подключенными пикселями не смогла заполнить область, как отмечено на следующем рисунке, что не случится с техникой с четырьмя связными.
Тест внутри-снаружи
Этот метод также известен как метод подсчета числа . При заполнении объекта нам часто необходимо определить, находится ли конкретная точка внутри объекта или вне его. Есть два метода, с помощью которых мы можем определить, находится ли конкретная точка внутри объекта или снаружи.
- Нечетное правило
- Правило ненулевого числа обмоток
Нечетное правило
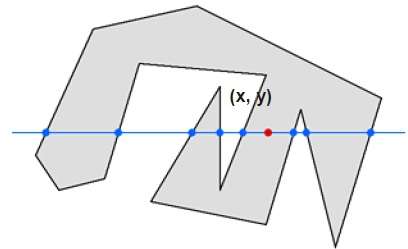
В этом методе мы будем считать пересечение ребер вдоль линии от любой точки (x, y) до бесконечности. Если число взаимодействий нечетно, то точка (x, y) является внутренней точкой; и если число взаимодействий четное, то точка (x, y) является внешней точкой. Следующий пример изображает эту концепцию.
Из приведенного выше рисунка видно, что из точки (x, y) число точек взаимодействия с левой стороны равно 5, а с правой стороны равно 3. С обоих концов число точек взаимодействия нечетно, поэтому точка считается внутри объекта.
Правило ненулевого числа обмоток
Этот метод также используется с простыми полигонами для проверки того, является ли данная точка внутренней или нет. Это можно понять с помощью булавки и резиновой ленты. Закрепите штифт на одном из краев многоугольника и свяжите в нем резиновую ленту, а затем вытяните резиновую ленту вдоль краев многоугольника.
Когда все края многоугольника покрыты резиновой лентой, проверьте штифт, который был зафиксирован в точке, подлежащей проверке. Если мы обнаружим хотя бы один ветер в точке, рассмотрим его внутри многоугольника, иначе мы можем сказать, что точка не находится внутри многоугольника.
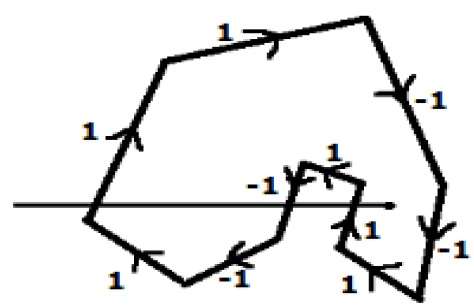
В другом альтернативном методе дайте указания всем ребрам многоугольника. Нарисуйте линию сканирования от тестируемой точки в направлении большей части левого направления X.
Задайте значение 1 для всех ребер, которые идут в направлении вверх, и все остальные -1 в качестве значений направления.
Проверьте значения направления края, от которого проходит линия сканирования, и суммируйте их.
Если общая сумма этого значения направления не равна нулю, то эта проверяемая точка является внутренней точкой, в противном случае это внешняя точка .
На приведенном выше рисунке мы суммируем значения направлений, из которых проходит линия сканирования, тогда сумма составляет 1 — 1 + 1 = 1; который ненулевой. Так что говорят, что это внутренняя точка.