Преобразование означает изменение некоторой графики во что-то другое путем применения правил. Мы можем иметь различные типы преобразований, такие как перемещение, масштабирование вверх или вниз, вращение, сдвиг и т. Д. Когда преобразование происходит в 2D-плоскости, это называется 2D-преобразованием.
Преобразования играют важную роль в компьютерной графике для изменения положения графики на экране и изменения их размера или ориентации.
Гомогенные координаты
Чтобы выполнить последовательность преобразований, таких как перевод с последующим вращением и масштабированием, нам необходимо выполнить последовательный процесс —
- Перевести координаты,
- Поверните переведенные координаты, а затем
- Масштабируйте повернутые координаты для завершения составного преобразования.
Чтобы сократить этот процесс, мы должны использовать матрицу преобразования 3 × 3 вместо матрицы преобразования 2 × 2. Чтобы преобразовать матрицу 2 × 2 в матрицу 3 × 3, мы должны добавить дополнительную фиктивную координату W.
Таким образом, мы можем представить точку 3 числами вместо 2 чисел, что называется Однородной системой координат . В этой системе мы можем представить все уравнения преобразования в матричном умножении. Любая декартова точка P (X, Y) может быть преобразована в однородные координаты с помощью P ‘(X h , Y h , h).
Перевод
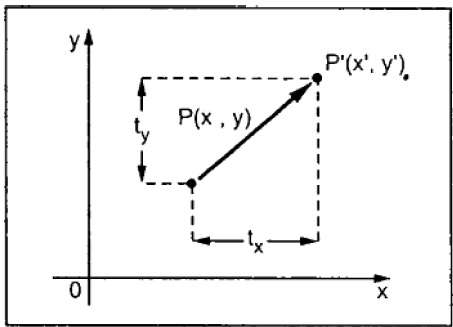
Перевод перемещает объект в другую позицию на экране. Вы можете перевести точку в 2D, добавив координату перемещения (t x , t y ) к исходной координате (X, Y), чтобы получить новую координату (X ‘, Y’).
Из приведенного выше рисунка вы можете написать, что —
X ‘= X + t x
Y ‘= Y + t y
Пара (t x , t y ) называется вектором перевода или вектором сдвига. Приведенные выше уравнения также могут быть представлены с использованием векторов столбцов.
$ P = \ frac {[X]} {[Y]} $ p ‘= $ \ frac {[X’]} {[Y ‘]} $ T = $ \ frac {[t_ {x}]} {[ t_ {у}]} $
Мы можем написать это как —
P ‘= P + T
вращение
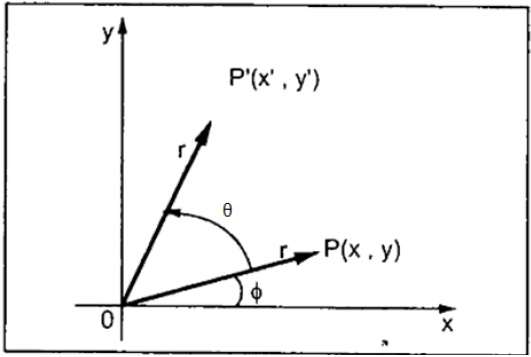
Вращаясь, мы поворачиваем объект на определенный угол θ (тета) от его начала. На следующем рисунке видно, что точка P (X, Y) расположена под углом φ от горизонтальной координаты X с расстоянием r от начала координат.
Предположим, вы хотите повернуть его на угол θ. Повернув его на новое место, вы получите новую точку P ‘(X’, Y ‘).
Используя стандартную тригонометрию, исходная координата точки P (X, Y) может быть представлена как —
$ X = r \, cos \, \ phi …… (1) $
$ Y = r \, sin \, \ phi …… (2) $
Таким же образом мы можем представить точку P ‘(X’, Y ‘) как —
$ {x} ‘= r \: cos \: \ left (\ phi \: + \: \ theta \ right) = r \: cos \: \ phi \: cos \: \ theta \: — \: r \ : sin \: \ phi \: sin \: \ theta ……. (3) $
$ {y} ‘= r \: sin \: \ left (\ phi \: + \: \ theta \ right) = r \: cos \: \ phi \: sin \: \ theta \: + \: r \ : sin \: \ phi \: cos \: \ theta ……. (4) $
Подставив уравнения (1) и (2) в (3) и (4) соответственно, получим
$ {x} ‘= x \: cos \: \ theta — \: y \: sin \: \ theta $
$ {y} ‘= x \: sin \: \ theta + \: y \: cos \: \ theta $
Представляя вышеприведенное уравнение в матричной форме,
$$ [X ‘Y’] = [XY] \ begin {bmatrix} cos \ theta & sin \ theta \\ −sin \ theta & cos \ theta \ end {bmatrix} ИЛИ $$
P ‘= P. р
Где R — матрица вращения
$$ R = \ begin {bmatrix} cos \ theta & sin \ theta \\ −sin \ theta & cos \ theta \ end {bmatrix} $$
Угол поворота может быть положительным и отрицательным.
Для положительного угла поворота мы можем использовать вышеуказанную матрицу вращения. Однако для поворота на отрицательный угол матрица изменится, как показано ниже —
$$ R = \ begin {bmatrix} cos (- \ theta) & sin (- \ theta) \\ -sin (- \ theta) & cos (- \ theta) \ end {bmatrix} $$
$$ = \ begin {bmatrix} cos \ theta & −sin \ theta \\ sin \ theta & cos \ theta \ end {bmatrix} \ left (\ потому что cos (- \ theta) = cos \ theta \; и \; грех (- \ theta) = −sin \ theta \ right) $$
пересчет
Чтобы изменить размер объекта, используется масштабное преобразование. В процессе масштабирования вы либо расширяете, либо сжимаете размеры объекта. Масштабирование может быть достигнуто путем умножения исходных координат объекта на коэффициент масштабирования, чтобы получить желаемый результат.
Предположим, что исходные координаты (X, Y), коэффициенты масштабирования (S X , S Y ) и полученные координаты (X ‘, Y’). Это может быть математически представлено, как показано ниже —
X ‘= X S X и Y ‘= Y. S Y
Коэффициент масштабирования S X , S Y масштабирует объект в направлении X и Y соответственно. Вышеприведенные уравнения также могут быть представлены в виде матрицы, как показано ниже:
$$ \ binom {X ‘} {Y’} = \ binom {X} {Y} \ begin {bmatrix} S_ {x} & 0 \\ 0 & S_ {y} \ end {bmatrix} $$
ИЛИ ЖЕ
P ‘= P. S
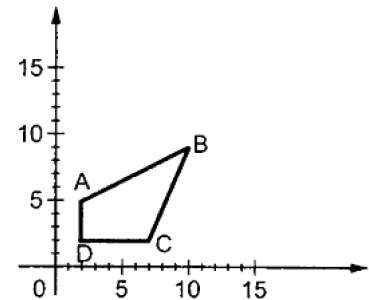
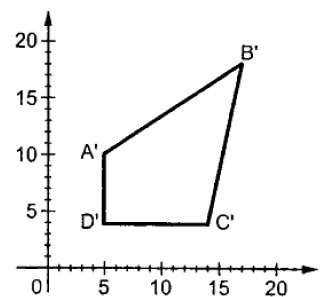
Где S — это масштабирующая матрица. Процесс масштабирования показан на следующем рисунке.
Если мы предоставим значения меньше 1 для коэффициента масштабирования S, то мы можем уменьшить размер объекта. Если мы предоставим значения больше 1, тогда мы сможем увеличить размер объекта.
отражение
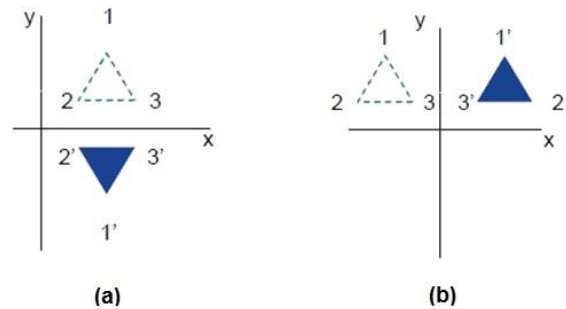
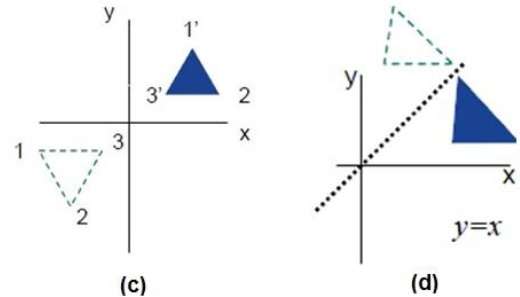
Отражение — это зеркальное отражение оригинального объекта. Другими словами, мы можем сказать, что это операция поворота на 180 °. При преобразовании отражения размер объекта не изменяется.
На следующих рисунках показаны отражения относительно осей X и Y и начала координат соответственно.
ножницы
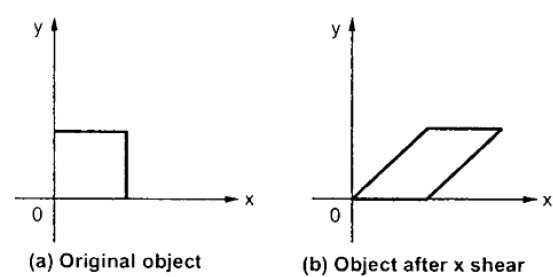
Преобразование, которое наклоняет форму объекта, называется сдвиговым преобразованием. Существуют две трансформации сдвига X-Shear и Y-Shear . Один сдвигает значения координат X, а другой сдвигает значения координат Y. Тем не мение; в обоих случаях только одна координата меняет свои координаты, а другая сохраняет свои значения. Стрижка также называется Skewing .
X-Shear
X-Shear сохраняет координату Y, и в координаты X вносятся изменения, в результате чего вертикальные линии наклоняются вправо или влево, как показано на рисунке ниже.
Матрица преобразования для X-Shear может быть представлена как —
$$ X_ {sh} = \ begin {bmatrix} 1 & shx & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \ end {bmatrix} $$
Y ‘= Y + Sh y . Икс
X ‘= X
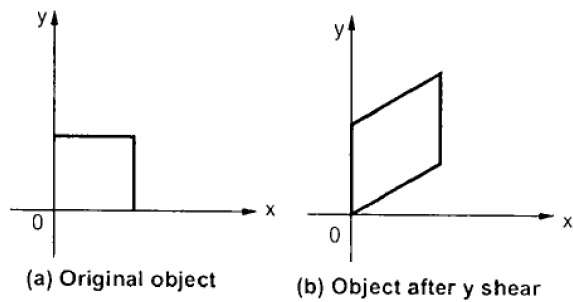
Y-сдвиг
Y-сдвиг сохраняет координаты X и изменяет координаты Y, в результате чего горизонтальные линии преобразуются в линии, которые имеют наклон вверх или вниз, как показано на следующем рисунке.
Y-сдвиг может быть представлен в матрице как —
$$ Y_ {sh} \ begin {bmatrix} 1 & 0 & 0 \\ shy & 1 & 0 \\ 0 & 0 & 1 \ end {bmatrix} $$
Х ‘= Х + Ш х . Y
Y ‘= Y
Композитная трансформация
Если за преобразованием плоскости T1 следует преобразование второй плоскости T2, то сам результат может быть представлен одним преобразованием T, которое представляет собой композицию T1 и T2, взятых в этом порядке. Это записывается как T = T1 ∙ T2.
Составное преобразование может быть достигнуто путем объединения матриц преобразования для получения комбинированной матрицы преобразования.
Комбинированная матрица —
[T] [X] = [X] [T1] [T2] [T3] [T4]…. [Тп]
Где [Ti] — любая комбинация
- Перевод
- пересчет
- сдвиг
- вращение
- отражение
Изменение порядка преобразования приведет к другим результатам, так как в общем случае умножение матриц не является кумулятивным, то есть [A]. [B] ≠ [B]. [A] и порядок умножения. Основная цель составления преобразований состоит в том, чтобы повысить эффективность, применяя одно составное преобразование к точке, а не применяя последовательность преобразований, одно за другим.
Например, чтобы повернуть объект вокруг произвольной точки (X p , Y p ), мы должны выполнить три шага: