Введение в контекстную грамматику

Определение — контекстно-свободная грамматика (CFG), состоящая из конечного набора правил грамматики, представляет собой четверку (N, T, P, S), где

• N представляет собой набор нетерминальных символов.

• T — это набор терминалов, где N ∩ T = NULL.

• P — это набор правил, P: N → (N ∪ T) * , т. Е. Левая часть производственного правила P имеет любой правый или левый контекст.

• S — начальный символ.

N представляет собой набор нетерминальных символов.

T — это набор терминалов, где N ∩ T = NULL.

P — это набор правил, P: N → (N ∪ T) * , т. Е. Левая часть производственного правила P имеет любой правый или левый контекст.

S — начальный символ.

пример

• Грамматика ({A}, {a, b, c}, P, A), P: A → aA, A → abc.
• Грамматика ({S, a, b}, {a, b}, P, S), P: S → aSa, S → bSb, S → ε
• Грамматика ({S, F}, {0, 1}, P, S), P: S → 00S | 11F, F → 00F | ε

Генерация дерева деривации

Дерево деривации или дерево разбора — это упорядоченное корневое дерево, которое графически представляет семантическую информацию в виде строки, полученной из контекстно-свободной грамматики.

Техника Представления

• Корневая вершина — должна быть помечена начальным символом.

• Вершина — помечена нетерминальным символом.

• Листья — помечены терминальным символом или ε.

Корневая вершина — должна быть помечена начальным символом.

Вершина — помечена нетерминальным символом.

Листья — помечены терминальным символом или ε.

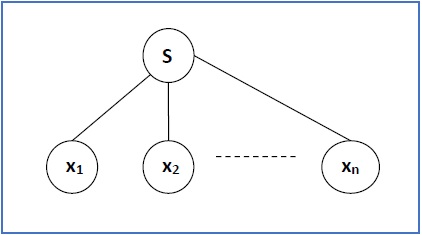
Если S → x ₁ x ₂ …… x _n является правилом производства в CFG, то дерево разбора / дерево деривации будет выглядеть следующим образом:

Существует два разных подхода для построения деривационного дерева:

Нисходящий подход —

• Начинается с начального символа S

• Спускается к листьям дерева, используя продукцию

Начинается с начального символа S

Спускается к листьям дерева, используя продукцию

Подход снизу вверх —

• Начинается с листьев дерева

• Идет вверх к корню, который является начальным символом S

Начинается с листьев дерева

Идет вверх к корню, который является начальным символом S

Вывод или урожайность дерева

Деривация или выход дерева разбора — это последняя строка, полученная путем объединения меток листьев дерева слева направо, игнорируя значения Null. Однако, если все листья равны нулю, деривация равна нулю.

пример

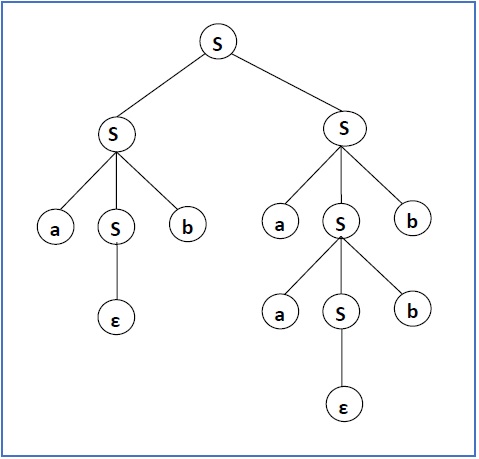
Пусть CFG {N, T, P, S} будет

N = {S}, T = {a, b}, начальный символ = S, P = S → SS | aSb | ε

Одним из производных от вышеупомянутого CFG является «abaabb»

S → SS → aSbS → abS → abaSb → abaaSbb → abaabb

Форма предложения и Дерево частичного деривации

Частичное дерево деривации является поддеревом дерева деривации / дерева разбора, так что либо все его дочерние элементы находятся в поддереве, либо ни один из них не находится в поддереве.

пример

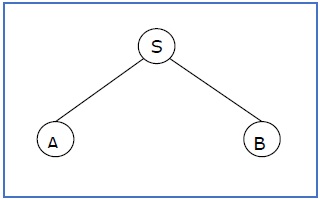
Если в любом CFG производства —

S → AB, A → aaA | ε, B → Bb | ε

Частичное дерево деривации может быть следующим:

Если дерево частичного деривации содержит корень S, оно называется формой предложения . Вышеуказанное поддерево также в форме предложения.

Самый левый и самый правый вывод строки

• Самый левый вывод — самый левый вывод получается путем применения производства к самой левой переменной на каждом шаге.

• Крайний правый вывод — Крайний правый вывод получается путем применения производного к самой правой переменной на каждом шаге.

Самый левый вывод — самый левый вывод получается путем применения производства к самой левой переменной на каждом шаге.

Крайний правый вывод — Крайний правый вывод получается путем применения производного к самой правой переменной на каждом шаге.

пример

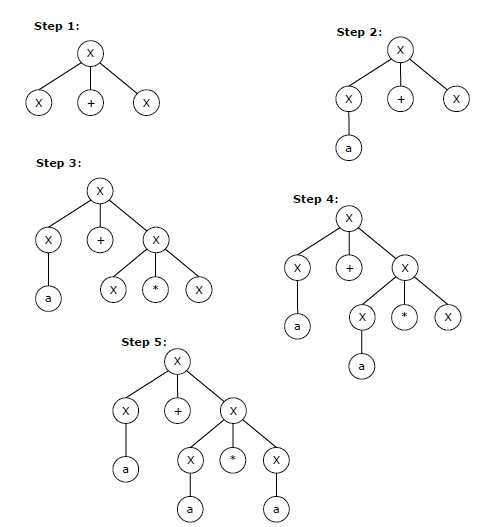
Пусть любой набор правил производства в CFG будет

X → X + X | X * X | X |

над алфавитом {а}.

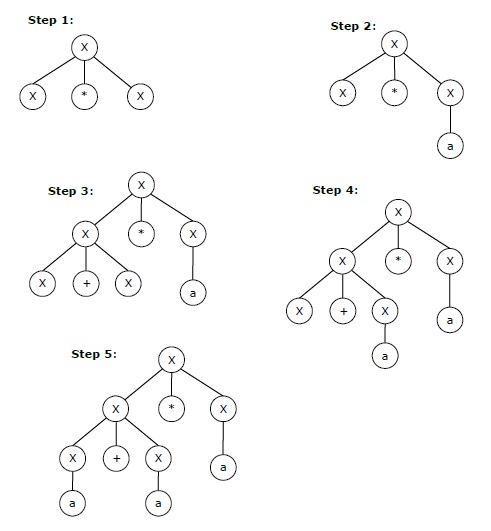
Крайний левый вывод для строки «a + a * a» может быть —

X → X + X → a + X → a + X * X → a + a * X → a + a * a

Пошаговое извлечение вышеуказанной строки показано ниже:

Самый правый вывод для приведенной выше строки «a + a * a» может быть —

X → X * X → X * a → X + X * a → X + a * a → a + a * a

Пошаговое извлечение вышеуказанной строки показано ниже:

Левая и правая рекурсивные грамматики

В не зависящей от контекста грамматике G , если существует произведение в форме X → Xa, где X — нетерминал, а ‘a’ — строка терминалов, это называется леворекурсивным произведением . Грамматика с левой рекурсивной продукцией называется левой рекурсивной грамматикой .

И если в не зависящей от контекста грамматике G , если есть произведение, имеет вид X → aX, где X — нетерминал, а ‘a’ — строка терминалов, это называется правильным рекурсивным произведением . Правильная рекурсивная грамматика называется правильной рекурсивной грамматикой .