В NDFA для определенного входного символа машина может перейти в любую комбинацию состояний в машине. Другими словами, точное состояние, в которое перемещается машина, не может быть определено. Следовательно, он называется недетерминированным автоматом . Поскольку оно имеет конечное число состояний, машина называется недетерминированным конечным автоматом или недетерминированным конечным автоматом .
Формальное определение NDFA
NDFA может быть представлен 5-кортежем (Q, ∑, δ, q 0 , F), где —
-
Q — конечное множество состояний.
-
∑ — это конечный набор символов, называемых алфавитами.
-
δ — функция перехода, где δ: Q × ∑ → 2 Q
(Здесь набор мощности Q (2 Q ) был взят, потому что в случае NDFA из состояния может произойти переход к любой комбинации состояний Q)
-
q 0 — начальное состояние, из которого обрабатывается любой вход (q 0 ∈ Q).
-
F — множество конечных состояний / состояний Q (F ⊆ Q).
Q — конечное множество состояний.
∑ — это конечный набор символов, называемых алфавитами.
δ — функция перехода, где δ: Q × ∑ → 2 Q
(Здесь набор мощности Q (2 Q ) был взят, потому что в случае NDFA из состояния может произойти переход к любой комбинации состояний Q)
q 0 — начальное состояние, из которого обрабатывается любой вход (q 0 ∈ Q).
F — множество конечных состояний / состояний Q (F ⊆ Q).
Графическое представление NDFA: (так же, как DFA)
NDFA представлен орграфами, которые называются диаграммой состояний.
- Вершины представляют состояния.
- Дуги, помеченные входным алфавитом, показывают переходы.
- Начальное состояние обозначается пустой единственной входящей дугой.
- Конечное состояние обозначено двойными кружками.
пример
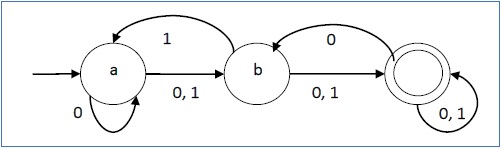
Пусть недетерминированный конечный автомат будет →
- Q = {a, b, c}
- ∑ = {0, 1}
- q 0 = {а}
- F = {c}
Функция перехода δ, как показано ниже —
| Современное состояние | Следующее состояние для ввода 0 | Следующее состояние для ввода 1 |
|---|---|---|
| а, б | б | |
| б | с | а, с |
| с | До нашей эры | с |
Его графическое представление будет следующим:
ДФА против НДФА
В следующей таблице перечислены различия между DFA и NDFA.
| DFA | NDFA |
|---|---|
| Переход из состояния в одно конкретное следующее состояние для каждого входного символа. Следовательно это называется детерминированным . | Переход из состояния может быть в несколько следующих состояний для каждого входного символа. Следовательно это называется недетерминированным . |
| Пустые строковые переходы не видны в DFA. | NDFA разрешает переходы пустой строки. |
| Отклонение разрешено в DFA | В NDFA откат не всегда возможен. |
| Требуется больше места. | Требует меньше места. |
| DFA принимает строку, если она переходит в конечное состояние. | NDFA принимает строку, если хотя бы один из всех возможных переходов заканчивается в конечном состоянии. |
Акцепторы, классификаторы и преобразователи
Акцептор (Распознаватель)
Автомат, который вычисляет булеву функцию, называется акцептором . Все состояния акцептора либо принимают, либо отклоняют введенные ему входные данные.
классификатор
Классификатор имеет более двух конечных состояний и выдает один выход при его завершении.
преобразователь
Автомат, который производит выходные данные на основе текущего входа и / или предыдущего состояния, называется преобразователем . Преобразователи могут быть двух типов —
-
Мили Машина — выход зависит как от текущего состояния и текущего ввода.
-
Moore Machine — Выход зависит только от текущего состояния.
Мили Машина — выход зависит как от текущего состояния и текущего ввода.
Moore Machine — Выход зависит только от текущего состояния.
Приемлемость DFA и NDFA
DFA / NDFA принимает строку, если DFA / NDFA, начиная с начального состояния, заканчивается после полного чтения строки в состоянии принятия (любом из конечных состояний).
Строка S принимается DFA / NDFA (Q, ∑, δ, q 0 , F), если
δ * (q 0 , S) ∈ F
Язык L принятый DFA / NDFA:
{S | S ∈ ∑ * и δ * (q 0 , S) ∈ F}
Строка S ′ не принимается DFA / NDFA (Q, ∑, δ, q 0 , F), если
δ * (q 0 , S ′) ∉ F
Язык L ′ не принят DFA / NDFA (дополнение к принятому языку L)
{S | S ∈ ∑ * и δ * (q 0 , S) ∉ F}
пример
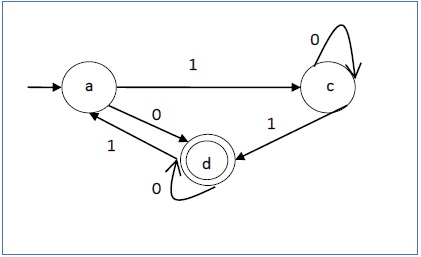
Давайте рассмотрим DFA, показанный на рисунке 1.3. Из DFA, приемлемые строки могут быть получены.
Строки, принятые вышеуказанным DFA: {0, 00, 11, 010, 101, ………..}
Строки, не принятые вышеуказанным DFA: {1, 011, 111, ……..}