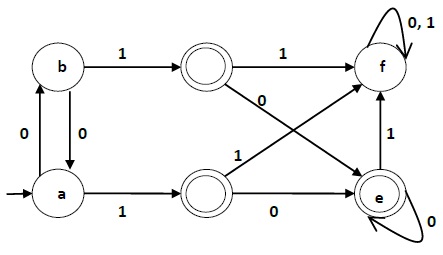
Вход — DFA
Вывод — минимизированный DFA
Шаг 1 — Нарисуйте таблицу для всех пар состояний (Q i , Q j ), не обязательно связанных напрямую [Все изначально не отмечены]
Шаг 2 — Рассмотрим каждую пару состояний (Q i , Q j ) в DFA, где Q i ∈ F и Q j ∉ F, или наоборот, и отметьте их. [Здесь F — множество конечных состояний]
Шаг 3 — Повторяйте этот шаг, пока мы больше не сможем помечать состояния —
Если есть немаркированная пара (Q i , Q j ), отметьте ее, если пара {δ (Q i , A), δ (Q i , A)} отмечена для некоторого входного алфавита.
Шаг 4 — Объедините все непомеченные пары (Q i , Q j ) и сделайте их единым состоянием в сокращенном DFA.
пример
Давайте используем алгоритм 2, чтобы минимизировать DFA, показанный ниже.
Шаг 1 — Нарисуем таблицу для всех пар состояний.
| б | с | d | е | е | ||
| б | ||||||
| с | ||||||
| d | ||||||
| е | ||||||
| е |
Шаг 2 — Отметим пары состояний.
| б | с | d | е | е | ||
| б | ||||||
| с | ✔ | ✔ | ||||
| d | ✔ | ✔ | ||||
| е | ✔ | ✔ | ||||
| е | ✔ | ✔ | ✔ |
Шаг 3 — Мы попытаемся пометить пары состояний, отмеченные зеленым цветом, транзитивно. Если мы введем 1 в состояние «a» и «f», он перейдет в состояние «c» и «f» соответственно. (c, f) уже отмечен, поэтому мы будем отмечать пару (a, f). Теперь мы вводим 1 в состояние «b» и «f»; он перейдет в состояние «d» и «f» соответственно. (d, f) уже отмечен, поэтому мы будем отмечать пару (b, f).
| б | с | d | е | е | ||
| б | ||||||
| с | ✔ | ✔ | ||||
| d | ✔ | ✔ | ||||
| е | ✔ | ✔ | ||||
| е | ✔ | ✔ | ✔ | ✔ | ✔ |
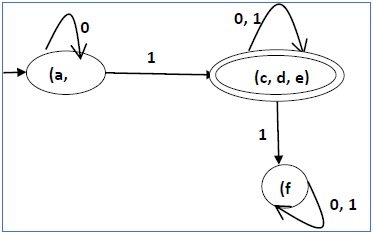
После шага 3 у нас есть комбинации состояний {a, b} {c, d} {c, e} {d, e}, которые не отмечены.
Мы можем рекомбинировать {c, d} {c, e} {d, e} в {c, d, e}
Следовательно, мы получили два комбинированных состояния как — {a, b} и {c, d, e}
Таким образом, окончательный свернутый DFA будет содержать три состояния {f}, {a, b} и {c, d, e}
Минимизация DFA с использованием теоремы об эквивалентности
Если X и Y — два состояния в DFA, мы можем объединить эти два состояния в {X, Y}, если они не различимы. Два состояния различимы, если есть хотя бы одна строка S, так что одно из δ (X, S) и δ (Y, S) принимает, а другое не принимает. Следовательно, DFA минимален тогда и только тогда, когда все состояния различимы.
Алгоритм 3
Шаг 1 — Все состояния Q разделены на два раздела — конечные состояния и неконечные состояния и обозначены P 0 . Все состояния в разделе имеют 0- й эквивалент. Возьмите счетчик k и инициализируйте его 0.
Шаг 2. Увеличьте k на 1. Для каждого разбиения в P k разделите состояния в P k на два разбиения, если они различимы по k. Два состояния в этом разделе X и Y являются k-различимыми, если существует вход S такой, что δ (X, S) и δ (Y, S) являются (k-1) -различимыми.
Шаг 3 — Если P k ≠ P k-1 , повторите шаг 2, в противном случае перейдите к шагу 4.
Шаг 4 — Объедините k- е эквивалентные наборы и сделайте их новыми состояниями сокращенного DFA.
пример
Давайте рассмотрим следующий DFA —
| Q | δ (д, 0) | δ (д, 1) |
|---|---|---|
| б | с | |
| б | d | |
| с | е | е |
| d | е | е |
| е | е | е |
| е | е | е |
Давайте применим вышеупомянутый алгоритм к вышеупомянутому DFA —
- P 0 = {(c, d, e), (a, b, f)}
- P 1 = {(c, d, e), (a, b), (f)}
- P 2 = {(c, d, e), (a, b), (f)}
Следовательно, P 1 = P 2 .
В сокращенном DFA есть три состояния. Уменьшенный DFA выглядит следующим образом —