Согласно Ноаму Хомоски, существует четыре типа грамматик — Тип 0, Тип 1, Тип 2 и Тип 3. В следующей таблице показано, как они отличаются друг от друга —
| Тип грамматики | Грамматика принята | Язык принят | Автомат |
|---|---|---|---|
| Тип 0 | Неограниченная грамматика | Рекурсивно перечислимый язык | Машина Тьюринга |
| Тип 1 | Контекстно-зависимая грамматика | Контекстно-зависимый язык | Линейно-ограниченный автомат |
| Тип 2 | Контекстная грамматика | Контекстно-свободный язык | Pushdown автомат |
| Тип 3 | Обычная грамматика | Обычный язык | Конечный автомат |
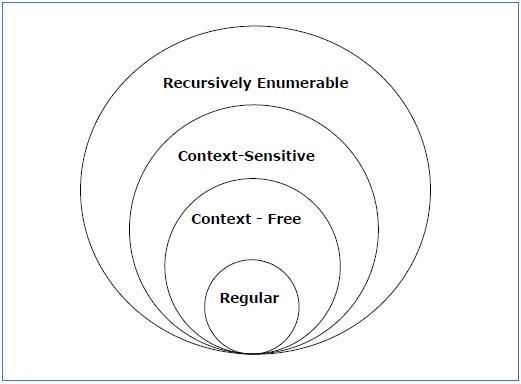
Посмотрите на следующую иллюстрацию. Он показывает объем каждого типа грамматики —
Тип — 3 грамматики
Грамматики типа 3 генерируют обычные языки. Грамматики типа 3 должны иметь один нетерминал с левой стороны и правую сторону, состоящую из одного терминала или одного терминала, за которым следует один нетерминал.
Произведения должны быть в форме X → a или X → aY
где X, Y ∈ N (нетерминал)
и a ∈ T (терминал)
Правило S → ε допустимо, если S не появляется справа от какого-либо правила.
пример
X → ε X → a | aY Y → b
Тип — 2 грамматики
Грамматики типа 2 генерируют языки без контекста.
Произведения должны быть в форме A → γ
где A ∈ N (нетерминал)
и γ ∈ (T ∪ N) * (строка терминалов и нетерминалов).
Эти языки, генерируемые этими грамматиками, распознаются недетерминированным автоматом.
пример
S → X a X → a X → aX X → abc X → ε
Тип — 1 грамматика
Грамматики типа 1 генерируют контекстно-зависимые языки. Продукция должна быть в форме
α A β → α γ β
где A ∈ N (нетерминал)
и α, β, γ ∈ (T ∪ N) * (строки терминалов и нетерминалов)
Строки α и β могут быть пустыми, но γ должна быть непустой.
Правило S → ε допустимо, если S не появляется справа от какого-либо правила. Языки, генерируемые этими грамматиками, распознаются линейным ограниченным автоматом.
пример
AB → AbBc A → bcA B → b
Тип — 0 Грамматика
Грамматики типа 0 генерируют рекурсивно перечислимые языки. Производства не имеют ограничений. Это грамматика любой фазовой структуры, включая все формальные грамматики.
Они генерируют языки, которые распознаются машиной Тьюринга.
Произведения могут быть в форме α → β, где α — строка терминалов и нетерминалов, по крайней мере, с одним нетерминалом, и α не может быть нулевым. β — цепочка терминалов и нетерминалов.