Существует два разных способа определения приемлемости КПК.
Окончательная государственная приемлемость
В приемлемости конечного состояния КПК принимает строку, когда после прочтения всей строки КПК находится в конечном состоянии. Из начального состояния мы можем делать ходы, которые заканчиваются в конечном состоянии с любыми значениями стека. Значения стека не имеют значения, пока мы не окажемся в конечном состоянии.
Для КПК (Q, ∑, S, δ, q 0 , I, F) язык, принятый множеством конечных состояний F, равен —
L (PDA) = {w | (q 0 , w, I) ⊢ * (q, ε, x), q ∈ F}
для любой строки входного стека x .
Приемлемость пустого стека
Здесь КПК принимает строку, когда после чтения всей строки КПК опустошил свой стек.
Для КПК (Q, ∑, S, δ, q 0 , I, F) язык, принятый пустым стеком, равен —
L (PDA) = {w | (q 0 , w, I) ⊢ * (q, ε, ε), q ∈ Q}
пример
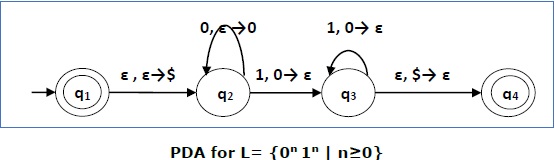
Построить КПК, который принимает L = {0 n 1 n | n ≥ 0}
Решение
Этот язык принимает L = {ε, 01, 0011, 000111, ………………………..}
Здесь, в этом примере, число «a» и «b» должно быть одинаковым.
-
Сначала мы помещаем специальный символ «$» в пустой стек.
-
Затем в состоянии q 2 , если мы сталкиваемся с вводом 0 и top равен Null, мы помещаем 0 в стек. Это может повторяться. И если мы встретим ввод 1 и top равен 0, мы вытолкнем это 0.
-
Затем в состоянии q 3 , если мы сталкиваемся с входом 1 и top равен 0, мы выталкиваем это 0. Это также может повторяться. И если мы встретим ввод 1 и top равен 0, мы вытолкнем верхний элемент.
-
Если в верхней части стека встречается специальный символ ‘$’, он выталкивается и, наконец, переходит в принимающее состояние q 4 .
Сначала мы помещаем специальный символ «$» в пустой стек.
Затем в состоянии q 2 , если мы сталкиваемся с вводом 0 и top равен Null, мы помещаем 0 в стек. Это может повторяться. И если мы встретим ввод 1 и top равен 0, мы вытолкнем это 0.
Затем в состоянии q 3 , если мы сталкиваемся с входом 1 и top равен 0, мы выталкиваем это 0. Это также может повторяться. И если мы встретим ввод 1 и top равен 0, мы вытолкнем верхний элемент.
Если в верхней части стека встречается специальный символ ‘$’, он выталкивается и, наконец, переходит в принимающее состояние q 4 .
пример
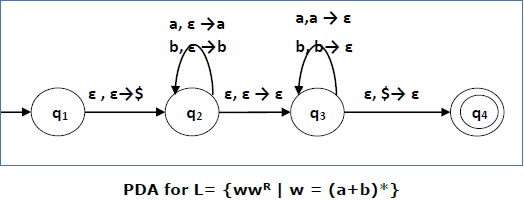
Построить КПК, который принимает L = {ww R | w = (a + b) *}
Решение
Сначала мы помещаем специальный символ «$» в пустой стек. В состоянии q 2 w читается. В состоянии q 3 каждый 0 или 1 выталкивается, когда он соответствует входу. Если задан какой-либо другой вход, КПК перейдет в мертвое состояние. Когда мы достигаем этого специального символа ‘$’, мы переходим в принимающее состояние q 4 .