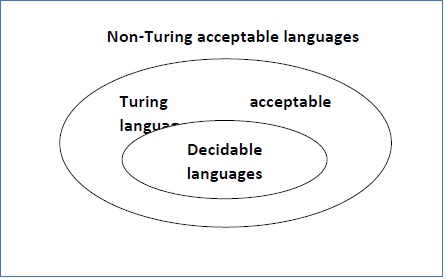
Язык называется Decidable или Recursive, если есть машина Тьюринга, которая принимает и останавливает каждую входную строку w . Каждый решаемый язык является приемлемым по Тьюрингу.
Решение проблемы P разрешимо, если язык L всех экземпляров yes для P разрешим.
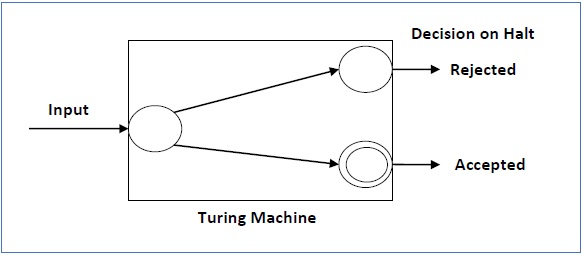
Для разрешимого языка, для каждой входной строки, TM останавливается либо в состоянии принятия, либо в состоянии отказа, как показано на следующей диаграмме —
Пример 1
Узнайте, разрешима ли следующая проблема —
Является ли число ‘m’ простым?
Решение
Простые числа = {2, 3, 5, 7, 11, 13, ………… ..}
Разделите число «m» на все числа от «2» до «√m», начиная с «2».
Если какое-либо из этих чисел выдает остаток ноль, то он переходит в «Отклоненное состояние», в противном случае он переходит в «Принятое состояние». Таким образом, здесь ответ может быть «Да» или «Нет».
Следовательно, это разрешимая проблема.
Пример 2
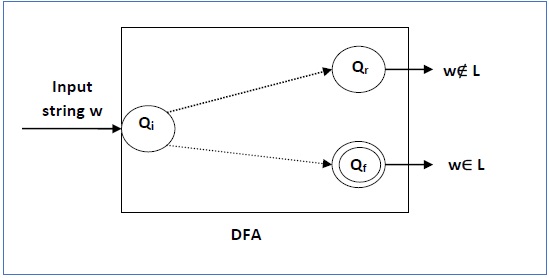
Учитывая регулярный язык L и строку w , как мы можем проверить, если w ∈ L ?
Решение
Возьмите DFA, который принимает L, и проверьте, принят ли w
Некоторые более решаемые проблемы —
- Принимает ли DFA пустой язык?
- Является ли L 1 ∩ L 2 = ∅ для регулярных множеств?
Примечание —
Если язык L разрешим, то его дополнение L ‘ также разрешимо
Если язык разрешим, то для него есть перечислитель.