Мы можем использовать конструкцию Томпсона, чтобы найти конечный автомат по регулярному выражению. Мы сведем регулярное выражение к наименьшим регулярным выражениям и преобразуем их в NFA и, наконец, в DFA.
Вот некоторые основные выражения RA:
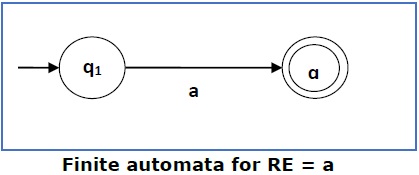
Случай 1 — Для регулярного выражения ‘a’ мы можем построить следующую FA —
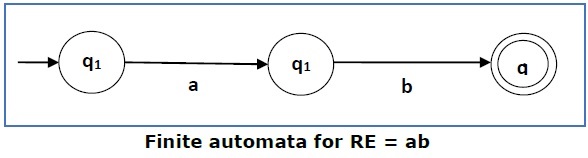
Случай 2 — Для регулярного выражения ‘ab’ мы можем построить следующую FA —
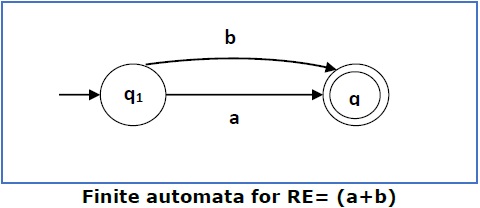
Случай 3 — Для регулярного выражения (a + b) мы можем построить следующую FA —
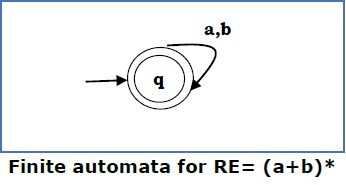
Случай 4 — Для регулярного выражения (a + b) * мы можем построить следующую FA —
метод
Шаг 1 Создайте NFA с нулевыми движениями из заданного регулярного выражения.
Шаг 2 Удалите нулевой переход из NFA и преобразуйте его в эквивалентный DFA.
проблема
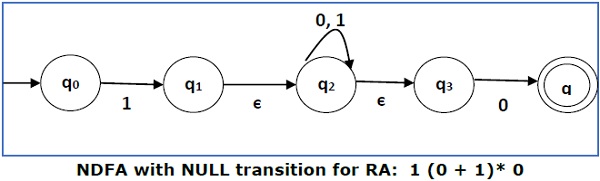
Преобразовать следующий RA в его эквивалентный DFA — 1 (0 + 1) * 0
Решение
Мы объединяем три выражения «1», «(0 + 1) *» и «0»
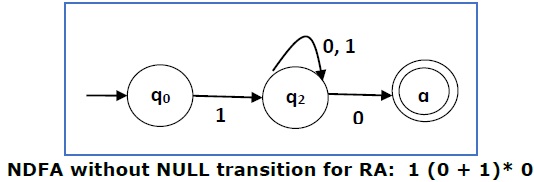
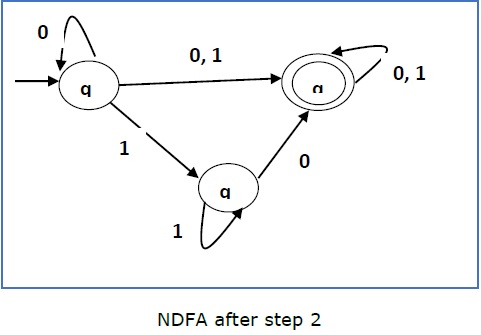
Теперь мы удалим ε- переходы. После того как мы удалим ε- переходы из NDFA, мы получим следующее —
Это NDFA, соответствующий RE — 1 (0 + 1) * 0. Если вы хотите преобразовать его в DFA, просто примените метод преобразования NDFA в DFA, описанный в главе 1.
Конечные автоматы с нулевыми ходами (NFA-ε)
Конечный автомат с нулевыми ходами (FA-ε) проходит не только после ввода входных данных из набора алфавитов, но и без какого-либо входного символа. Этот переход без ввода называется нулевым ходом .
NFA-ε формально представлен 5-кортежем (Q, ∑, δ, q 0 , F), состоящим из
-
Q — конечное множество состояний
-
∑ — конечный набор входных символов
-
δ — функция перехода δ: Q × (∑ ∪ {ε}) → 2 Q
-
q 0 — начальное состояние q 0 ∈ Q
-
F — множество конечных состояний / состояний Q (F⊆Q).
Q — конечное множество состояний
∑ — конечный набор входных символов
δ — функция перехода δ: Q × (∑ ∪ {ε}) → 2 Q
q 0 — начальное состояние q 0 ∈ Q
F — множество конечных состояний / состояний Q (F⊆Q).
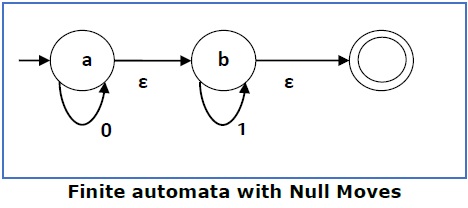
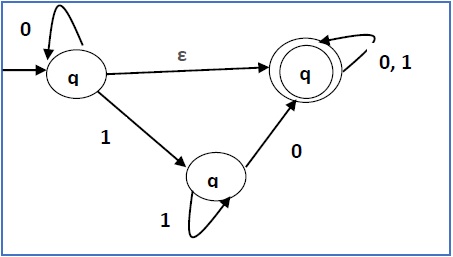
Выше (FA-ε) принимает набор строк — {0, 1, 01}
Удаление нулевых ходов из конечных автоматов
Если в NDFA есть move-перемещение между вершиной X к вершине Y, мы можем удалить его, используя следующие шаги:
- Найти все исходящие ребра от Y.
- Скопируйте все эти ребра, начиная с X, не меняя метки ребер.
- Если X — начальное состояние, сделайте Y также начальным состоянием.
- Если Y — конечное состояние, сделайте X также конечным состоянием.
проблема
Преобразуйте следующие NFA-ε в NFA без нулевого хода.
Решение
Шаг 1 —
Здесь ε-переход находится между q 1 и q 2 , поэтому пусть q 1 является X, а q f является Y.
Здесь исходящие ребра из q f равны q f для входов 0 и 1.
Шаг 2 —
Теперь мы скопируем все эти ребра из q 1, не меняя ребер из q f, и получим следующий FA —
Шаг 3 —
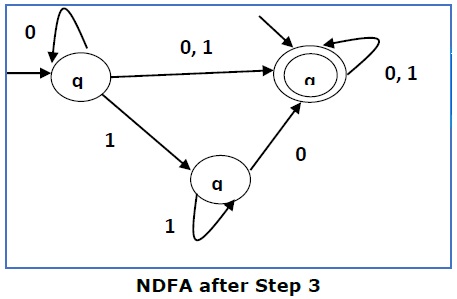
Здесь q 1 — начальное состояние, поэтому мы делаем q f также начальным состоянием.
Таким образом, ФА становится
Шаг 4 —
Здесь q f — конечное состояние, поэтому мы делаем q 1 также конечным состоянием.
Таким образом, ФА становится