Чтобы найти регулярное выражение конечного автомата, мы используем теорему Ардена вместе со свойствами регулярных выражений.
Заявление —
Пусть P и Q два регулярных выражения.
Если P не содержит нулевую строку, то R = Q + RP имеет единственное решение, которое R = QP *
Доказательство —
R = Q + (Q + RP) P [После помещения значения R = Q + RP]
= Q + QP + RPP
Когда мы снова и снова ставим значение R рекурсивно, мы получаем следующее уравнение:
R = Q + QP + QP 2 + QP 3 … ..
R = Q (ε + P + P 2 + P 3 +….)
R = QP * [Как P * представляет (ε + P + P2 + P3 +….)]
Следовательно, доказано.
Предположения для применения теоремы Ардена
- Диаграмма переходов не должна иметь переходов NULL
- Должно быть только одно начальное состояние
метод
Шаг 1 — Создайте уравнения в виде следующей формы для всех состояний DFA, имеющих n состояний с начальным состоянием q 1 .
q 1 = q 1 R 11 + q 2 R 21 +… + q n R n1 + ε
q 2 = q 1 R 12 + q 2 R 22 +… + q n R n2
…………………………
…………………………
…………………………
…………………………
q n = q 1 R 1n + q 2 R 2n +… + q n R nn
R ij представляет множество меток ребер от q i до q j , если такого ребра не существует, то R ij = ∅
Шаг 2 — Решите эти уравнения, чтобы получить уравнение для конечного состояния в терминах R ij
проблема
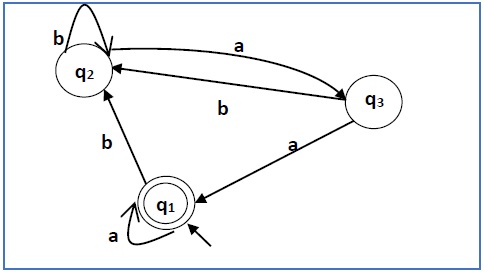
Построить регулярное выражение, соответствующее автоматам, приведенным ниже —
Решение —
Здесь начальное состояние и конечное состояние q 1 .
Уравнения для трех состояний q1, q2 и q3 следующие:
q 1 = q 1 a + q 3 a + ε (перемещение ε происходит потому, что q1 является начальным состоянием 0
q 2 = q 1 b + q 2 b + q 3 b
q 3 = q 2 a
Теперь мы будем решать эти три уравнения —
q 2 = q 1 b + q 2 b + q 3 b
= q 1 b + q 2 b + (q 2 a) b (подставляя значение q 3 )
= q 1 b + q 2 (b + ab)
= q 1 b (b + ab) * (применение теоремы Ардена)
q 1 = q 1 a + q 3 a + ε
= q 1 a + q 2 aa + ε (Подставляя значение q 3 )
= q 1 a + q 1 b (b + ab *) aa + ε (Подставляя значение q 2 )
= q 1 (a + b (b + ab) * aa) + ε
= ε (a + b (b + ab) * aa) *
= (a + b (b + ab) * aa) *
Следовательно, регулярное выражение имеет вид (a + b (b + ab) * aa) *.
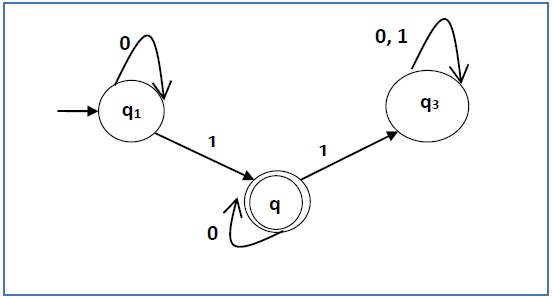
проблема
Построить регулярное выражение, соответствующее автоматам, приведенным ниже —
Решение —
Здесь начальное состояние q 1, а конечное состояние q 2
Теперь запишем уравнения —
q 1 = q 1 0 + ε
q 2 = q 1 1 + q 2 0
q 3 = q 2 1 + q 3 0 + q 3 1
Теперь мы будем решать эти три уравнения —
q 1 = ε0 * [As, εR = R]
Итак, q 1 = 0 *
q 2 = 0 * 1 + q 2 0
Итак, q 2 = 0 * 1 (0) * [по теореме Ардена]
Следовательно, регулярное выражение 0 * 10 *.