Пусть X = (Q x , ∑, δ x , q 0 , F x ) NDFA, который принимает язык L (X). Мы должны спроектировать эквивалентный DFA Y = (Q y , ∑, δ y , q 0 , F y ) такой, что L (Y) = L (X) . Следующая процедура преобразует NDFA в эквивалентный DFA —
Алгоритм
Вход — NDFA
Выход — эквивалент DFA
Шаг 1 — Создать таблицу состояний из заданного NDFA.
Шаг 2 — Создайте пустую таблицу состояний под возможными входными алфавитами для эквивалентного DFA.
Шаг 3 — Отметьте начальное состояние DFA как q0 (то же самое, что и NDFA).
Шаг 4 — Узнайте комбинацию состояний {Q 0 , Q 1 , …, Q n } для каждого возможного входного алфавита.
Шаг 5 — Каждый раз, когда мы генерируем новое состояние DFA под столбцами входного алфавита, мы должны снова применять шаг 4, в противном случае переходите к шагу 6.
Шаг 6 — Состояния, которые содержат любое из конечных состояний NDFA, являются конечными состояниями эквивалентного DFA.
пример
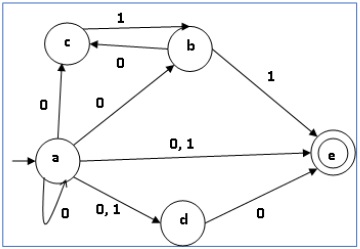
Давайте рассмотрим NDFA, показанный на рисунке ниже.
| Q | δ (д, 0) | δ (д, 1) |
|---|---|---|
| {А, б, в, д, е} | {Д, е} | |
| б | {C} | {Е} |
| с | ∅ | {Ь} |
| d | {Е} | ∅ |
| е | ∅ | ∅ |
Используя приведенный выше алгоритм, мы найдем его эквивалент DFA. Таблица состояний DFA показана ниже.
| Q | δ (д, 0) | δ (д, 1) |
|---|---|---|
| [А] | [А, б, в, д, е] | [D, е] |
| [А, б, в, д, е] | [А, б, в, д, е] | [Б, г, е] |
| [D, е] | [Е] | ∅ |
| [Б, г, е] | [С, е] | [Е] |
| [Е] | ∅ | ∅ |
| [с, е] | ∅ | [Ь] |
| [Ь] | [С] | [Е] |
| [С] | ∅ | [Ь] |
Диаграмма состояний DFA выглядит следующим образом —