Теория автоматов Введение

Термин «автоматы» происходит от греческого слова «αὐτόματα», что означает «самодействующий». Автомат (множественные числа автоматов) — это абстрактное самоходное вычислительное устройство, которое автоматически выполняет заданную последовательность операций.

Автомат с конечным числом состояний называется конечным автоматом (FA) или конечным автоматом (FSM).

Формальное определение конечного автомата

Автомат может быть представлен 5-кортежем (Q, ∑, δ, q ₀ , F), где —

• Q — конечное множество состояний.

• ∑ — это конечный набор символов, называемый алфавитом автомата.

• δ — функция перехода.

• q ₀ — начальное состояние, из которого обрабатывается любой вход (q ₀ ∈ Q).

• F — множество конечных состояний / состояний Q (F ⊆ Q).

Q — конечное множество состояний.

∑ — это конечный набор символов, называемый алфавитом автомата.

δ — функция перехода.

q ₀ — начальное состояние, из которого обрабатывается любой вход (q ₀ ∈ Q).

F — множество конечных состояний / состояний Q (F ⊆ Q).

Связанные термины

Алфавит

• Определение . Алфавит — это любой конечный набор символов.

• Пример — ∑ = {a, b, c, d} — набор алфавитов, где «a», «b», «c» и «d» — символы .

Определение . Алфавит — это любой конечный набор символов.

Пример — ∑ = {a, b, c, d} — набор алфавитов, где «a», «b», «c» и «d» — символы .

строка

• Определение — Строка — это конечная последовательность символов, взятая из ∑.

• Пример — ‘cabcad’ является допустимой строкой в ​​наборе алфавитов ∑ = {a, b, c, d}

Определение — Строка — это конечная последовательность символов, взятая из ∑.

Пример — ‘cabcad’ является допустимой строкой в ​​наборе алфавитов ∑ = {a, b, c, d}

Длина строки

• Определение — это количество символов, присутствующих в строке. (Обозначается | S | ).

• Примеры —

  • Если S = ​​’Cabcad’, | S | = 6

  • Если | S | = 0, это называется пустой строкой (Обозначается через λ или ε )

Определение — это количество символов, присутствующих в строке. (Обозначается | S | ).

Примеры —

Если S = ​​’Cabcad’, | S | = 6

Если | S | = 0, это называется пустой строкой (Обозначается через λ или ε )

Клини Стар

• Определение — звезда Клини, ∑ * , является унарным оператором на множестве символов или строк, ∑ , который дает бесконечный набор всех возможных строк всех возможных длин над ∑, включая λ .

• Представление — ∑ * = ∑ ₀ ∪ ∑ ₁ ∪ ∑ ₂ ∪ ……. где ∑ _p — множество всех возможных строк длины p.

• Пример — Если ∑ = {a, b}, ∑ * = {λ, a, b, aa, ab, ba, bb, ……… ..}

Определение — звезда Клини, ∑ * , является унарным оператором на множестве символов или строк, ∑ , который дает бесконечный набор всех возможных строк всех возможных длин над ∑, включая λ .

Представление — ∑ * = ∑ ₀ ∪ ∑ ₁ ∪ ∑ ₂ ∪ ……. где ∑ _p — множество всех возможных строк длины p.

Пример — Если ∑ = {a, b}, ∑ * = {λ, a, b, aa, ab, ba, bb, ……… ..}

Клини Закрытие / Плюс

• Определение — Множество ∑ ⁺ является бесконечным множеством всех возможных строк всех возможных длин над ∑, исключая λ.

• Представление — ∑ ⁺ = ∑ ₁ ∪ ∑ ₂ ∪ ∑ ₃ ∪ …….

  ∑ ⁺ = ∑ * — {λ}

• Пример — Если ∑ = {a, b}, ∑ ⁺ = {a, b, aa, ab, ba, bb, ……… ..}

Определение — Множество ∑ ⁺ является бесконечным множеством всех возможных строк всех возможных длин над ∑, исключая λ.

Представление — ∑ ⁺ = ∑ ₁ ∪ ∑ ₂ ∪ ∑ ₃ ∪ …….

∑ ⁺ = ∑ * — {λ}

Пример — Если ∑ = {a, b}, ∑ ⁺ = {a, b, aa, ab, ba, bb, ……… ..}

язык

• Определение — язык является подмножеством ∑ * для некоторого алфавита ∑. Это может быть конечным или бесконечным.

• Пример — если язык принимает все возможные строки длины 2 за ∑ = {a, b}, то L = {ab, aa, ba, bb}

Определение — язык является подмножеством ∑ * для некоторого алфавита ∑. Это может быть конечным или бесконечным.

Пример — если язык принимает все возможные строки длины 2 за ∑ = {a, b}, то L = {ab, aa, ba, bb}

Детерминированный конечный автомат

Конечный автомат можно разделить на два типа —

• Детерминированный конечный автомат (DFA)
• Недетерминированный конечный автомат (NDFA / NFA)

Детерминированный конечный автомат (DFA)

В DFA для каждого входного символа можно определить состояние, в которое машина перейдет. Следовательно, это называется Детерминированный Автомат . Поскольку оно имеет конечное число состояний, машина называется « Детерминированный конечный автомат» или « Детерминированный конечный автомат».

Формальное определение DFA

DFA может быть представлен 5-кортежем (Q, ∑, δ, q ₀ , F), где —

• Q — конечное множество состояний.

• ∑ — это конечный набор символов, называемый алфавитом.

• δ — функция перехода, где δ: Q × ∑ → Q

• q ₀ — начальное состояние, из которого обрабатывается любой вход (q ₀ ∈ Q).

• F — множество конечных состояний / состояний Q (F ⊆ Q).

Q — конечное множество состояний.

∑ — это конечный набор символов, называемый алфавитом.

δ — функция перехода, где δ: Q × ∑ → Q

q ₀ — начальное состояние, из которого обрабатывается любой вход (q ₀ ∈ Q).

F — множество конечных состояний / состояний Q (F ⊆ Q).

Графическое представление DFA

DFA представлен орграфами, которые называются диаграммой состояний .

• Вершины представляют состояния.
• Дуги, помеченные входным алфавитом, показывают переходы.
• Начальное состояние обозначается пустой единственной входящей дугой.
• Конечное состояние обозначено двойными кружками.

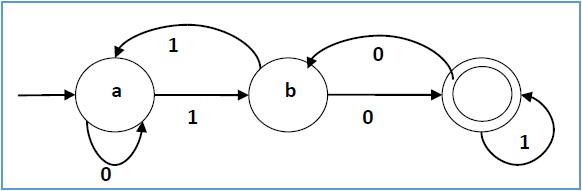
пример

Пусть детерминированный конечный автомат будет →

• Q = {a, b, c},
• ∑ = {0, 1},
• q ₀ = {а},
• F = {c} и

Функция перехода δ, как показано в следующей таблице —

Современное состояние	Следующее состояние для ввода 0	Следующее состояние для ввода 1
		б
б	с
с	б	с

Его графическое представление будет следующим:

Недетерминированный конечный автомат

В NDFA для определенного входного символа машина может перейти в любую комбинацию состояний в машине. Другими словами, точное состояние, в которое перемещается машина, не может быть определено. Следовательно, он называется недетерминированным автоматом . Поскольку оно имеет конечное число состояний, машина называется недетерминированным конечным автоматом или недетерминированным конечным автоматом .

Формальное определение NDFA

NDFA может быть представлен 5-кортежем (Q, ∑, δ, q ₀ , F), где —

• Q — конечное множество состояний.

• ∑ — это конечный набор символов, называемых алфавитами.

• δ — функция перехода, где δ: Q × ∑ → 2 ^Q

  (Здесь набор мощности Q (2 ^Q ) был взят, потому что в случае NDFA из состояния может произойти переход к любой комбинации состояний Q)

• q ₀ — начальное состояние, из которого обрабатывается любой вход (q ₀ ∈ Q).

• F — множество конечных состояний / состояний Q (F ⊆ Q).

Q — конечное множество состояний.

∑ — это конечный набор символов, называемых алфавитами.

δ — функция перехода, где δ: Q × ∑ → 2 ^Q

(Здесь набор мощности Q (2 ^Q ) был взят, потому что в случае NDFA из состояния может произойти переход к любой комбинации состояний Q)

q ₀ — начальное состояние, из которого обрабатывается любой вход (q ₀ ∈ Q).

F — множество конечных состояний / состояний Q (F ⊆ Q).

Графическое представление NDFA: (так же, как DFA)

NDFA представлен орграфами, которые называются диаграммой состояний.

• Вершины представляют состояния.
• Дуги, помеченные входным алфавитом, показывают переходы.
• Начальное состояние обозначается пустой единственной входящей дугой.
• Конечное состояние обозначено двойными кружками.

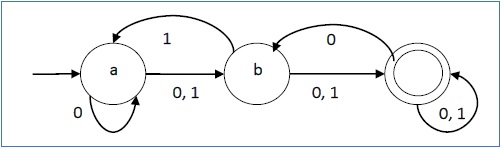
пример

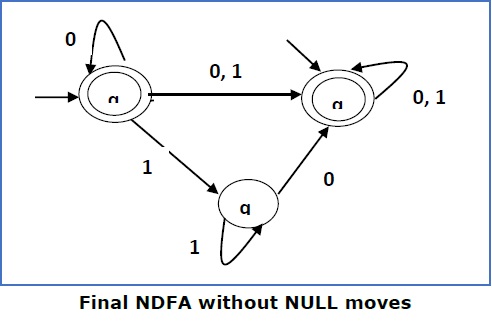
Пусть недетерминированный конечный автомат будет →

• Q = {a, b, c}
• ∑ = {0, 1}
• q ₀ = {а}
• F = {c}

Функция перехода δ, как показано ниже —

Современное состояние	Следующее состояние для ввода 0	Следующее состояние для ввода 1
	а, б	б
б	с	а, с
с	До нашей эры	с

Его графическое представление будет следующим:

ДФА против НДФА

В следующей таблице перечислены различия между DFA и NDFA.

DFA	NDFA
Переход из состояния в одно конкретное следующее состояние для каждого входного символа. Следовательно это называется детерминированным .	Переход из состояния может быть в несколько следующих состояний для каждого входного символа. Следовательно это называется недетерминированным .
Пустые строковые переходы не видны в DFA.	NDFA разрешает переходы пустой строки.
Отклонение разрешено в DFA	В NDFA откат не всегда возможен.
Требуется больше места.	Требует меньше места.
DFA принимает строку, если она переходит в конечное состояние.	NDFA принимает строку, если хотя бы один из всех возможных переходов заканчивается в конечном состоянии.

Акцепторы, классификаторы и преобразователи

Акцептор (Распознаватель)

Автомат, который вычисляет булеву функцию, называется акцептором . Все состояния акцептора либо принимают, либо отклоняют введенные ему входные данные.

классификатор

Классификатор имеет более двух конечных состояний и выдает один выход при его завершении.

преобразователь

Автомат, который производит выходные данные на основе текущего входа и / или предыдущего состояния, называется преобразователем . Преобразователи могут быть двух типов —

• Мили Машина — выход зависит как от текущего состояния и текущего ввода.

• Moore Machine — Выход зависит только от текущего состояния.

Мили Машина — выход зависит как от текущего состояния и текущего ввода.

Moore Machine — Выход зависит только от текущего состояния.

Приемлемость DFA и NDFA

DFA / NDFA принимает строку, если DFA / NDFA, начиная с начального состояния, заканчивается после полного чтения строки в состоянии принятия (любом из конечных состояний).

Строка S принимается DFA / NDFA (Q, ∑, δ, q ₀ , F), если

δ * (q ₀ , S) ∈ F

Язык L принятый DFA / NDFA:

{S | S ∈ ∑ * и δ * (q ₀ , S) ∈ F}

Строка S ′ не принимается DFA / NDFA (Q, ∑, δ, q ₀ , F), если

δ * (q ₀ , S ′) ∉ F

Язык L ′ не принят DFA / NDFA (дополнение к принятому языку L)

{S | S ∈ ∑ * и δ * (q ₀ , S) ∉ F}

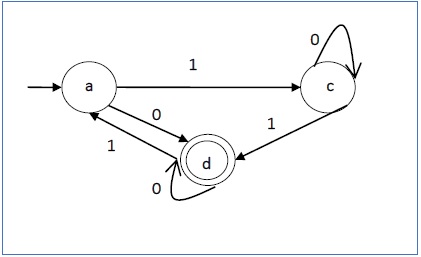
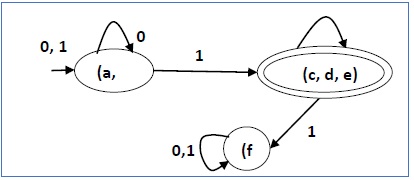
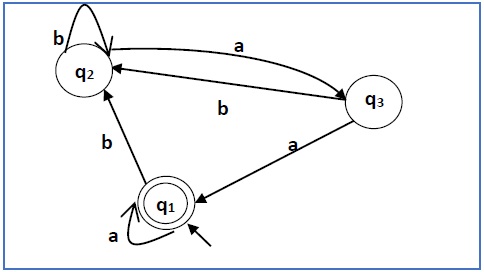
пример

Давайте рассмотрим DFA, показанный на рисунке 1.3. Из DFA, приемлемые строки могут быть получены.

Строки, принятые вышеуказанным DFA: {0, 00, 11, 010, 101, ………..}

Строки, не принятые вышеуказанным DFA: {1, 011, 111, ……..}

Конвертация NDFA в DFA

Постановка задачи

Пусть X = (Q _x , ∑, δ _x , q ₀ , F _x ) NDFA, который принимает язык L (X). Мы должны спроектировать эквивалентный DFA Y = (Q _y , ∑, δ _y , q ₀ , F _y ) такой, что L (Y) = L (X) . Следующая процедура преобразует NDFA в эквивалентный DFA —

Алгоритм

Вход — NDFA

Выход — эквивалент DFA

Шаг 1 — Создать таблицу состояний из заданного NDFA.

Шаг 2 — Создайте пустую таблицу состояний под возможными входными алфавитами для эквивалентного DFA.

Шаг 3 — Отметьте начальное состояние DFA как q0 (то же самое, что и NDFA).

Шаг 4 — Узнайте комбинацию состояний {Q ₀ , Q ₁ , …, Q _n } для каждого возможного входного алфавита.

Шаг 5 — Каждый раз, когда мы генерируем новое состояние DFA под столбцами входного алфавита, мы должны снова применять шаг 4, в противном случае переходите к шагу 6.

Шаг 6 — Состояния, которые содержат любое из конечных состояний NDFA, являются конечными состояниями эквивалентного DFA.

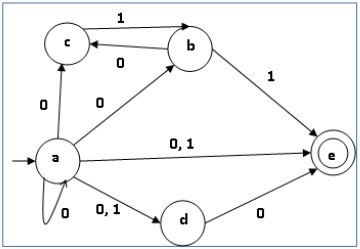
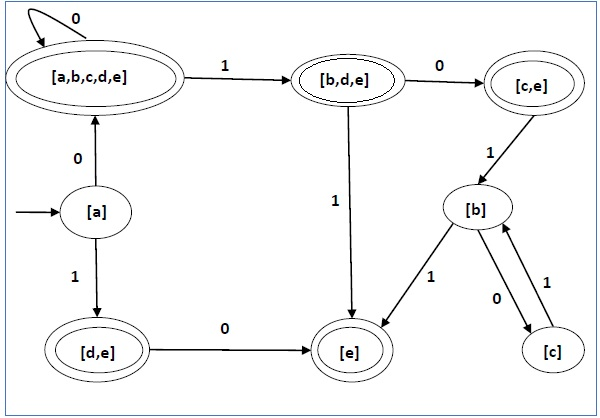
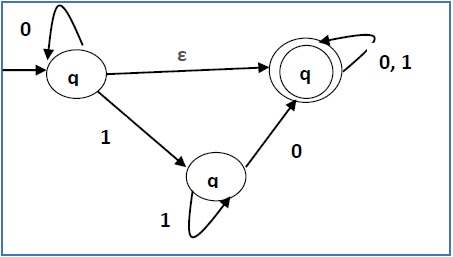
пример

Давайте рассмотрим NDFA, показанный на рисунке ниже.

Q	δ (д, 0)	δ (д, 1)
	{А, б, в, д, е}	{Д, е}
б	{C}	{Е}
с	∅	{Ь}
d	{Е}	∅
е	∅	∅

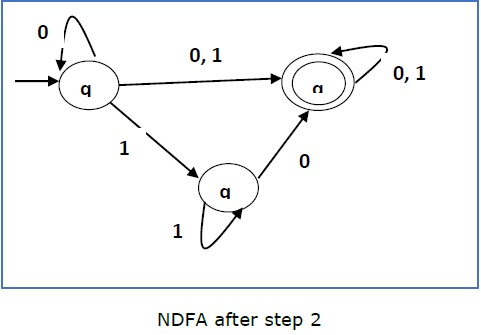
Используя приведенный выше алгоритм, мы найдем его эквивалент DFA. Таблица состояний DFA показана ниже.

Q	δ (д, 0)	δ (д, 1)
[А]	[А, б, в, д, е]	[D, е]
[А, б, в, д, е]	[А, б, в, д, е]	[Б, г, е]
[D, е]	[Е]	∅
[Б, г, е]	[С, е]	[Е]
[Е]	∅	∅
[с, е]	∅	[Ь]
[Ь]	[С]	[Е]
[С]	∅	[Ь]

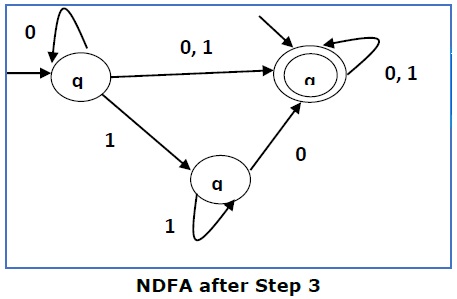
Диаграмма состояний DFA выглядит следующим образом —

DFA Минимизация

Минимизация DFA с использованием теоремы Мифилла-Нерода

Алгоритм

Вход — DFA

Вывод — минимизированный DFA

Шаг 1 — Нарисуйте таблицу для всех пар состояний (Q _i , Q _j ), не обязательно связанных напрямую [Все изначально не отмечены]

Шаг 2 — Рассмотрим каждую пару состояний (Q _i , Q _j ) в DFA, где Q _i ∈ F и Q _j ∉ F, или наоборот, и отметьте их. [Здесь F — множество конечных состояний]

Шаг 3 — Повторяйте этот шаг, пока мы больше не сможем помечать состояния —

Если есть немаркированная пара (Q _i , Q _j ), отметьте ее, если пара {δ (Q _i , A), δ (Q _i , A)} отмечена для некоторого входного алфавита.

Шаг 4 — Объедините все непомеченные пары (Q _i , Q _j ) и сделайте их единым состоянием в сокращенном DFA.

пример

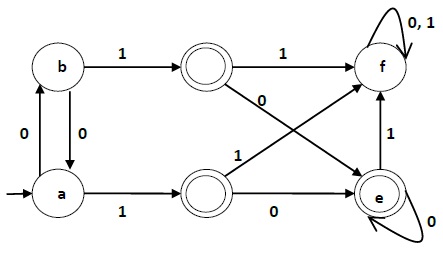
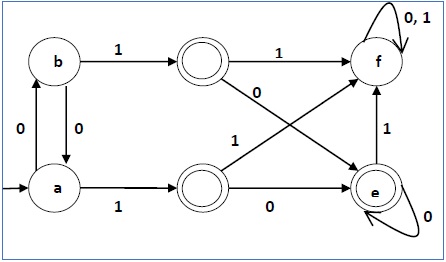
Давайте используем алгоритм 2, чтобы минимизировать DFA, показанный ниже.

Шаг 1 — Нарисуем таблицу для всех пар состояний.

		б	с	d	е	е
б
с
d
е
е

Шаг 2 — Отметим пары состояний.

		б	с	d	е	е
б
с	✔	✔
d	✔	✔
е	✔	✔
е			✔	✔	✔

Шаг 3 — Мы попытаемся пометить пары состояний, отмеченные зеленым цветом, транзитивно. Если мы введем 1 в состояние «a» и «f», он перейдет в состояние «c» и «f» соответственно. (c, f) уже отмечен, поэтому мы будем отмечать пару (a, f). Теперь мы вводим 1 в состояние «b» и «f»; он перейдет в состояние «d» и «f» соответственно. (d, f) уже отмечен, поэтому мы будем отмечать пару (b, f).

		б	с	d	е	е
б
с	✔	✔
d	✔	✔
е	✔	✔
е	✔	✔	✔	✔	✔

После шага 3 у нас есть комбинации состояний {a, b} {c, d} {c, e} {d, e}, которые не отмечены.

Мы можем рекомбинировать {c, d} {c, e} {d, e} в {c, d, e}

Следовательно, мы получили два комбинированных состояния как — {a, b} и {c, d, e}

Таким образом, окончательный свернутый DFA будет содержать три состояния {f}, {a, b} и {c, d, e}

Минимизация DFA с использованием теоремы об эквивалентности

Если X и Y — два состояния в DFA, мы можем объединить эти два состояния в {X, Y}, если они не различимы. Два состояния различимы, если есть хотя бы одна строка S, так что одно из δ (X, S) и δ (Y, S) принимает, а другое не принимает. Следовательно, DFA минимален тогда и только тогда, когда все состояния различимы.

Алгоритм 3

Шаг 1 — Все состояния Q разделены на два раздела — конечные состояния и неконечные состояния и обозначены P ₀ . Все состояния в разделе имеют 0- ^й эквивалент. Возьмите счетчик k и инициализируйте его 0.

Шаг 2. Увеличьте k на 1. Для каждого разбиения в P _k разделите состояния в P _k на два разбиения, если они различимы по k. Два состояния в этом разделе X и Y являются k-различимыми, если существует вход S такой, что δ (X, S) и δ (Y, S) являются (k-1) -различимыми.

Шаг 3 — Если P _k ≠ P _k-1 , повторите шаг 2, в противном случае перейдите к шагу 4.

Шаг 4 — Объедините k- ^е эквивалентные наборы и сделайте их новыми состояниями сокращенного DFA.

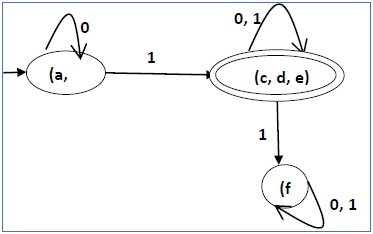
пример

Давайте рассмотрим следующий DFA —

Q	δ (д, 0)	δ (д, 1)
	б	с
б		d
с	е	е
d	е	е
е	е	е
е	е	е

Давайте применим вышеупомянутый алгоритм к вышеупомянутому DFA —

• P ₀ = {(c, d, e), (a, b, f)}
• P ₁ = {(c, d, e), (a, b), (f)}
• P ₂ = {(c, d, e), (a, b), (f)}

Следовательно, P ₁ = P ₂ .

В сокращенном DFA есть три состояния. Уменьшенный DFA выглядит следующим образом —

Q	δ (д, 0)	δ (д, 1)
(а, б)	(а, б)	(В, г, д)
(В, г, д)	(В, г, д)	(Е)
(Е)	(Е)	(Е)

Мур и Мили Машины

Конечные автоматы могут иметь выходные данные, соответствующие каждому переходу. Существует два типа конечных автоматов, которые генерируют вывод:

• Мили Машина
• Мур машина

Мили Машина

Мили-машина — это FSM, выход которого зависит от текущего состояния, а также от текущего ввода.

Он может быть описан набором 6 (Q, ∑, O, δ, X, q ₀ ), где —

• Q — конечное множество состояний.

• ∑ — это конечный набор символов, называемый входным алфавитом.

• O — это конечный набор символов, называемый выходным алфавитом.

• δ — функция входного перехода, где δ: Q × ∑ → Q

• X — функция выходного перехода, где X: Q × ∑ → O

• q ₀ — начальное состояние, из которого обрабатывается любой вход (q ₀ ∈ Q).

Q — конечное множество состояний.

∑ — это конечный набор символов, называемый входным алфавитом.

O — это конечный набор символов, называемый выходным алфавитом.

δ — функция входного перехода, где δ: Q × ∑ → Q

X — функция выходного перехода, где X: Q × ∑ → O

q ₀ — начальное состояние, из которого обрабатывается любой вход (q ₀ ∈ Q).

Таблица состояний Мили-машины показана ниже —

Современное состояние	Следующее состояние
	вход = 0		вход = 1
	государственный	Выход	государственный	Выход
→ а	б	х 1	с	х 1
б	б	х 2	d	х 3
с	d	х 3	с	х 1
d	d	х 3	d	х 2

Диаграмма состояния вышеупомянутого Мили Машины —

Мур машина

Машина Мура является автоматом, выход которого зависит только от текущего состояния.

Машина Мура может быть описана набором из 6 (Q, ∑, O, δ, X, q ₀ ), где —

• Q — конечное множество состояний.

• ∑ — это конечный набор символов, называемый входным алфавитом.

• O — это конечный набор символов, называемый выходным алфавитом.

• δ — функция входного перехода, где δ: Q × ∑ → Q

• X — функция выходного перехода, где X: Q → O

• q ₀ — начальное состояние, из которого обрабатывается любой вход (q ₀ ∈ Q).

Q — конечное множество состояний.

∑ — это конечный набор символов, называемый входным алфавитом.

O — это конечный набор символов, называемый выходным алфавитом.

δ — функция входного перехода, где δ: Q × ∑ → Q

X — функция выходного перехода, где X: Q → O

q ₀ — начальное состояние, из которого обрабатывается любой вход (q ₀ ∈ Q).

Таблица состояний машины Мура показана ниже —

Современное состояние	Следующее состояние		Выход
	Вход = 0	Вход = 1
→ а	б	с	х 2
б	б	d	х 1
с	с	d	х 2
d	d	d	х 3

Диаграмма состояний вышеуказанной машины Мура —

Мили машина против Мура машины

В следующей таблице выделены точки, которые отличают машину Мили от машины Мура.

Мили Машина	Мур машина
Выход зависит как от текущего состояния, так и от текущего ввода	Выход зависит только от текущего состояния.
Как правило, в нем меньше состояний, чем в Moore Machine.	Как правило, он имеет больше состояний, чем Мили Машина.
Значение функции выхода является функцией переходов и изменений, когда логика ввода в текущем состоянии выполнена.	Значение выходной функции является функцией текущего состояния и изменений по краям часов, когда бы ни происходили изменения состояния.
Мили машины реагируют быстрее на входы. Они обычно реагируют в одном и том же тактовом цикле.	В машинах Мура для декодирования выходов требуется больше логики, что приводит к большим задержкам в цепи. Они обычно реагируют на один такт позже.

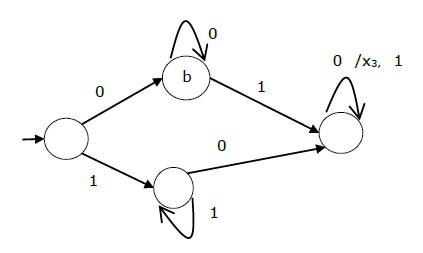
Мур машина в Мили машина

Алгоритм 4

Вход — машина Мура

Выход — Мили Машина

Шаг 1 — Возьмите пустой формат таблицы переходов Mealy Machine.

Шаг 2 — Скопируйте все переходные состояния машины Мура в этот формат таблицы.

Шаг 3 — Проверьте текущие состояния и их соответствующие выходы в таблице состояний машины Мура; если для состояния Q _i вывод равен m, скопируйте его в выходные столбцы таблицы состояний Mealy Machine везде, где Q _i появляется в следующем состоянии.

пример

Давайте рассмотрим следующую машину Мура —

Современное состояние	Следующее состояние		Выход
	а = 0	а = 1
→ а	d	б	1
б		d	0
с	с	с	0
d	б		1

Теперь мы применяем алгоритм 4, чтобы преобразовать его в Mealy Machine.

Шаг 1 и 2 —

Современное состояние	Следующее состояние
	а = 0		а = 1
	государственный	Выход	государственный	Выход
→ а	d		б
б			d
с	с		с
d	б

Шаг 3 —

Современное состояние	Следующее состояние
	а = 0		а = 1
	государственный	Выход	государственный	Выход
=> а	d	1	б	0
б		1	d	1
с	с	0	с	0
d	б	0		1

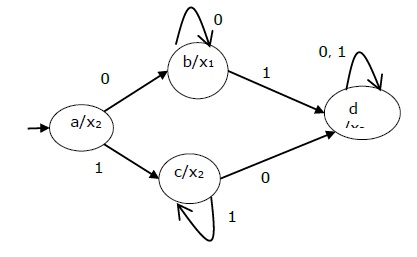
Мили машина для машины Мура

Алгоритм 5

Ввод — Мили Машина

Выход — машина Мура

Шаг 1 — Рассчитайте количество различных выходов для каждого состояния (Q _i ), которые доступны в таблице состояний машины Мили.

Шаг 2 — Если все выходы Qi одинаковы, скопируйте состояние Q _i . Если он имеет n различных выходов, разбейте Q _i на n состояний как Q, где n = 0, 1, 2 …….

Шаг 3 — Если выходные данные начального состояния равны 1, вставьте новое начальное состояние в начале, которое дает 0 выходных данных.

пример

Давайте рассмотрим следующую машину Мили —

Современное состояние	Следующее состояние
	а = 0		а = 1
	Следующее состояние	Выход	Следующее состояние	Выход
→ а	d	0	б	1
б		1	d	0
с	с	1	с	0
d	б	0		1

Здесь состояния «a» и «d» дают только 1 и 0 выходных сигналов соответственно, поэтому мы сохраняем состояния «a» и «d». Но состояния ‘b’ и ‘c’ дают разные результаты (1 и 0). Итак, мы разделим b на b ₀ , b ₁ и c на c ₀ , c ₁ .

Современное состояние	Следующее состояние		Выход
	а = 0	а = 1
→ а	d	б 1	1
б 0		d	0
б 1		d	1
с 0	с 1	C 0	0
с 1	с 1	C 0	1
d	б 0		0

Введение в грамматику

В литературном смысле этого термина грамматики обозначают синтаксические правила общения на естественных языках. Лингвистика пыталась определить грамматику с момента появления естественных языков, таких как английский, санскрит, мандарин и т. Д.

Теория формальных языков находит широкое применение в области компьютерных наук. Ноам Хомский дал математическую модель грамматики в 1956 году, которая эффективна для написания компьютерных языков.

грамматика

Грамматика G может быть формально записана в виде 4-х кортежей (N, T, S, P), где —

• N или V _N — это набор переменных или нетерминальных символов.

• T или ∑ — это набор символов терминала.

• S — это специальная переменная, называемая символом начала, S ∈ N

• P — Правила производства для терминалов и нетерминалов. Производственное правило имеет вид α → β, где α и β — строки на V _N ∪ ∑, и хотя бы один символ α принадлежит V _N.

N или V _N — это набор переменных или нетерминальных символов.

T или ∑ — это набор символов терминала.

S — это специальная переменная, называемая символом начала, S ∈ N

P — Правила производства для терминалов и нетерминалов. Производственное правило имеет вид α → β, где α и β — строки на V _N ∪ ∑, и хотя бы один символ α принадлежит V _N.

пример

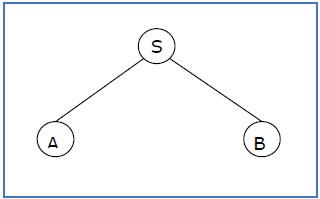
Грамматика G1 —

({S, A, B}, {a, b}, S, {S → AB, A → a, B → b})

Вот,

• S, A и B — нетерминальные символы;

• a и b являются терминальными символами

• S — начальный символ, S ∈ N

• Производства, P: S → AB, A → a, B → b

S, A и B — нетерминальные символы;

a и b являются терминальными символами

S — начальный символ, S ∈ N

Производства, P: S → AB, A → a, B → b

пример

Грамматика G2 —

(({S, A}, {a, b}, S, {S → aAb, aA → aaAb, A → ε})

Вот,

• S и A — нетерминальные символы.

• a и b являются терминальными символами.

• ε — пустая строка.

• S — начальный символ, S ∈ N

• Производство P: S → aAb, aA → aaAb, A → ε

S и A — нетерминальные символы.

a и b являются терминальными символами.

ε — пустая строка.

S — начальный символ, S ∈ N

Производство P: S → aAb, aA → aaAb, A → ε

Выводы из грамматики

Строки могут быть получены из других строк с использованием произведений в грамматике. Если грамматика G имеет произведение α → β , мы можем сказать, что x α y выводит x β y в G. Этот вывод записывается как —

x α y ⇒ G x β y

пример

Давайте рассмотрим грамматику —

G2 = ({S, A}, {a, b}, S, {S → aAb, aA → aaAb, A → ε})

Некоторые из строк, которые могут быть получены:

S ⇒ aA b с использованием продукции S → aAb

⇒ a aA bb с использованием продукции aA → aAb

⇒ aaa A bbb с использованием производства aA → aAb

⇒ aaabbb с использованием продукции A → ε

Язык, созданный грамматикой

Говорят, что набор всех строк, которые могут быть получены из грамматики, является языком, сгенерированным из этой грамматики. Язык, генерируемый грамматикой G, представляет собой подмножество, формально определяемое как

L (G) = {W | W ∈ ∑ *, S ⇒ G W }

Если L (G1) = L (G2) , грамматика G1 эквивалентна грамматике G2 .

пример

Если есть грамматика

G: N = {S, A, B} T = {a, b} P = {S → AB, A → a, B → b}

Здесь S производит AB , и мы можем заменить A на a , а B на b . Здесь единственной принятой строкой является ab , т.е.

L (G) = {ab}

пример

Предположим, у нас есть следующая грамматика —

G: N = {S, A, B} T = {a, b} P = {S → AB, A → aA | a, B → bB | b}

Язык, генерируемый этой грамматикой —

L (G) = {ab, a ² b, ab ² , a ² b ² , ………}

= {a ^m b ⁿ | m ≥ 1 и n ≥ 1}

Построение грамматики, порождающей язык

Мы рассмотрим некоторые языки и преобразуем их в грамматику G, которая производит эти языки.

пример

Задача — Предположим, что L (G) = {a ^m b ⁿ | m ≥ 0 и n> 0}. Мы должны выяснить грамматику G, которая производит L (G) .

Решение

Поскольку L (G) = {a ^m b ⁿ | m ≥ 0 и n> 0}

набор принятых строк может быть переписан как —

L (G) = {b, ab, bb, aab, abb, …….}

Здесь начальный символ должен содержать хотя бы одну букву «b», которой предшествует любое число «a», включая ноль.

Чтобы принять набор строк {b, ab, bb, aab, abb, …….}, Мы взяли продукцию —

S → aS, S → B, B → b и B → bB

S → B → b (принято)

S → B → bB → bb (принято)

S → aS → aB → ab (принято)

S → aS → aaS → aaB → aab (принято)

S → aS → aB → abB → abb (принято)

Таким образом, мы можем доказать, что каждая отдельная строка в L (G) принята языком, сгенерированным производственным набором.

Отсюда и грамматика

G: ({S, A, B}, {a, b}, S, {S → aS | B, B → b | bB})

пример

Задача — Предположим, что L (G) = {a ^m b ⁿ | m> 0 и n ≥ 0}. Мы должны выяснить грамматику G, которая производит L (G).

Решение —

Поскольку L (G) = {a ^m b ⁿ | m> 0 и n ≥ 0}, набор принятых строк можно переписать как —

L (G) = {a, aa, ab, aaa, aab, abb, …….}

Здесь начальный символ должен содержать хотя бы одну букву «a», за которой следует любое число «b», включая ноль.

Чтобы принять набор строк {a, aa, ab, aaa, aab, abb, …….}, Мы взяли произведения:

S → aA, A → aA, A → B, B → bB, B → λ

S → aA → aB → aλ → a (принято)

S → aA → aaA → aaB → aaλ → aa (принято)

S → aA → aB → abB → abλ → ab (принято)

S → aA → aaA → aaaA → aaaB → aaaλ → aaa (принято)

S → aA → aaA → aaB → aabB → aabλ → aab (принято)

S → aA → aB → abB → abbB → abbλ → abb (принято)

Таким образом, мы можем доказать, что каждая отдельная строка в L (G) принята языком, сгенерированным производственным набором.

Отсюда и грамматика

G: ({S, A, B}, {a, b}, S, {S → aA, A → aA | B, B → λ | bB})

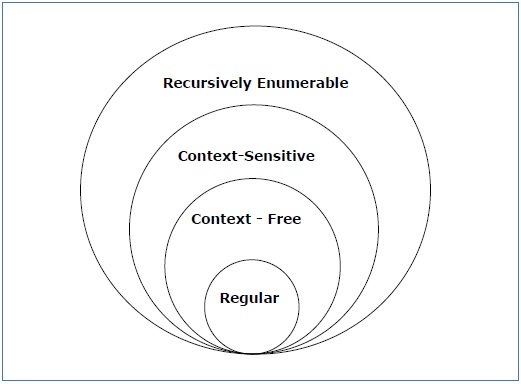
Хомская классификация грамматик

Согласно Ноаму Хомоски, существует четыре типа грамматик — Тип 0, Тип 1, Тип 2 и Тип 3. В следующей таблице показано, как они отличаются друг от друга —

Тип грамматики	Грамматика принята	Язык принят	Автомат
Тип 0	Неограниченная грамматика	Рекурсивно перечислимый язык	Машина Тьюринга
Тип 1	Контекстно-зависимая грамматика	Контекстно-зависимый язык	Линейно-ограниченный автомат
Тип 2	Контекстная грамматика	Контекстно-свободный язык	Pushdown автомат
Тип 3	Обычная грамматика	Обычный язык	Конечный автомат

Посмотрите на следующую иллюстрацию. Он показывает объем каждого типа грамматики —

Тип — 3 грамматики

Грамматики типа 3 генерируют обычные языки. Грамматики типа 3 должны иметь один нетерминал с левой стороны и правую сторону, состоящую из одного терминала или одного терминала, за которым следует один нетерминал.

Произведения должны быть в форме X → a или X → aY

где X, Y ∈ N (нетерминал)

и a ∈ T (терминал)

Правило S → ε допустимо, если S не появляется справа от какого-либо правила.

пример

X → ε 
X → a | aY
Y → b 

Тип — 2 грамматики

Грамматики типа 2 генерируют языки без контекста.

Произведения должны быть в форме A → γ

где A ∈ N (нетерминал)

и γ ∈ (T ∪ N) * (строка терминалов и нетерминалов).

Эти языки, генерируемые этими грамматиками, распознаются недетерминированным автоматом.

пример

S → X a 
X → a 
X → aX 
X → abc 
X → ε

Тип — 1 грамматика

Грамматики типа 1 генерируют контекстно-зависимые языки. Продукция должна быть в форме

α A β → α γ β

где A ∈ N (нетерминал)

и α, β, γ ∈ (T ∪ N) * (строки терминалов и нетерминалов)

Строки α и β могут быть пустыми, но γ должна быть непустой.

Правило S → ε допустимо, если S не появляется справа от какого-либо правила. Языки, генерируемые этими грамматиками, распознаются линейным ограниченным автоматом.

пример

AB → AbBc 
A → bcA 
B → b 

Тип — 0 Грамматика

Грамматики типа 0 генерируют рекурсивно перечислимые языки. Производства не имеют ограничений. Это грамматика любой фазовой структуры, включая все формальные грамматики.

Они генерируют языки, которые распознаются машиной Тьюринга.

Произведения могут быть в форме α → β, где α — строка терминалов и нетерминалов, по крайней мере, с одним нетерминалом, и α не может быть нулевым. β — цепочка терминалов и нетерминалов.

пример

S → ACaB 
Bc → acB 
CB → DB 
aD → Db 

Регулярные выражения

Регулярное выражение может быть рекурсивно определено следующим образом:

• ε является регулярным выражением, обозначающим язык, содержащий пустую строку. (L (ε) = {ε})

• φ является регулярным выражением, обозначающим пустой язык. (L (φ) = {})

• x — это регулярное выражение, где L = {x}

• Если X является регулярным выражением, обозначающим язык L (X), а Y является регулярным выражением, обозначающим язык L (Y) , то

  • X + Y является регулярным выражением, соответствующим языку L (X) ∪ L (Y), где L (X + Y) = L (X) ∪ L (Y) .

  • ИКС . Y является регулярным выражением, соответствующим языку L (X). L (Y) где L (XY) = L (X). L (Y)

  • R * является регулярным выражением, соответствующим языку L (R *), где L (R *) = (L (R)) *

• Если мы применяем какое-либо из правил несколько раз от 1 до 5, это регулярные выражения.

ε является регулярным выражением, обозначающим язык, содержащий пустую строку. (L (ε) = {ε})

φ является регулярным выражением, обозначающим пустой язык. (L (φ) = {})

x — это регулярное выражение, где L = {x}

Если X является регулярным выражением, обозначающим язык L (X), а Y является регулярным выражением, обозначающим язык L (Y) , то

X + Y является регулярным выражением, соответствующим языку L (X) ∪ L (Y), где L (X + Y) = L (X) ∪ L (Y) .

ИКС . Y является регулярным выражением, соответствующим языку L (X). L (Y) где L (XY) = L (X). L (Y)

R * является регулярным выражением, соответствующим языку L (R *), где L (R *) = (L (R)) *

Если мы применяем какое-либо из правил несколько раз от 1 до 5, это регулярные выражения.

Некоторые примеры RE

Регулярные выражения	Обычный набор
(0 + 10 *)	L = {0, 1, 10, 100, 1000, 10000,…}
(0 * 10 *)	L = {1, 01, 10, 010, 0010,…}
(0 + ε) (1 + ε)	L = {ε, 0, 1, 01}
(А + б) *	Набор строк a и b любой длины, включая нулевую строку. Итак, L = {ε, a, b, aa, ab, bb, ba, aaa …….}
(А + б) * АВВ	Множество строк a и b, заканчивающихся строкой abb. Итак, L = {abb, aabb, babb, aaabb, ababb, ………… ..}
(11) *	Набор, состоящий из четного числа 1, включая пустую строку, поэтому L = {ε, 11, 1111, 111111, ……….}
(Аа) * (бб) * б	Набор строк, состоящий из четного числа a, за которым следует нечетное число b, поэтому L = {b, aab, aabbb, aabbbbb, aaaab, aaaabbb, ………… ..}
(aa + ab + ba + bb) *	Строки a и b одинаковой длины можно получить путем объединения любой комбинации строк aa, ab, ba и bb, включая ноль, поэтому L = {aa, ab, ba, bb, aaab, aaba, ………… .. }

Регулярные наборы

Любой набор, представляющий значение регулярного выражения, называется регулярным набором.

Свойства регулярных множеств

Свойство 1 . Объединение двух регулярных множеств является регулярным.

Доказательство —

Давайте возьмем два регулярных выражения

RE ₁ = a (aa) * и RE ₂ = (aa) *

Итак, L ₁ = {a, aaa, aaaaa, …..} (строки нечетной длины, исключая Null)

и L ₂ = {ε, aa, aaaa, aaaaaa, …….} (строки четной длины, включая ноль)

L ₁ ∪ L ₂ = {ε, a, aa, aaa, aaaa, aaaaa, aaaaaa, …….}

(Строки всех возможных длин, включая Null)

RE (L ₁ ∪ L ₂ ) = a * (что само является регулярным выражением)

Следовательно, доказано.

Свойство 2. Пересечение двух регулярных множеств регулярно.

Доказательство —

Давайте возьмем два регулярных выражения

RE ₁ = a (a *) и RE ₂ = (aa) *

Итак, L ₁ = {a, aa, aaa, aaaa, ….} (строки любой возможной длины, кроме Null)

L ₂ = {ε, aa, aaaa, aaaaaa, …….} (строки четной длины, включая ноль)

L ₁ ∩ L ₂ = {aa, aaaa, aaaaaa, …….} (строки четной длины, исключая Null)

RE (L ₁ ∩ L ₂ ) = aa (aa) *, что само является регулярным выражением.

Следовательно, доказано.

Свойство 3. Дополнение регулярного множества регулярно.

Доказательство —

Давайте возьмем регулярное выражение —

RE = (аа) *

Итак, L = {ε, aa, aaaa, aaaaaa, …….} (строки четной длины, включая ноль)

Дополнением к L являются все строки, которых нет в L.

Итак, L ‘= {a, aaa, aaaaa, …..} (строки нечетной длины, исключая Null)

RE (L ‘) = a (aa) *, которая сама является регулярным выражением.

Следовательно, доказано.

Свойство 4. Разница двух регулярных множеств регулярна.

Доказательство —

Давайте возьмем два регулярных выражения —

RE ₁ = a (a *) и RE ₂ = (aa) *

Итак, L ₁ = {a, aa, aaa, aaaa, ….} (строки любой возможной длины, кроме Null)

L ₂ = {ε, aa, aaaa, aaaaaa, …….} (строки четной длины, включая ноль)

L ₁ — L ₂ = {а, ааа, ааааа, ааааааа, ….}

(Строки всех нечетных длин, кроме Null)

RE (L ₁ — L ₂ ) = a (aa) *, что является регулярным выражением.

Следовательно, доказано.

Свойство 5. Обращение регулярного множества регулярно.

Доказательство —

Мы должны доказать, что L ^R также регулярно, если L регулярное множество.

Пусть L = {01, 10, 11, 10}

RE (L) = 01 + 10 + 11 + 10

L ^R = {10, 01, 11, 01}

RE (L ^R ) = 01 + 10 + 11 + 10, что регулярно

Следовательно, доказано.

Свойство 6. Закрытие регулярного множества регулярно.

Доказательство —

Если L = {a, aaa, aaaaa, …….} (строки нечетной длины, исключая Null)

то есть RE (L) = a (aa) *

L * = {a, aa, aaa, aaaa, aaaaa, ……………} (строки любой длины, кроме Null)

RE (L *) = a (a) *

Следовательно, доказано.

Свойство 7. Конкатенация двух регулярных множеств регулярна.

Доказательство —

Пусть RE ₁ = (0 + 1) * 0 и RE ₂ = 01 (0 + 1) *

Здесь L ₁ = {0, 00, 10, 000, 010, ……} (набор строк, заканчивающихся на 0)

и L ₂ = {01, 010,011, …..} (набор строк, начинающийся с 01)

Тогда L ₁ L ₂ = {001,0010,0011,0001,00010,00011,1001,10010, ………….}

Набор строк, содержащих 001 в качестве подстроки, которая может быть представлена ​​RE — (0 + 1) * 001 (0 + 1) *

Следовательно, доказано.

Тождества, связанные с регулярными выражениями

Учитывая R, P, L, Q как регулярные выражения, справедливы следующие тождества:

• ∅ * = ε
• ε * = ε
• RR * = R * R
• R * R * = R *
• (R *) * = R *
• RR * = R * R
• (PQ) * P = P (QP) *
• (a + b) * = (a * b *) * = (a * + b *) * = (a + b *) * = a * (ba *) *
• R + ∅ = ∅ + R = R (тождество для объединения)
• R ε = ε R = R (тождество для объединения)
• ∅ L = L ∅ = ∅ (Аннулятор для конкатенации)
• R + R = R (закон Идемпотента)
• L (M + N) = LM + LN (левый дистрибутивный закон)
• (M + N) L = ML + NL (Право дистрибутивного права)
• ε + RR * = ε + R * R = R *

Теорема Ардена

Чтобы найти регулярное выражение конечного автомата, мы используем теорему Ардена вместе со свойствами регулярных выражений.

Заявление —

Пусть P и Q два регулярных выражения.

Если P не содержит нулевую строку, то R = Q + RP имеет единственное решение, которое R = QP *

Доказательство —

R = Q + (Q + RP) P [После помещения значения R = Q + RP]

= Q + QP + RPP

Когда мы снова и снова ставим значение R рекурсивно, мы получаем следующее уравнение:

R = Q + QP + QP ² + QP ³ … ..

R = Q (ε + P + P ² + P ³ +….)

R = QP * [Как P * представляет (ε + P + P2 + P3 +….)]

Следовательно, доказано.

Предположения для применения теоремы Ардена

• Диаграмма переходов не должна иметь переходов NULL
• Должно быть только одно начальное состояние

метод

Шаг 1 — Создайте уравнения в виде следующей формы для всех состояний DFA, имеющих n состояний с начальным состоянием q ₁ .

q ₁ = q ₁ R ₁₁ + q ₂ R ₂₁ +… + q _n R _n1 + ε

q ₂ = q ₁ R ₁₂ + q ₂ R ₂₂ +… + q _n R _n2

…………………………

…………………………

…………………………

…………………………

q _n = q ₁ R _1n + q ₂ R _2n +… + q _n R _nn

R _ij представляет множество меток ребер от q _i до q _j , если такого ребра не существует, то R _ij = ∅

Шаг 2 — Решите эти уравнения, чтобы получить уравнение для конечного состояния в терминах R _ij

проблема

Построить регулярное выражение, соответствующее автоматам, приведенным ниже —

Решение —

Здесь начальное состояние и конечное состояние q ₁ .

Уравнения для трех состояний q1, q2 и q3 следующие:

q ₁ = q ₁ a + q ₃ a + ε (перемещение ε происходит потому, что q1 является начальным состоянием 0

q ₂ = q ₁ b + q ₂ b + q ₃ b

q ₃ = q ₂ a

Теперь мы будем решать эти три уравнения —

q ₂ = q ₁ b + q ₂ b + q ₃ b

= q ₁ b + q ₂ b + (q ₂ a) b (подставляя значение q ₃ )

= q ₁ b + q ₂ (b + ab)

= q ₁ b (b + ab) * (применение теоремы Ардена)

q ₁ = q ₁ a + q ₃ a + ε

= q ₁ a + q ₂ aa + ε (Подставляя значение q ₃ )

= q ₁ a + q ₁ b (b + ab *) aa + ε (Подставляя значение q ₂ )

= q ₁ (a + b (b + ab) * aa) + ε

= ε (a + b (b + ab) * aa) *

= (a + b (b + ab) * aa) *

Следовательно, регулярное выражение имеет вид (a + b (b + ab) * aa) *.

проблема

Построить регулярное выражение, соответствующее автоматам, приведенным ниже —

Решение —

Здесь начальное состояние q _1, а конечное состояние q ₂

Теперь запишем уравнения —

q ₁ = q ₁ 0 + ε

q ₂ = q ₁ 1 + q ₂ 0

q ₃ = q ₂ 1 + q ₃ 0 + q ₃ 1

Теперь мы будем решать эти три уравнения —

q ₁ = ε0 * [As, εR = R]

Итак, q ₁ = 0 *

q ₂ = 0 * 1 + q ₂ 0

Итак, q ₂ = 0 * 1 (0) * [по теореме Ардена]

Следовательно, регулярное выражение 0 * 10 *.

Строительство ТВС из РЭ

Мы можем использовать конструкцию Томпсона, чтобы найти конечный автомат по регулярному выражению. Мы сведем регулярное выражение к наименьшим регулярным выражениям и преобразуем их в NFA и, наконец, в DFA.

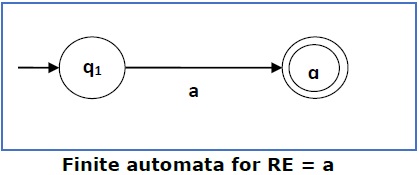
Вот некоторые основные выражения RA:

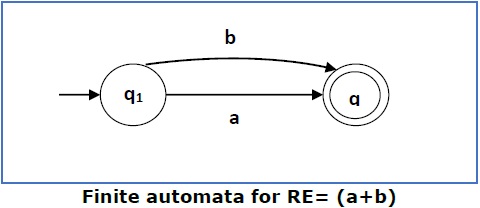
Случай 1 — Для регулярного выражения ‘a’ мы можем построить следующую FA —

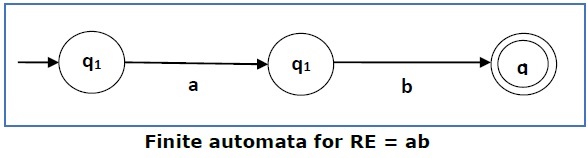
Случай 2 — Для регулярного выражения ‘ab’ мы можем построить следующую FA —

Случай 3 — Для регулярного выражения (a + b) мы можем построить следующую FA —

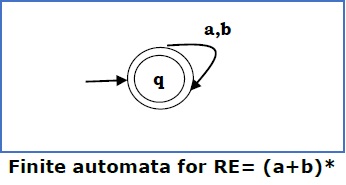
Случай 4 — Для регулярного выражения (a + b) * мы можем построить следующую FA —

метод

Шаг 1 Создайте NFA с нулевыми движениями из заданного регулярного выражения.

Шаг 2 Удалите нулевой переход из NFA и преобразуйте его в эквивалентный DFA.

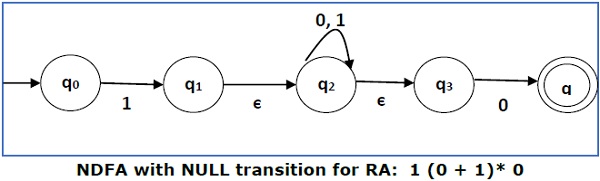
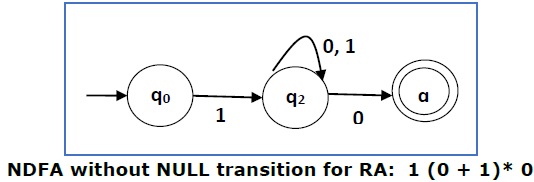
проблема

Преобразовать следующий RA в его эквивалентный DFA — 1 (0 + 1) * 0

Решение

Мы объединяем три выражения «1», «(0 + 1) *» и «0»

Теперь мы удалим ε- переходы. После того как мы удалим ε- переходы из NDFA, мы получим следующее —

Это NDFA, соответствующий RE — 1 (0 + 1) * 0. Если вы хотите преобразовать его в DFA, просто примените метод преобразования NDFA в DFA, описанный в главе 1.

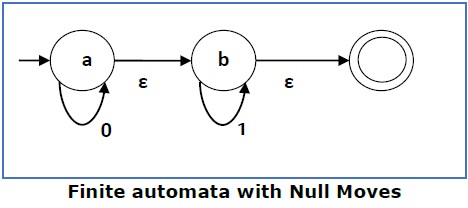
Конечные автоматы с нулевыми ходами (NFA-ε)

Конечный автомат с нулевыми ходами (FA-ε) проходит не только после ввода входных данных из набора алфавитов, но и без какого-либо входного символа. Этот переход без ввода называется нулевым ходом .

NFA-ε формально представлен 5-кортежем (Q, ∑, δ, q ₀ , F), состоящим из

• Q — конечное множество состояний

• ∑ — конечный набор входных символов

• δ — функция перехода δ: Q × (∑ ∪ {ε}) → 2 ^Q

• q ₀ — начальное состояние q ₀ ∈ Q

• F — множество конечных состояний / состояний Q (F⊆Q).

Q — конечное множество состояний

∑ — конечный набор входных символов

δ — функция перехода δ: Q × (∑ ∪ {ε}) → 2 ^Q

q ₀ — начальное состояние q ₀ ∈ Q

F — множество конечных состояний / состояний Q (F⊆Q).

Выше (FA-ε) принимает набор строк — {0, 1, 01}

Удаление нулевых ходов из конечных автоматов

Если в NDFA есть move-перемещение между вершиной X к вершине Y, мы можем удалить его, используя следующие шаги:

• Найти все исходящие ребра от Y.
• Скопируйте все эти ребра, начиная с X, не меняя метки ребер.
• Если X — начальное состояние, сделайте Y также начальным состоянием.
• Если Y — конечное состояние, сделайте X также конечным состоянием.

проблема

Преобразуйте следующие NFA-ε в NFA без нулевого хода.

Решение

Шаг 1 —

Здесь ε-переход находится между q ₁ и q ₂ , поэтому пусть q ₁ является X, а q _f является Y.

Здесь исходящие ребра из q _f равны q _f для входов 0 и 1.

Шаг 2 —

Теперь мы скопируем все эти ребра из q _1, не меняя ребер из q _f, и получим следующий FA —

Шаг 3 —

Здесь q ₁ — начальное состояние, поэтому мы делаем q _f также начальным состоянием.

Таким образом, ФА становится

Шаг 4 —

Здесь q _f — конечное состояние, поэтому мы делаем q ₁ также конечным состоянием.

Таким образом, ФА становится

Насосная лемма для регулярных грамматик

теорема

Пусть L обычный язык. Тогда существует постоянная ‘c’ такая, что для каждой строки w в L —

| ш | ≥ c

Мы можем разбить w на три строки, w = xyz , так что —

• | У | > 0
• | Х | ≤ c
• Для всех k ≥ 0 строка xy ^k z также находится в L.

Применение насосной леммы

Лемма накачки должна применяться, чтобы показать, что некоторые языки не являются регулярными. Это никогда не должно использоваться, чтобы показать, что язык является регулярным.

• Если L регулярно, то оно удовлетворяет лемме о накачке.

• Если L не удовлетворяет лемме накачки, она нерегулярна.

Если L регулярно, то оно удовлетворяет лемме о накачке.

Если L не удовлетворяет лемме накачки, она нерегулярна.

Способ доказать, что язык L не является регулярным

• Сначала мы должны предположить, что L регулярно.

• Таким образом, лемма прокачки должна выполняться для L.

• Используйте лемму прокачки, чтобы получить противоречие —

  • Выберите w так , чтобы | w | ≥ c

  • Выберите y так , чтобы | y | ≥ 1

  • Выберите x так , чтобы | xy | ≤ c

  • Назначьте оставшуюся строку z.

  • Выберите k так, чтобы полученная строка не была в L.

Сначала мы должны предположить, что L регулярно.

Таким образом, лемма прокачки должна выполняться для L.

Используйте лемму прокачки, чтобы получить противоречие —

Выберите w так , чтобы | w | ≥ c

Выберите y так , чтобы | y | ≥ 1

Выберите x так , чтобы | xy | ≤ c

Назначьте оставшуюся строку z.

Выберите k так, чтобы полученная строка не была в L.

Следовательно, L не является регулярным.

проблема

Докажите, что L = {a ⁱ b ⁱ | i ≥ 0} не является регулярным.

Решение —

• Сначала предположим, что L регулярно, а n — число состояний.

• Пусть w = a ⁿ b ⁿ . Таким образом | w | = 2n ≥ n.

• Прокачивая лемму, пусть w = xyz, где | xy | ≤ н.

• Пусть x = a ^p , y = a ^q и z = a ^r b ⁿ , где p + q + r = n, p ≠ 0, q ≠ 0, r ≠ 0. Таким образом, | y | ≠ 0.

• Пусть k = 2. Тогда xy ² z = a ^p a ^2q a ^r b ⁿ .

• Номер as = (p + 2q + r) = (p + q + r) + q = n + q

• Следовательно, xy ² z = a ^{n + q} b ⁿ . Поскольку q ≠ 0, xy ² z не имеет формы a ⁿ b ⁿ .

• Таким образом, xy ² z не входит в L. Следовательно, L не является регулярным.

Сначала предположим, что L регулярно, а n — число состояний.

Пусть w = a ⁿ b ⁿ . Таким образом | w | = 2n ≥ n.

Прокачивая лемму, пусть w = xyz, где | xy | ≤ н.

Пусть x = a ^p , y = a ^q и z = a ^r b ⁿ , где p + q + r = n, p ≠ 0, q ≠ 0, r ≠ 0. Таким образом, | y | ≠ 0.

Пусть k = 2. Тогда xy ² z = a ^p a ^2q a ^r b ⁿ .

Номер as = (p + 2q + r) = (p + q + r) + q = n + q

Следовательно, xy ² z = a ^{n + q} b ⁿ . Поскольку q ≠ 0, xy ² z не имеет формы a ⁿ b ⁿ .

Таким образом, xy ² z не входит в L. Следовательно, L не является регулярным.

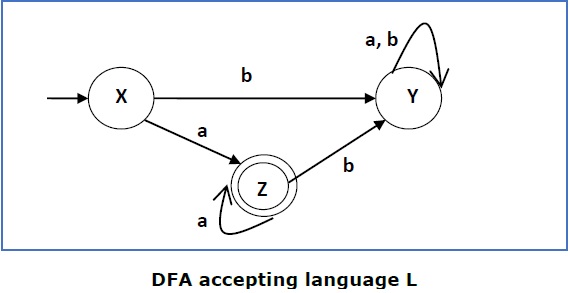
DFA Дополнение

Если (Q, ∑, δ, q ₀ , F) — DFA, который принимает язык L, то дополнение DFA может быть получено путем замены его принимающих состояний на неприемлемые и наоборот.

Мы возьмем пример и уточним это ниже —

Это DFA принимает язык

L = {a, aa, aaa, ………….}

по алфавиту

∑ = {a, b}

Итак, RE = ⁺ .

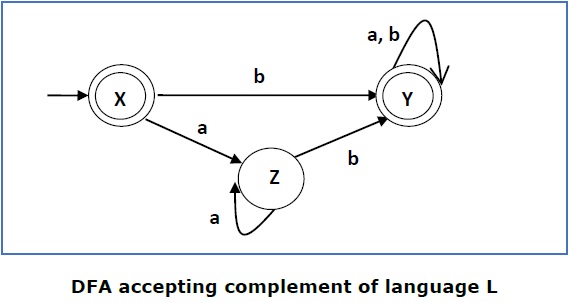
Теперь мы поменяем его принимающие состояния на непринятые и наоборот и получим следующее:

Это DFA принимает язык

Ľ = {ε, b, ab, bb, ba, ……………}

по алфавиту

∑ = {a, b}

Примечание. Если мы хотим дополнить NFA, мы должны сначала преобразовать его в DFA, а затем поменять местами, как в предыдущем методе.

Введение в контекстную грамматику

Определение — контекстно-свободная грамматика (CFG), состоящая из конечного набора правил грамматики, представляет собой четверку (N, T, P, S), где

• N представляет собой набор нетерминальных символов.

• T — это набор терминалов, где N ∩ T = NULL.

• P — это набор правил, P: N → (N ∪ T) * , т. Е. Левая часть производственного правила P имеет любой правый или левый контекст.

• S — начальный символ.

N представляет собой набор нетерминальных символов.

T — это набор терминалов, где N ∩ T = NULL.

P — это набор правил, P: N → (N ∪ T) * , т. Е. Левая часть производственного правила P имеет любой правый или левый контекст.

S — начальный символ.

пример

• Грамматика ({A}, {a, b, c}, P, A), P: A → aA, A → abc.
• Грамматика ({S, a, b}, {a, b}, P, S), P: S → aSa, S → bSb, S → ε
• Грамматика ({S, F}, {0, 1}, P, S), P: S → 00S | 11F, F → 00F | ε

Генерация дерева деривации

Дерево деривации или дерево разбора — это упорядоченное корневое дерево, которое графически представляет семантическую информацию в виде строки, полученной из контекстно-свободной грамматики.

Техника Представления

• Корневая вершина — должна быть помечена начальным символом.

• Вершина — помечена нетерминальным символом.

• Листья — помечены терминальным символом или ε.

Корневая вершина — должна быть помечена начальным символом.

Вершина — помечена нетерминальным символом.

Листья — помечены терминальным символом или ε.

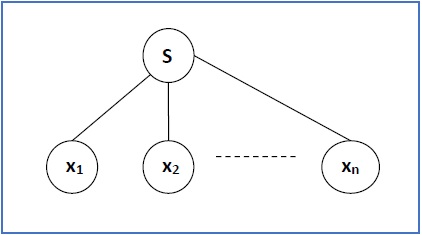
Если S → x ₁ x ₂ …… x _n является правилом производства в CFG, то дерево разбора / дерево деривации будет выглядеть следующим образом:

Существует два разных подхода для построения деривационного дерева:

Нисходящий подход —

• Начинается с начального символа S

• Спускается к листьям дерева, используя продукцию

Начинается с начального символа S

Спускается к листьям дерева, используя продукцию

Подход снизу вверх —

• Начинается с листьев дерева

• Идет вверх к корню, который является начальным символом S

Начинается с листьев дерева

Идет вверх к корню, который является начальным символом S

Вывод или урожайность дерева

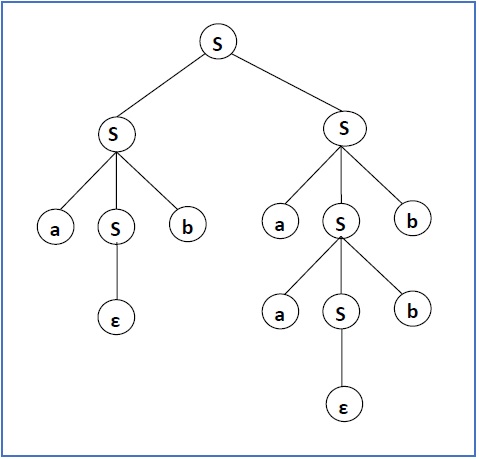
Деривация или выход дерева разбора — это последняя строка, полученная путем объединения меток листьев дерева слева направо, игнорируя значения Null. Однако, если все листья равны нулю, деривация равна нулю.

пример

Пусть CFG {N, T, P, S} будет

N = {S}, T = {a, b}, начальный символ = S, P = S → SS | aSb | ε

Одним из производных от вышеупомянутого CFG является «abaabb»

S → SS → aSbS → abS → abaSb → abaaSbb → abaabb

Форма предложения и Дерево частичного деривации

Частичное дерево деривации является поддеревом дерева деривации / дерева разбора, так что либо все его дочерние элементы находятся в поддереве, либо ни один из них не находится в поддереве.

пример

Если в любом CFG производства —

S → AB, A → aaA | ε, B → Bb | ε

Частичное дерево деривации может быть следующим:

Если дерево частичного деривации содержит корень S, оно называется формой предложения . Вышеуказанное поддерево также в форме предложения.

Самый левый и самый правый вывод строки

• Самый левый вывод — самый левый вывод получается путем применения производства к самой левой переменной на каждом шаге.

• Крайний правый вывод — Крайний правый вывод получается путем применения производного к самой правой переменной на каждом шаге.

Самый левый вывод — самый левый вывод получается путем применения производства к самой левой переменной на каждом шаге.

Крайний правый вывод — Крайний правый вывод получается путем применения производного к самой правой переменной на каждом шаге.

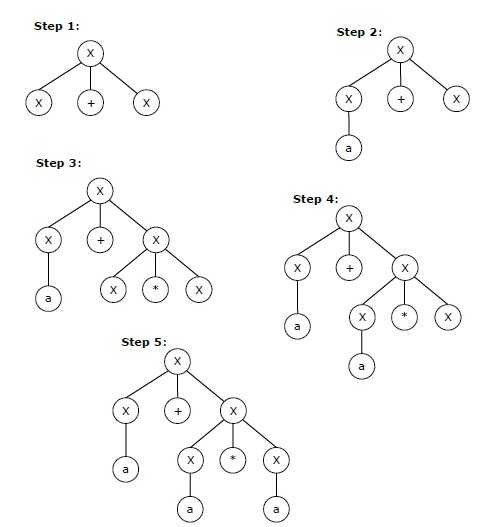
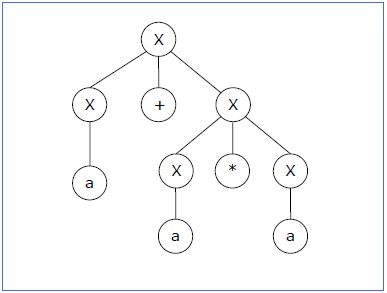
пример

Пусть любой набор правил производства в CFG будет

X → X + X | X * X | X |

над алфавитом {а}.

Крайний левый вывод для строки «a + a * a» может быть —

X → X + X → a + X → a + X * X → a + a * X → a + a * a

Пошаговое извлечение вышеуказанной строки показано ниже:

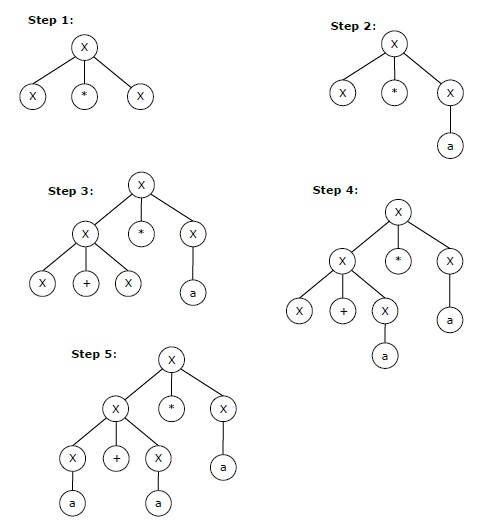
Самый правый вывод для приведенной выше строки «a + a * a» может быть —

X → X * X → X * a → X + X * a → X + a * a → a + a * a

Пошаговое извлечение вышеуказанной строки показано ниже:

Левая и правая рекурсивные грамматики

В не зависящей от контекста грамматике G , если существует произведение в форме X → Xa, где X — нетерминал, а ‘a’ — строка терминалов, это называется леворекурсивным произведением . Грамматика с левой рекурсивной продукцией называется левой рекурсивной грамматикой .

И если в не зависящей от контекста грамматике G , если есть произведение, имеет вид X → aX, где X — нетерминал, а ‘a’ — строка терминалов, это называется правильным рекурсивным произведением . Правильная рекурсивная грамматика называется правильной рекурсивной грамматикой .

Неоднозначность в контекстно-свободных грамматиках

Если у не зависящей от контекста грамматики G есть несколько деривационных деревьев для некоторой строки w ∈ L (G) , она называется неоднозначной грамматикой . Для некоторой строки, сгенерированной из этой грамматики, существует несколько производных справа и слева.

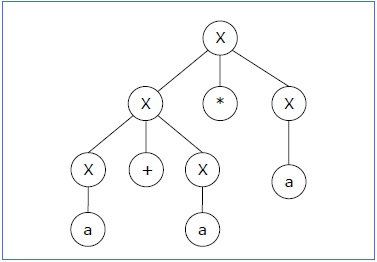
проблема

Проверьте, соответствует ли грамматика G правилам производства —

X → X + X | X * X | X |

неоднозначно или нет.

Решение

Давайте выясним дерево деривации для строки «a + a * a». У него два крайних левых вывода.

Вывод 1 — X → X + X → a + X → a + X * X → a + a * X → a + a * a

Разобрать дерево 1 —

Вывод 2 — X → X * X → X + X * X → a + X * X → a + a * X → a + a * a

Разобрать дерево 2 —

Поскольку для одной строки «a + a * a» существует два дерева разбора, грамматика G неоднозначна.

Собственность закрытия КЛЛ

Контекстные языки закрыты под —

• союз
• конкатенация
• Клини Стар операция

союз

Пусть L ₁ и L ₂ будут двумя контекстно-свободными языками. Тогда L ₁ ∪ L ₂ также не зависит от контекста.

пример

Пусть L ₁ = {a ⁿ b ⁿ , n> 0}. Соответствующая грамматика G ₁ будет иметь вид P: S1 → aAb | ab

Пусть L ₂ = {c ^m d ^m , m ≥ 0}. Соответствующая грамматика G ₂ будет иметь вид P: S2 → cBb | ε

Объединение L ₁ и L ₂ , L = L ₁ ∪ L ₂ = {a ⁿ b ⁿ } ∪ {c ^m d ^m }

Соответствующая грамматика G будет иметь дополнительное произведение S → S1 | S2

конкатенация

Если L ₁ и L ₂ являются контекстно-свободными языками, то L ₁ L ₂ также не зависит от контекста.

пример

Союз языков L ₁ и L ₂ , L = L _1, L ₂ = {a ⁿ b ⁿ c ^m d ^m }

Соответствующая грамматика G будет иметь дополнительное произведение S → S1 S2

Клини Стар

Если L является контекстно-свободным языком, то L * также не зависит от контекста.

пример

Пусть L = {a ⁿ b ⁿ , n ≥ 0}. Соответствующая грамматика G будет иметь вид P: S → aAb | ε

Клини Стар L ₁ = {a ⁿ b ⁿ } *

Соответствующая грамматика G ₁ будет иметь дополнительные произведения S1 → SS ₁ | ε

Контекстно-свободные языки не закрыты под —

• Пересечение — Если L1 и L2 являются контекстно-свободными языками, то L1 ∩ L2 не обязательно является контекстно-свободным.

• Пересечение с обычным языком — если L1 является обычным языком, а L2 является языком без контекста, то L1 ∩ L2 является языком без контекста.

• Дополнение — если L1 является контекстно-свободным языком, то L1 ‘может не быть контекстно-свободным.

Пересечение — Если L1 и L2 являются контекстно-свободными языками, то L1 ∩ L2 не обязательно является контекстно-свободным.

Пересечение с обычным языком — если L1 является обычным языком, а L2 является языком без контекста, то L1 ∩ L2 является языком без контекста.

Дополнение — если L1 является контекстно-свободным языком, то L1 ‘может не быть контекстно-свободным.

Упрощение CFG

В CFG может случиться так, что все производственные правила и символы не нужны для получения строк. Кроме того, могут быть нулевые производства и единичные производства. Устранение этих производств и символов называется упрощением CFG . Упрощение состоит из следующих этапов:

• Снижение CFG
• Вывоз единицы продукции
• Удаление Нулевых Продукций

Снижение CFG

CFG снижаются в два этапа —

Фаза 1 — Вывод эквивалентной грамматики G ‘ из CFG, G , так что каждая переменная выводит некоторую терминальную строку.

Процедура деривации —

Шаг 1 — Включите все символы W ₁ , которые выводят некоторый терминал и инициализируют i = 1 .

Шаг 2 — Включите все символы W _{i + 1} , которые выводят W _i .

Шаг 3 — Увеличить i и повторять Шаг 2, пока W _{i + 1} = W _i .

Шаг 4 — Включите все производственные правила, в которых есть W _i .

Этап 2 — Вывод эквивалентной грамматики G ” из CFG G ‘ , так что каждый символ появляется в форме предложения.

Процедура деривации —

Шаг 1 — Включите начальный символ в Y ₁ и инициализируйте i = 1 .

Шаг 2. Включите все символы Y _{i + 1} , которые могут быть получены из Y _i, и включите все производственные правила, которые были применены.

Шаг 3 — Увеличьте i и повторяйте Шаг 2, пока Y _{i + 1} = Y _i .

проблема

Найдите приведенную грамматику, эквивалентную грамматике G, имеющей правила производства, P: S → AC | B, A → a, C → c | BC, E → aA | е

Решение

Фаза 1 —

T = {a, c, e}

W ₁ = {A, C, E} из правил A → a, C → c и E → aA

W ₂ = {A, C, E} U {S} из правила S → AC

W ₃ = {A, C, E, S} U ∅

Поскольку W ₂ = W ₃ , мы можем вывести G ‘как —

G ‘= {{A, C, E, S}, {a, c, e}, P, {S}}

где P: S → AC, A → a, C → c, E → aA | е

Фаза 2 —

Y ₁ = {S}

Y ₂ = {S, A, C} из правила S → AC

Y ₃ = {S, A, C, a, c} из правил A → a и C → c

Y ₄ = {S, A, C, a, c}

Поскольку Y ₃ = Y ₄ , мы можем вывести G ”как —

G ”= {{A, C, S}, {a, c}, P, {S}}

где P: S → AC, A → a, C → c

Вывоз единицы продукции

Любое производственное правило в форме A → B, где A, B ∈ Non-Terminal, называется единичным производством. ,

Процедура удаления —

Шаг 1 — Чтобы удалить A → B , добавьте производство A → x к правилу грамматики всякий раз, когда B → x встречается в грамматике. [x ∈ Terminal, x может быть нулевым]

Шаг 2 — Удалить A → B из грамматики.

Шаг 3 — Повторите с шага 1, пока все производства юнитов не будут удалены.

проблема

Удалить единицу продукции из следующего —

S → XY, X → a, Y → Z | b, Z → M, M → N, N → a

Решение —

В грамматике есть 3 единичных произведения —

Y → Z, Z → M и M → N

Сначала мы удалим M → N.

При N → a мы добавляем M → a, а M → N удаляется.

Производственный набор становится

S → XY, X → a, Y → Z | b, Z → M, M → a, N → a

Теперь мы удалим Z → M.

При M → a мы добавляем Z → a, а Z → M удаляется.

Производственный набор становится

S → XY, X → a, Y → Z | b, Z → a, M → a, N → a

Теперь мы удалим Y → Z.

При Z → a мы добавляем Y → a, а Y → Z удаляется.

Производственный набор становится

S → XY, X → a, Y → a | b, Z → a, M → a, N → a

Теперь Z, M и N недоступны, поэтому мы можем их удалить.

Конечный CFG — единичное производство бесплатно —

S → XY, X → a, Y → a | б

Удаление Нулевых Продукций

В CFG нетерминальный символ «A» является переменной, допускающей значение NULL, если существует произведение A → ε или существует деривация, которая начинается в A и в конце заканчивается

ε: A → …….… → ε

Процедура удаления

Шаг 1 — Узнайте обнуляемые нетерминальные переменные, которые выводят ε.

Шаг 2 — Для каждого производства A → a построим все производства A → x, где x получается из «a» , удаляя один или несколько нетерминалов из шага 1.

Шаг 3 — Объедините оригинальные произведения с результатом шага 2 и удалите ε — произведения .

проблема

Удалить нулевую продукцию из следующего —

S → ASA | АБ | b, A → B, B → b | ∈

Решение —

Есть две обнуляемые переменные — A и B

Сначала мы удалим B → ε.

После удаления B → ε производственный набор становится —

S → ASA | АБ | б | a, A ε B | б | & эпсилон, B → b

Теперь мы удалим A → ε.

После удаления A → ε производственный набор становится —

S → ASA | АБ | б | а | SA | AS | S, A → B | б, б → б

Это окончательный набор продукции без нулевого перехода.

Хомская нормальная форма

CFG находится в нормальной форме Хомского, если продукция находится в следующих формах —

• А → а
• A → BC
• S → ε

где A, B и C не являются терминалами, а a являются терминалами.

Алгоритм преобразования в нормальную форму Хомского —

Шаг 1 — Если начальный символ S встречается справа, создайте новый начальный символ S ‘ и новый производственный S’ → S.

Шаг 2 — Удалить нулевые произведения. (Использование алгоритма удаления продукции Null, обсуждавшегося ранее)

Шаг 3 — Удалить единицу продукции. (Использование алгоритма удаления производства блока обсуждалось ранее)

Шаг 4 — Заменить каждое производство A → B ₁ … B _n, где n> 2, на A → B ₁ C, где C → B ₂ … B _n . Повторите этот шаг для всех произведений, имеющих два или более символов в правой части.

Шаг 5 — Если правая сторона любого производства имеет вид A → aB, где a является терминалом, а A, B нетерминальным, то производство заменяется на A → XB и X → a . Повторите этот шаг для каждого производства, которое имеет вид A → aB .

проблема

Конвертировать следующие CFG в CNF

S → ASA | aB, A → B | S, B → b | ε

Решение

(1) Поскольку S появляется в RHS, мы добавляем новое состояние S _0, а S ₀ → S добавляется в производственный набор, и оно становится —

S ₀ → S, S → ASA | aB, A → B | S, B → b | ∈

(2) Теперь мы удалим нулевые произведения —

B → ∈ и A → ∈

После удаления B → ε производственный набор становится —

S ₀ → S, S → ASA | АБ | a, A → B | S | ∈, B → b

После удаления A → ∈ производственный набор становится —

S ₀ → S, S → ASA | АБ | а | AS | SA | S, A → B | S, B → b

(3) Теперь мы удалим единицу продукции.

После удаления S → S, производственный набор становится —

S ₀ → S, S → ASA | АБ | а | AS | SA, A → B | S, B → b

После удаления S ₀ → S, производственный набор становится —

S ₀ → ASA | АБ | а | AS | SA, S → ASA | АБ | а | AS | SA

A → B | S, B → b

После удаления A → B производственный набор становится —

S ₀ → ASA | АБ | а | AS | SA, S → ASA | АБ | а | AS | SA

A → S | б

B → b

После удаления A → S производственный набор становится —

S ₀ → ASA | АБ | а | AS | SA, S → ASA | АБ | а | AS | SA

A → b | ASA | АБ | а | AS | SA, B → b

(4) Теперь мы узнаем более двух переменных в RHS

Здесь S ₀ → ASA, S → ASA, A → ASA нарушает два нетерминала в RHS

Следовательно, мы применим шаг 4 и шаг 5, чтобы получить следующий конечный производственный набор, который находится в CNF —

S ₀ → AX | АБ | а | AS | SA

S → AX | АБ | а | AS | SA

A → b | AX | АБ | а | AS | SA

B → b

X → SA

(5) Мы должны изменить произведения S ₀ → aB, S → aB, A → aB

И окончательный комплект производства становится —

S ₀ → AX | YB | а | AS | SA

S → AX | YB | а | AS | SA

A → b A → b | AX | YB | а | AS | SA

B → b

X → SA

Y → a

Грайбах Нормальная форма

CFG находится в нормальной форме Грейбаха, если продукция представлена ​​в следующих формах:

A → b

A → bD ₁ … D _n

S → ε

где A, D ₁ , …., D _{n не} являются терминалами, а b является терминалом.

Алгоритм для преобразования CFG в нормальную форму Грейбаха

Шаг 1 — Если начальный символ S встречается справа, создайте новый начальный символ S ‘ и новый производственный S’ → S.

Шаг 2 — Удалить нулевые произведения. (Использование алгоритма удаления продукции Null, обсуждавшегося ранее)

Шаг 3 — Удалить единицу продукции. (Использование алгоритма удаления производства блока обсуждалось ранее)

Шаг 4 — Удалить все прямые и косвенные левые рекурсии.

Шаг 5 — Делайте правильные замены произведений, чтобы преобразовать его в правильную форму GNF.

проблема

Конвертировать следующие CFG в CNF

S → XY | Xn | п

X → mX | м

Y → Xn | о

Решение

Здесь S не отображается справа от любого производства, и в наборе правил производства нет единичных или нулевых производств. Итак, мы можем пропустить Шаг 1 до Шаг 3.

Шаг 4

Теперь после замены

X в S → XY | Xo | п

с

мх | м

мы получаем

S → mXY | мг | mXo | мо | п.

И после замены

X в Y → X _n | о

с правой стороны

X → mX | м

мы получаем

Y → mXn | мн | о.

Два новых произведения O → o и P → p добавляются к производственному набору, а затем мы подошли к финальному GNF следующим образом:

S → mXY | мг | mXC | мс | п

X → mX | м

Y → mXD | мд | о

O → o

P → p

Насосная лемма для CFG

лемма

Если L является контекстно-свободным языком, существует длина накачки p такая, что любую строку w ∈ L длины ≥ p можно записать как w = uvxyz , где vy ≠ ε , | vxy | ≤ p , и для всех i ≥ 0 uv ⁱ xy ⁱ z ∈ L.

Применение насосной леммы

Насосная лемма используется для проверки, является ли грамматика контекстно-свободной или нет. Давайте возьмем пример и покажем, как он проверен.

проблема

Узнайте, является ли язык L = {x ⁿ y ⁿ z ⁿ | n ≥ 1} не зависит от контекста или нет.

Решение

Пусть L не зависит от контекста. Тогда L должна удовлетворять лемме накачки.

Сначала выберите номер n леммы прокачки. Тогда возьмите z в качестве 0 ⁿ 1 ⁿ 2 ⁿ .

Разбить z в uvwxy, где

| VWX | ≤ n и vx ≠ ε.

Следовательно, vwx не может включать в себя как 0, так и 2, поскольку последние 0 и первые 2 расположены на расстоянии не менее (n + 1) позиций. Есть два случая —

Случай 1 — vwx не имеет 2s. Тогда у vx есть только 0 и 1. Тогда uwy , который должен быть в L , имеет n 2s, но меньше, чем n 0s или 1s.

Случай 2 — vwx не имеет нулей.

Здесь возникает противоречие.

Следовательно, L не является контекстно-свободным языком.

Pushdown Автоматы Введение

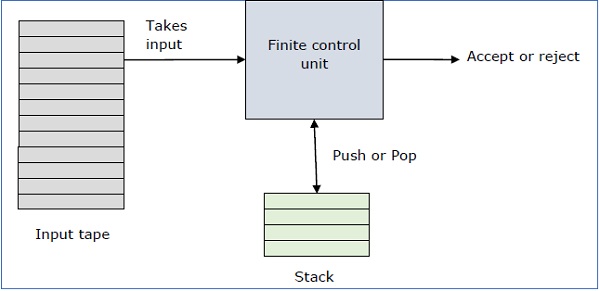
Базовая структура КПК

Автомат pushdown — это способ реализовать контекстно-свободную грамматику аналогично тому, как мы проектируем DFA для обычной грамматики. DFA может запоминать ограниченное количество информации, но PDA может запоминать бесконечное количество информации.

По сути, автомат с нажатием кнопки —

«Конечный автомат» + «стек»

Автомат с нажатием кнопки состоит из трех компонентов:

• входная лента,
• блок управления и
• стек с бесконечным размером.

Голова стека сканирует верхний символ стека.

Стек выполняет две операции —

• Нажмите — новый символ добавлен вверху.

• Pop — верхний символ читается и удаляется.

Нажмите — новый символ добавлен вверху.

Pop — верхний символ читается и удаляется.

КПК может или не может прочитать входной символ, но он должен читать вершину стека при каждом переходе.

КПК может быть формально описан как 7-кортеж (Q, ∑, S, δ, q ₀ , I, F) —

• Q — конечное число состояний

• Input является входным алфавитом

• S — символы стека

• δ — функция перехода: Q × (∪ ∪ {ε}) × S × Q × S *

• q ₀ — начальное состояние (q ₀ ∈ Q)

• I — начальный символ вершины стека (I ∈ S)

• F — множество принимающих состояний (F ∈ Q)

Q — конечное число состояний

Input является входным алфавитом

S — символы стека

δ — функция перехода: Q × (∪ ∪ {ε}) × S × Q × S *

q ₀ — начальное состояние (q ₀ ∈ Q)

I — начальный символ вершины стека (I ∈ S)

F — множество принимающих состояний (F ∈ Q)

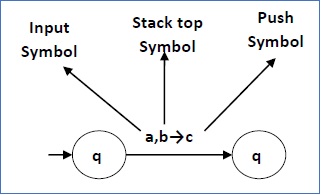
Следующая диаграмма показывает переход в КПК из состояния q ₁ в состояние q ₂ , помеченный как a, b → c —

Это означает, что в состоянии q ₁ , если мы сталкиваемся с входной строкой ‘a’ и верхним символом стека является ‘b’ , то мы выталкиваем ‘ b’ , помещаем ‘c’ в верхнюю часть стека и переходим в состояние q ₂ .

Терминологии, связанные с КПК

Мгновенное описание

Мгновенное описание (ID) КПК представлено триплетом (q, w, s), где

• q это состояние

• w — неиспользованный ввод

• s — содержимое стека

q это состояние

w — неиспользованный ввод

s — содержимое стека

Турникет Нотация

Обозначение «турникет» используется для соединения пар идентификаторов, которые представляют один или несколько ходов КПК. Процесс перехода обозначается символом турникета «⊢».

Рассмотрим КПК (Q, ∑, S, δ, q ₀ , I, F). Переход может быть математически представлен следующими обозначениями турникета —

(p, aw, Tβ) ⊢ (q, w, αb)

Это подразумевает, что при переходе из состояния p в состояние q используется входной символ «a» , а вершина стека «T» заменяется новой строкой «α» .

Примечание. Если нам требуется ноль или более ходов КПК, мы должны использовать для него символ (⊢ *).

Приемка автоматов

Существует два разных способа определения приемлемости КПК.

Окончательная государственная приемлемость

В приемлемости конечного состояния КПК принимает строку, когда после прочтения всей строки КПК находится в конечном состоянии. Из начального состояния мы можем делать ходы, которые заканчиваются в конечном состоянии с любыми значениями стека. Значения стека не имеют значения, пока мы не окажемся в конечном состоянии.

Для КПК (Q, ∑, S, δ, q ₀ , I, F) язык, принятый множеством конечных состояний F, равен —

L (PDA) = {w | (q ₀ , w, I) ⊢ * (q, ε, x), q ∈ F}

для любой строки входного стека x .

Приемлемость пустого стека

Здесь КПК принимает строку, когда после чтения всей строки КПК опустошил свой стек.

Для КПК (Q, ∑, S, δ, q ₀ , I, F) язык, принятый пустым стеком, равен —

L (PDA) = {w | (q ₀ , w, I) ⊢ * (q, ε, ε), q ∈ Q}

пример

Построить КПК, который принимает L = {0 ⁿ 1 ⁿ | n ≥ 0}

Решение

Этот язык принимает L = {ε, 01, 0011, 000111, ………………………..}

Здесь, в этом примере, число «a» и «b» должно быть одинаковым.

• Сначала мы помещаем специальный символ «$» в пустой стек.

• Затем в состоянии q ₂ , если мы сталкиваемся с вводом 0 и top равен Null, мы помещаем 0 в стек. Это может повторяться. И если мы встретим ввод 1 и top равен 0, мы вытолкнем это 0.

• Затем в состоянии q ₃ , если мы сталкиваемся с входом 1 и top равен 0, мы выталкиваем это 0. Это также может повторяться. И если мы встретим ввод 1 и top равен 0, мы вытолкнем верхний элемент.

• Если в верхней части стека встречается специальный символ ‘$’, он выталкивается и, наконец, переходит в принимающее состояние q ₄ .

Сначала мы помещаем специальный символ «$» в пустой стек.

Затем в состоянии q ₂ , если мы сталкиваемся с вводом 0 и top равен Null, мы помещаем 0 в стек. Это может повторяться. И если мы встретим ввод 1 и top равен 0, мы вытолкнем это 0.

Затем в состоянии q ₃ , если мы сталкиваемся с входом 1 и top равен 0, мы выталкиваем это 0. Это также может повторяться. И если мы встретим ввод 1 и top равен 0, мы вытолкнем верхний элемент.

Если в верхней части стека встречается специальный символ ‘$’, он выталкивается и, наконец, переходит в принимающее состояние q ₄ .

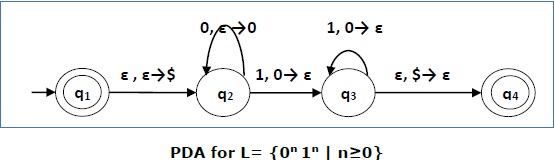
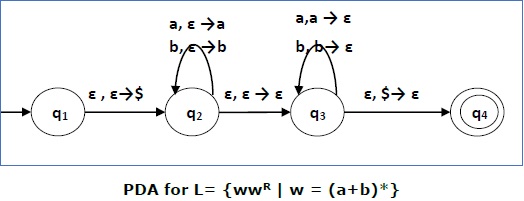
пример

Построить КПК, который принимает L = {ww ^R | w = (a + b) *}

Решение

Сначала мы помещаем специальный символ «$» в пустой стек. В состоянии q ₂ w читается. В состоянии q ₃ каждый 0 или 1 выталкивается, когда он соответствует входу. Если задан какой-либо другой вход, КПК перейдет в мертвое состояние. Когда мы достигаем этого специального символа ‘$’, мы переходим в принимающее состояние q ₄ .

КПК и контекстно-бесплатная грамматика

Если грамматика G не зависит от контекста, мы можем создать эквивалентный недетерминированный КПК, который принимает язык, который генерируется не зависящей от контекста грамматикой G. Парсер может быть построен для грамматики G.

Кроме того, если P является автоматом нажатия, может быть построена эквивалентная не зависящая от контекста грамматика G, где

L (G) = L (P)

В следующих двух темах мы обсудим, как перейти с КПК на CFG и наоборот.

Алгоритм нахождения КПК, соответствующего данному КФГ

Вход — A CFG, G = (V, T, P, S)

Выход — эквивалентный КПК, P = (Q, ∑, S, δ, q ₀ , I, F)

Шаг 1 — Преобразование производства CFG в GNF.

Шаг 2 — КПК будет иметь только одно состояние {q}.

Шаг 3 — Начальный символ CFG будет начальным символом в КПК.

Шаг 4 — Все нетерминалы CFG будут символами стека КПК, а все терминалы CFG будут входными символами КПК.

Шаг 5 — Для каждого производства в форме A → aX, где a является терминалом, а A, X являются комбинацией терминалов и нетерминалов, выполните переход δ (q, a, A) .

проблема

Построить КПК из следующего CFG.

G = ({S, X}, {a, b}, P, S)

где производства —

S → XS | ε, A → aXb | Ab | аб

Решение

Пусть эквивалентный КПК,

P = ({q}, {a, b}, {a, b, X, S}, δ, q, S)

где δ —

δ (q, ε, S) = {(q, XS), (q, ε)}

δ (q, ε, X) = {(q, aXb), (q, Xb), (q, ab)}

δ (q, a, a) = {(q, ε)}

δ (q, 1, 1) = {(q, ε)}

Алгоритм поиска CFG, соответствующего данному КПК

Вход — A CFG, G = (V, T, P, S)

Вывод — Эквивалентный PDA, P = (Q, ∑, S, δ, q ₀ , I, F), такой, что нетерминалы грамматики G будут {X _wx | w, x ∈ Q}, и начальное состояние будет A _{q0, F.}

Шаг 1 — Для каждого w, x, y, z ∈ Q, m ∈ S и a, b ∈ ∑, если δ (w, a, ε) содержит (y, m) и (z, b, m) содержит ( x, ε), добавьте правило производства X _wx → a X _yz b в грамматике G.

Шаг 2 — Для каждого w, x, y, z ∈ Q добавьте правило произведения X _wx → X _wy X _yx в грамматике G.

Шаг 3 — Для w ∈ Q добавьте производное правило X _ww → ε в грамматике G.

Pushdown автоматы и парсинг

Синтаксический анализ используется для получения строки с использованием правил производства грамматики. Он используется для проверки приемлемости строки. Компилятор используется для проверки правильности синтаксической строки. Парсер принимает входные данные и строит дерево разбора.

Парсер может быть двух типов:

• Анализатор сверху вниз — синтаксический анализ сверху вниз начинается с символа начала и выводит строку с использованием дерева синтаксического анализа.

• Анализатор снизу вверх — анализ снизу вверх начинается снизу строкой и доходит до начального символа с использованием дерева разбора.

Анализатор сверху вниз — синтаксический анализ сверху вниз начинается с символа начала и выводит строку с использованием дерева синтаксического анализа.

Анализатор снизу вверх — анализ снизу вверх начинается снизу строкой и доходит до начального символа с использованием дерева разбора.

Дизайн нисходящего парсера

Для анализа сверху вниз в КПК есть следующие четыре типа переходов:

• Наденьте нетерминал с левой стороны производства на вершину стека и нажмите на правую струну.

• Если верхний символ стека совпадает с читаемым символом ввода, вставьте его.

• Вставьте стартовый символ «S» в стек.

• Если входная строка полностью прочитана, а стек пуст, перейдите в конечное состояние «F».

Наденьте нетерминал с левой стороны производства на вершину стека и нажмите на правую струну.

Если верхний символ стека совпадает с читаемым символом ввода, вставьте его.

Вставьте стартовый символ «S» в стек.

Если входная строка полностью прочитана, а стек пуст, перейдите в конечное состояние «F».

пример

Разработайте анализатор сверху вниз для выражения «x + y * z» для грамматики G со следующими правилами производства:

P: S → S + X | X, X → X * Y | Y, Y → (S) | Я бы

Решение

Если КПК (Q, ∑, S, δ, q ₀ , I, F), то разбор сверху вниз —

(x + y * z, I) ⊢ (x + y * z, SI) ⊢ (x + y * z, S + XI) ⊢ (x + y * z, X + XI)

⊢ (x + y * z, Y + XI) ⊢ (x + y * z, x + XI) ⊢ (+ y * z, + XI) ⊢ (y * z, XI)

⊢ (y * z, X * YI) ⊢ (y * z, y * YI) ⊢ (* z, * YI) ⊢ (z, YI) ⊢ (z, zI) ⊢ (ε, I)

Дизайн снизу вверх парсера

Для анализа снизу вверх КПК имеет следующие четыре типа переходов:

• Вставьте текущий входной символ в стек.

• Замените правую часть производства в верхней части стека левой стороной.

• Если вершина стекового элемента совпадает с текущим входным символом, вставьте его.

• Если входная строка полностью прочитана и только если начальный символ «S» остается в стеке, вытолкните ее и перейдите в конечное состояние «F».

Вставьте текущий входной символ в стек.

Замените правую часть производства в верхней части стека левой стороной.

Если вершина стекового элемента совпадает с текущим входным символом, вставьте его.

Если входная строка полностью прочитана и только если начальный символ «S» остается в стеке, вытолкните ее и перейдите в конечное состояние «F».

пример

Разработайте анализатор сверху вниз для выражения «x + y * z» для грамматики G со следующими правилами производства:

P: S → S + X | X, X → X * Y | Y, Y → (S) | Я бы

Решение

Если КПК (Q, ∑, S, δ, q ₀ , I, F), то анализ снизу вверх —

(x + y * z, I) ⊢ (+ y * z, xI) ⊢ (+ y * z, YI) ⊢ (+ y * z, XI) ⊢ (+ y * z, SI)

⊢ (y * z, + SI) ⊢ (* z, y + SI) ⊢ (* z, Y + SI) ⊢ (* z, X + SI) ⊢ (z, * X + SI)

⊢ (ε, z * X + SI) ⊢ (ε, Y * X + SI) ⊢ (ε, X + SI) ⊢ (ε, SI)

Введение машины Тьюринга

Машина Тьюринга — это принимающее устройство, которое принимает языки (рекурсивно перечислимый набор), генерируемые грамматиками типа 0. Он был изобретен в 1936 году Аланом Тьюрингом.

Определение

Машина Тьюринга (ТМ) — это математическая модель, которая состоит из ленты бесконечной длины, разделенной на ячейки, в которые вводятся данные. Он состоит из головы, которая читает входную ленту. Государственный реестр хранит состояние машины Тьюринга. После прочтения входного символа он заменяется другим символом, его внутреннее состояние изменяется, и он перемещается из одной ячейки вправо или влево. Если TM достигает конечного состояния, входная строка принимается, в противном случае отклоняется.

ТМ можно формально описать как 7-кортеж (Q, X, ∑, δ, q ₀ , B, F), где —

• Q — конечное множество состояний

• X это ленточный алфавит

• ∑ является входным алфавитом

• δ — переходная функция; δ: Q × X → Q × X × {Сдвиг влево, сдвиг вправо}.

• q ₀ — начальное состояние

• B — это пустой символ

• F — множество конечных состояний

Q — конечное множество состояний

X это ленточный алфавит

∑ является входным алфавитом

δ — переходная функция; δ: Q × X → Q × X × {Сдвиг влево, сдвиг вправо}.

q ₀ — начальное состояние

B — это пустой символ

F — множество конечных состояний

Сравнение с предыдущим автоматом

В следующей таблице показано сравнение того, как машина Тьюринга отличается от Finite Automaton и Pushdown Automaton.

Машина	Структура данных стека	Детерминированный?
Конечный Автомат	Не Доступно	да
Pushdown Автомат	Последний вошел первый (ЛИФО)	нет
Машина Тьюринга	Бесконечная лента	да

Пример машины Тьюринга

Машина Тьюринга M = (Q, X, ∑, δ, q ₀ , B, F) с

• Q = {q ₀ , q ₁ , q ₂ , q _f }
• X = {a, b}
• ∑ = {1}
• q ₀ = {q ₀ }
• B = пустой символ
• F = {q _f }

δ определяется как —

Лента символ алфавита	Текущее состояние ‘q 0 ‘	Современное состояние ‘q 1 ‘	Современное состояние ‘q 2 ‘
	1Rq 1	1Lq 0	1 литр ф
б	1Lq 2	1Rq 1	1Rq f

Здесь переход 1Rq ₁ подразумевает, что символ записи равен 1, лента движется вправо, а следующее состояние — q ₁ . Аналогично, переход 1Lq ₂ подразумевает, что символ записи равен 1, лента перемещается влево, а следующее состояние — q ₂ .

Пространственно-временная сложность машины Тьюринга

Для машины Тьюринга под сложностью времени понимается мера количества перемещений ленты, когда машина инициализируется для некоторых входных символов, а сложность пространства — это количество ячеек записанной ленты.

Временная сложность всех разумных функций —

T (n) = O (n log n)

Пространственная сложность ТМ —

S (n) = O (n)

Принятый язык и определенный язык

ТМ принимает язык, если он входит в конечное состояние для любой входной строки w. Язык рекурсивно перечислим (генерируется грамматикой типа 0), если он принят машиной Тьюринга.

ТМ решает язык, если он его принимает, и переходит в состояние отклонения для любого ввода, не являющегося языком. Язык рекурсивен, если это решено машиной Тьюринга.

Могут быть случаи, когда ТМ не останавливается. Такая ТМ принимает язык, но не решает его.

Проектирование машины Тьюринга

Основные рекомендации по проектированию машины Тьюринга были объяснены ниже с помощью нескольких примеров.

Пример 1

Разработайте TM, чтобы распознавать все строки, состоящие из нечетного числа α.

Решение

Машина Тьюринга М может быть построена следующими движениями:

• Пусть q ₁ будет начальным состоянием.

• Если М в q ₁ ; при сканировании α он переходит в состояние q ₂ и записывает B (пусто).

• Если М в q ₂ ; при сканировании α он переходит в состояние q ₁ и записывает B (пусто).

• Из приведенных выше шагов мы можем видеть, что M переходит в состояние q _1, если сканирует четное число α, и входит в состояние q _2, если сканирует нечетное число α. Следовательно, q ₂ является единственным принимающим состоянием.

Пусть q ₁ будет начальным состоянием.

Если М в q ₁ ; при сканировании α он переходит в состояние q ₂ и записывает B (пусто).

Если М в q ₂ ; при сканировании α он переходит в состояние q ₁ и записывает B (пусто).

Из приведенных выше шагов мы можем видеть, что M переходит в состояние q _1, если сканирует четное число α, и входит в состояние q _2, если сканирует нечетное число α. Следовательно, q ₂ является единственным принимающим состоянием.

Следовательно,

M = {{q ₁ , q ₂ }, {1}, {1, B}, δ, q ₁ , B, {q ₂ }}

где δ определяется как —

Лента символ алфавита	Современное состояние ‘q 1 ‘	Современное состояние ‘q 2 ‘
α	BRq 2	BRq 1

Пример 2

Разработайте машину Тьюринга, которая читает строку, представляющую двоичное число, и удаляет все первые 0 в строке. Однако, если строка содержит только 0, она сохраняет один 0.

Решение

Предположим, что входная строка заканчивается пустым символом B на каждом конце строки.

Машина Тьюринга M может быть построена следующими способами:

• Пусть q ₀ будет начальным состоянием.

• Если M находится в q ₀ , при чтении 0 он перемещается вправо, входит в состояние q ₁ и стирает 0. При чтении 1 он входит в состояние q ₂ и перемещается вправо.

• Если M находится в q ₁ , при чтении 0 он перемещается вправо и стирает 0, т. Е. Заменяет 0 на B. Достигнув крайнего левого 1, он входит в q ₂ и движется вправо. Если он достигает B, то есть строка содержит только 0, она перемещается влево и входит в состояние q ₃ .

• Если M находится в q ₂ , при чтении 0 или 1 он перемещается вправо. Достигнув B, он двигается влево и входит в состояние q ₄ . Это подтверждает, что строка содержит только 0 и 1.

• Если M находится в q ₃ , он заменяет B на 0, перемещается влево и достигает конечного состояния q _f .

• Если M находится в q ₄ , при чтении 0 или 1 он перемещается влево. По достижении начала строки, т. Е. Когда она читает B, она достигает конечного состояния q _f .

Пусть q ₀ будет начальным состоянием.

Если M находится в q ₀ , при чтении 0 он перемещается вправо, входит в состояние q ₁ и стирает 0. При чтении 1 он входит в состояние q ₂ и перемещается вправо.

Если M находится в q ₁ , при чтении 0 он перемещается вправо и стирает 0, т. Е. Заменяет 0 на B. Достигнув крайнего левого 1, он входит в q ₂ и движется вправо. Если он достигает B, то есть строка содержит только 0, она перемещается влево и входит в состояние q ₃ .

Если M находится в q ₂ , при чтении 0 или 1 он перемещается вправо. Достигнув B, он двигается влево и входит в состояние q ₄ . Это подтверждает, что строка содержит только 0 и 1.

Если M находится в q ₃ , он заменяет B на 0, перемещается влево и достигает конечного состояния q _f .

Если M находится в q ₄ , при чтении 0 или 1 он перемещается влево. По достижении начала строки, т. Е. Когда она читает B, она достигает конечного состояния q _f .

Следовательно,

M = {{q ₀ , q ₁ , q ₂ , q ₃ , q ₄ , q _f }, {0,1, B}, {1, B}, δ, q ₀ , B, {q _f }}

где δ определяется как —

Лента символ алфавита	Текущее состояние ‘q 0 ‘	Современное состояние ‘q 1 ‘	Современное состояние ‘q 2 ‘	Современное состояние ‘q 3 ‘	Современное состояние ‘q 4 ‘
0	BRq 1	BRq 1	ORq 2	—	OLq 4
1	1Rq 2	1Rq 2	1Rq 2	—	1Lq 4
В	BRq 1	BLq 3	BLq 4	OLq f	BRq f

Многоленточная машина Тьюринга

Многоленточные машины Тьюринга имеют несколько лент, к которым каждая лента доступна с отдельной головкой. Каждая голова может двигаться независимо от других голов. Первоначально вход находится на ленте 1, а остальные пустые. Сначала первая лента занята вводом, а остальные ленты остаются пустыми. Затем, машина читает последовательные символы под своими головами, и ТМ печатает символ на каждой ленте и перемещает свои головы.

Многоленточная машина Тьюринга может быть формально описана как 6-кортеж (Q, X, B, δ, q ₀ , F), где —

• Q — конечное множество состояний

• X это ленточный алфавит

• B — это пустой символ

• δ — отношение к состояниям и символам, где

  δ: Q × X ^k → Q × (X × {сдвиг влево, сдвиг вправо, сдвиг вправо}) ^k

  где есть k количество лент

• q ₀ — начальное состояние

• F — множество конечных состояний

Q — конечное множество состояний

X это ленточный алфавит

B — это пустой символ

δ — отношение к состояниям и символам, где

δ: Q × X ^k → Q × (X × {сдвиг влево, сдвиг вправо, сдвиг вправо}) ^k

где есть k количество лент

q ₀ — начальное состояние

F — множество конечных состояний

Примечание. Каждая многопленочная машина Тьюринга имеет эквивалентную одноленточную машину Тьюринга.

Многодорожечная машина Тьюринга

Многоканальные машины Тьюринга, особый тип многоканальной машины Тьюринга, содержат несколько дорожек, но только одна ленточная головка считывает и записывает все дорожки. Здесь одна головка ленты считывает n символов из n дорожек за один шаг. Он принимает рекурсивно перечислимые языки, как это допускает обычная одноленточная одноленточная машина Turing.

Многодорожечная машина Тьюринга может быть формально описана как 6-кортеж (Q, X, ∑, δ, q ₀ , F), где —

• Q — конечное множество состояний

• X это ленточный алфавит

• ∑ является входным алфавитом

• δ — отношение к состояниям и символам, где

  δ (Q _i , [a ₁ , a ₂ , a ₃ , ….]) = (Q _j , [b ₁ , b ₂ , b ₃ , ….], Left_shift или Right_shift)

• q ₀ — начальное состояние

• F — множество конечных состояний

Q — конечное множество состояний

X это ленточный алфавит

∑ является входным алфавитом

δ — отношение к состояниям и символам, где

δ (Q _i , [a ₁ , a ₂ , a ₃ , ….]) = (Q _j , [b ₁ , b ₂ , b ₃ , ….], Left_shift или Right_shift)

q ₀ — начальное состояние

F — множество конечных состояний

Примечание. Для каждой машины Тьюринга S с одной дорожкой существует эквивалентная машина Тьюринга с несколькими дорожками, такая, что L (S) = L (M) .

Недетерминированная машина Тьюринга

В недетерминированной машине Тьюринга для каждого состояния и символа существует группа действий, которые может выполнять ТМ. Итак, здесь переходы не являются детерминированными. Вычисление недетерминированной машины Тьюринга представляет собой дерево конфигураций, к которым можно получить доступ из начальной конфигурации.

Вход принимается, если есть хотя бы один узел дерева, который является конфигурацией принятия, в противном случае он не принимается. Если все ветви вычислительного дерева останавливаются на всех входах, недетерминированная машина Тьюринга называется Decider, и если для некоторого ввода все ветви отклоняются, вход также отклоняется.

Недетерминированная машина Тьюринга может быть формально определена как 6-кортеж (Q, X, ∑, δ, q ₀ , B, F), где —

• Q — конечное множество состояний

• X это ленточный алфавит

• ∑ является входным алфавитом

• δ — переходная функция;

  δ: Q × X → P (Q × X × {сдвиг влево, сдвиг вправо}).

• q ₀ — начальное состояние

• B — это пустой символ

• F — множество конечных состояний

Q — конечное множество состояний

X это ленточный алфавит

∑ является входным алфавитом

δ — переходная функция;

δ: Q × X → P (Q × X × {сдвиг влево, сдвиг вправо}).

q ₀ — начальное состояние

B — это пустой символ

F — множество конечных состояний

Полу-бесконечная лента Тьюринга

Машина Тьюринга с полубесконечной лентой имеет левый конец, но не имеет правого конца. Левый конец ограничен маркером конца.

Это двухполосная лента —

• Верхняя дорожка — представляет ячейки справа от начальной позиции головы.

• Нижняя дорожка — представляет ячейки слева от начальной позиции головы в обратном порядке.

Верхняя дорожка — представляет ячейки справа от начальной позиции головы.

Нижняя дорожка — представляет ячейки слева от начальной позиции головы в обратном порядке.

Входная строка бесконечной длины изначально записывается на ленту в непрерывных ячейках ленты.

Машина запускается из начального состояния q _0, а головка сканирует левый крайний маркер «Конец». На каждом шаге он читает символ на ленте под своей головой. Он записывает новый символ в эту ячейку ленты, а затем перемещает головку в левую или правую ячейку ленты. Функция перехода определяет действия, которые необходимо предпринять.

У него есть два специальных состояния: состояние принятия и состояние отказа . Если в любой момент времени он входит в принятое состояние, ввод принимается, и если он входит в состояние отклонения, ввод отклоняется TM. В некоторых случаях он продолжает работать бесконечно, не будучи принятым или отклоненным для некоторых определенных входных символов.

Примечание. Машины Тьюринга с полубесконечной лентой эквивалентны стандартным машинам Тьюринга.

Линейно ограниченные автоматы

Линейный ограниченный автомат является многодорожечной недетерминированной машиной Тьюринга с лентой некоторой ограниченной конечной длины.

Длина = функция (длина исходной входной строки, константа с)

Вот,

Информация о памяти ≤ c × Входная информация

Вычисление ограничено постоянной ограниченной областью. Входной алфавит содержит два специальных символа, которые служат в качестве маркеров левого конца и маркеров правого конца, что означает, что переходы не перемещаются ни влево от левого маркера конца, ни справа от правого маркера конца ленты.

Линейный ограниченный автомат может быть определен как 8-набор (Q, X, ∑, q ₀ , ML, MR, δ, F), где —

• Q — конечное множество состояний

• X это ленточный алфавит

• ∑ является входным алфавитом

• q ₀ — начальное состояние

• M _L — маркер левого конца

• M _R — маркер правого конца, где M _R ≠ M _L

• δ — это функция перехода, которая отображает каждую пару (состояние, символ ленты) в (состояние, символ ленты, константа ‘c’), где c может быть 0, +1 или -1

• F — множество конечных состояний

Q — конечное множество состояний

X это ленточный алфавит

∑ является входным алфавитом

q ₀ — начальное состояние

M _L — маркер левого конца

M _R — маркер правого конца, где M _R ≠ M _L

δ — это функция перехода, которая отображает каждую пару (состояние, символ ленты) в (состояние, символ ленты, константа ‘c’), где c может быть 0, +1 или -1

F — множество конечных состояний

Детерминированный линейный ограниченный автомат всегда чувствителен к контексту, а линейный ограниченный автомат с пустым языком неразрешим. ,

Разрешимость языка

Язык называется Decidable или Recursive, если есть машина Тьюринга, которая принимает и останавливает каждую входную строку w . Каждый решаемый язык является приемлемым по Тьюрингу.

Решение проблемы P разрешимо, если язык L всех экземпляров yes для P разрешим.

Для разрешимого языка, для каждой входной строки, TM останавливается либо в состоянии принятия, либо в состоянии отказа, как показано на следующей диаграмме —

Пример 1

Узнайте, разрешима ли следующая проблема —

Является ли число ‘m’ простым?

Решение

Простые числа = {2, 3, 5, 7, 11, 13, ………… ..}

Разделите число «m» на все числа от «2» до «√m», начиная с «2».

Если какое-либо из этих чисел выдает остаток ноль, то он переходит в «Отклоненное состояние», в противном случае он переходит в «Принятое состояние». Таким образом, здесь ответ может быть «Да» или «Нет».

Следовательно, это разрешимая проблема.

Пример 2

Учитывая регулярный язык L и строку w , как мы можем проверить, если w ∈ L ?

Решение

Возьмите DFA, который принимает L, и проверьте, принят ли w

Некоторые более решаемые проблемы —

• Принимает ли DFA пустой язык?
• Является ли L ₁ ∩ L ₂ = ∅ для регулярных множеств?

Примечание —

• Если язык L разрешим, то его дополнение L ‘ также разрешимо

• Если язык разрешим, то для него есть перечислитель.

Если язык L разрешим, то его дополнение L ‘ также разрешимо

Если язык разрешим, то для него есть перечислитель.

Неразрешимые языки

Для неразрешимого языка нет машины Тьюринга, которая принимает язык и принимает решение для каждой входной строки w (хотя TM может принять решение для некоторой входной строки). Решение проблемы P называется «неразрешимым», если язык L всех экземпляров yes для P не разрешим. Неразрешимые языки не являются рекурсивными языками, но иногда они могут быть рекурсивно перечислимыми языками.

пример

• Проблема остановки машины Тьюринга
• Проблема смертности
• Проблема смертной матрицы
• Почтовая переписка и т. Д.

Проблема остановки машины Тьюринга

Ввод — машина Тьюринга и входная строка w .

Проблема — Завершает ли машина Тьюринга вычисление строки w за конечное число шагов? Ответ должен быть либо да, либо нет.

Доказательство. Сначала мы предположим, что такая машина Тьюринга существует для решения этой проблемы, а затем покажем, что она противоречит самой себе. Мы будем называть эту машину Тьюринга остановочной машиной, которая выдает «да» или «нет» за конечное время. Если машина для остановки останавливается за конечное время, вывод будет «да», в противном случае — «нет». Ниже приведена блок-схема машины для остановки.

Теперь мы спроектируем инвертированную стопорную машину (HM) ‘ как —

• Если H возвращает YES, то цикл навсегда.

• Если H возвращает NO, тогда остановите.

Если H возвращает YES, то цикл навсегда.

Если H возвращает NO, тогда остановите.

Ниже приводится блок-схема «инвертированная Остановка машины» —

Кроме того, машина (HM) _2, сам ввод которой построен следующим образом:

• Если (HM) ₂ останавливается на входе, петля навсегда.
• Остальное, остановка

Здесь у нас есть противоречие. Следовательно, проблема остановки неразрешима .

Теорема Райса

Теорема Райса утверждает, что любое нетривиальное семантическое свойство языка, которое распознается машиной Тьюринга, неразрешимо. Свойство P — это язык всех машин Тьюринга, которые удовлетворяют этому свойству.

Формальное определение

Если P является нетривиальным свойством, а язык, содержащий свойство L _p , распознается машиной Тьюринга M, то L _p = {<M> | L (M) ∈ P} неразрешима.

Описание и свойства

• Свойство языков P — это просто набор языков. Если какой-либо язык принадлежит P (L ∈ P), говорят, что L удовлетворяет свойству P.

• Свойство называется тривиальным, если оно не удовлетворяется какими-либо рекурсивно перечислимыми языками или если оно удовлетворяется всеми рекурсивно перечислимыми языками.

• Нетривиальное свойство удовлетворяется некоторыми рекурсивно перечислимыми языками и не удовлетворяется другими. Формально говоря, в нетривиальном свойстве, где L ∈ P, выполняются оба следующих свойства:

  • Свойство 1. Существуют машины Тьюринга, M1 и M2, которые распознают один и тот же язык, т. Е. Либо (<M1>, <M2> ∈ L), либо (<M1>, <M2> ∉ L)

  • Свойство 2 — Существуют машины Тьюринга M1 и M2, где M1 распознает язык, а M2 — нет, то есть <M1> ∈ L и <M2> ∉ L

Свойство языков P — это просто набор языков. Если какой-либо язык принадлежит P (L ∈ P), говорят, что L удовлетворяет свойству P.

Свойство называется тривиальным, если оно не удовлетворяется какими-либо рекурсивно перечислимыми языками или если оно удовлетворяется всеми рекурсивно перечислимыми языками.

Нетривиальное свойство удовлетворяется некоторыми рекурсивно перечислимыми языками и не удовлетворяется другими. Формально говоря, в нетривиальном свойстве, где L ∈ P, выполняются оба следующих свойства:

Свойство 1. Существуют машины Тьюринга, M1 и M2, которые распознают один и тот же язык, т. Е. Либо (<M1>, <M2> ∈ L), либо (<M1>, <M2> ∉ L)

Свойство 2 — Существуют машины Тьюринга M1 и M2, где M1 распознает язык, а M2 — нет, то есть <M1> ∈ L и <M2> ∉ L

доказательство

Предположим, что свойство P нетривиально и φ ∈ P.

Поскольку P нетривиален, по крайней мере один язык удовлетворяет P, т. Е. L (M ₀ ) ∈ P, Machine машина Тьюринга M ₀ .

Пусть, w будет входом в конкретный момент, а N является машиной Тьюринга, которая следует

На входе х

• Беги М на ж
• Если M не принимает (или не останавливает), то не принимает x (или не останавливает)
• Если M принимает w, тогда запустите M ₀ на x. Если M ₀ принимает x, то принимает x.

Функция, которая отображает экземпляр ATM = {<M, w> | M принимает ввод w} к N так, что

• Если M принимает w и N принимает тот же язык, что и M ₀ , то L (M) = L (M ₀ ) ∈ p
• Если M не принимает w и N принимает φ, то L (N) = φ ∉ p

Поскольку _ТМ неразрешима и может быть уменьшена до Lp, Lp также неразрешима.

Проблема почтовой корреспонденции

Проблема почтовой корреспонденции (PCP), представленная Эмилем Постом в 1946 году, является неразрешимой проблемой решения. Задача PCP над алфавитом stated формулируется следующим образом:

Учитывая следующие два списка, M и N непустых строк над ∑ —

M = (x ₁ , x ₂ , x ₃ , ………, x _n )

N = (y ₁ , y ₂ , y ₃ , ………, y _n )

Можно сказать, что существует решение для почтовой корреспонденции, если для некоторого i ₁ , i ₂ , ………… i _k , где 1 ≤ i _j ≤ n, условие x _i1 …… .x _ik = y _i1 ……. у _ик удовлетворяет.

Пример 1

Найти ли списки

M = (abb, aa, aaa) и N = (bba, aaa, aa)

есть решение для почтовой корреспонденции?

Решение

	х 1	х 2	х 3
M	уток	аа	ааа
N	BBA	ааа	аа

Вот,

х ₂ х ₁ х ₃ = ‘аааббааа’

и y ₂ y ₁ y ₃ = ‘aaabbaaa’

Мы это видим

х ₂ х ₁ х ₃ = у ₂ у ₁ у ₃

Следовательно, решение i = 2, j = 1 и k = 3.

Пример 2

Найдите, имеют ли списки M = (ab, bab, bbaaa) и N = (a, ba, bab) решение для почтовой корреспонденции?

Решение

	х 1	х 2	х 3
M	аб	бабы	bbaaa
N		ба	бабы

В этом случае нет решения, потому что —

| х ₂ х ₁ х ₃ | ≠ | y ₂ y ₁ y ₃ | (Длина не одинакова)

Следовательно, можно сказать, что эта проблема почтовой корреспонденции неразрешима .