В предыдущей главе мы теперь увидели, как работает модель ARIMA и ее ограничения, заключающиеся в том, что она не может обрабатывать сезонные данные или многовариантные временные ряды, и, следовательно, были введены новые модели для включения этих функций.
Проблеск этих новых моделей дан здесь —
Векторная авторегрессия (VAR)
Это обобщенная версия модели авторегрессии для многомерных стационарных временных рядов. Характеризуется параметром «р».
Векторное скользящее среднее (VMA)
Это обобщенная версия модели скользящего среднего для многомерных стационарных временных рядов. Характеризуется параметром «q».
Скользящее среднее векторной авторегрессии (VARMA)
Это комбинация VAR и VMA и обобщенная версия модели ARMA для многомерных стационарных временных рядов. Он характеризуется параметрами «p» и «q». Подобно тому, как ARMA может действовать как модель AR, устанавливая параметр «q» в 0 и как модель MA, устанавливая параметр «p» в 0, VARMA также может действовать как модель VAR, устанавливая параметр «q» как 0 и как модель VMA, установив параметр ‘p’ в 0.
В [209]:
df_multi = df[['T', 'C6H6(GT)']] split = len(df) - int(0.2*len(df)) train_multi, test_multi = df_multi[0:split], df_multi[split:]
В [211]:
from statsmodels.tsa.statespace.varmax import VARMAX model = VARMAX(train_multi, order = (2,1)) model_fit = model.fit() c:\users\naveksha\appdata\local\programs\python\python37\lib\site-packages\statsmodels\tsa\statespace\varmax.py:152: EstimationWarning: Estimation of VARMA(p,q) models is not generically robust, due especially to identification issues. EstimationWarning) c:\users\naveksha\appdata\local\programs\python\python37\lib\site-packages\statsmodels\tsa\base\tsa_model.py:171: ValueWarning: No frequency information was provided, so inferred frequency H will be used. % freq, ValueWarning) c:\users\naveksha\appdata\local\programs\python\python37\lib\site-packages\statsmodels\base\model.py:508: ConvergenceWarning: Maximum Likelihood optimization failed to converge. Check mle_retvals "Check mle_retvals", ConvergenceWarning)
В [213]:
predictions_multi = model_fit.forecast( steps=len(test_multi)) c:\users\naveksha\appdata\local\programs\python\python37\lib\site-packages\statsmodels\tsa\base\tsa_model.py:320: FutureWarning: Creating a DatetimeIndex by passing range endpoints is deprecated. Use `pandas.date_range` instead. freq = base_index.freq) c:\users\naveksha\appdata\local\programs\python\python37\lib\site-packages\statsmodels\tsa\statespace\varmax.py:152: EstimationWarning: Estimation of VARMA(p,q) models is not generically robust, due especially to identification issues. EstimationWarning)
В [231]:
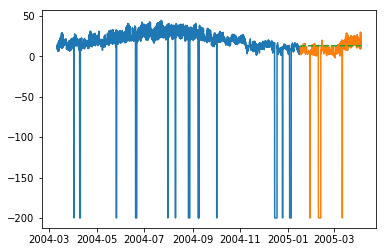
plt.plot(train_multi['T']) plt.plot(test_multi['T']) plt.plot(predictions_multi.iloc[:,0:1], '--') plt.show() plt.plot(train_multi['C6H6(GT)']) plt.plot(test_multi['C6H6(GT)']) plt.plot(predictions_multi.iloc[:,1:2], '--') plt.show()
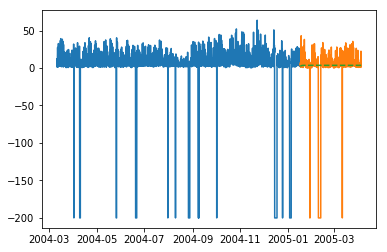
Приведенный выше код показывает, как модель VARMA может использоваться для моделирования многомерных временных рядов, хотя эта модель может не подходить для наших данных.
VARMA с экзогенными переменными (VARMAX)
Это расширение модели VARMA, где дополнительные переменные, называемые ковариатами, используются для моделирования первичной переменной, которая нас интересует.
Сезонная Авто Регрессивная Интегрированная Скользящая Средняя (SARIMA)
Это расширение модели ARIMA для работы с сезонными данными. Он делит данные на сезонные и несезонные компоненты и моделирует их аналогичным образом. Он характеризуется 7 параметрами, для параметров несезонной части (p, d, q), таких же, как для модели ARIMA, и для параметров сезонной части (P, D, Q, m), где «m» — число сезонных периодов и P, D, Q аналогичны параметрам модели ARIMA. Эти параметры могут быть откалиброваны с использованием сетки поиска или генетического алгоритма.
SARIMA с экзогенными переменными (SARIMAX)
Это расширение модели SARIMA для включения экзогенных переменных, которые помогают нам моделировать интересующую нас переменную.
Может быть полезно провести анализ взаимосвязи переменных, прежде чем ставить их в качестве экзогенных переменных.
В [251]:
from scipy.stats.stats import pearsonr
x = train_multi['T'].values
y = train_multi['C6H6(GT)'].values
corr , p = pearsonr(x,y)
print ('Corelation Coefficient =', corr,'\nP-Value =',p)
Corelation Coefficient = 0.9701173437269858
P-Value = 0.0
Корреляция Пирсона показывает линейную зависимость между двумя переменными, чтобы интерпретировать результаты, мы сначала посмотрим на значение р, если оно меньше 0,05, то значение коэффициента является значимым, иначе значение коэффициента не является значимым. Для значимого p-значения положительное значение коэффициента корреляции указывает на положительную корреляцию, а отрицательное значение указывает на отрицательную корреляцию.
Следовательно, по нашим данным, «температура» и «C6H6», по-видимому, имеют очень положительную корреляцию. Поэтому мы будем
В [297]:
from statsmodels.tsa.statespace.sarimax import SARIMAX model = SARIMAX(x, exog = y, order = (2, 0, 2), seasonal_order = (2, 0, 1, 1), enforce_stationarity=False, enforce_invertibility = False) model_fit = model.fit(disp = False) c:\users\naveksha\appdata\local\programs\python\python37\lib\site-packages\statsmodels\base\model.py:508: ConvergenceWarning: Maximum Likelihood optimization failed to converge. Check mle_retvals "Check mle_retvals", ConvergenceWarning)
В [298]:
y_ = test_multi['C6H6(GT)'].values predicted = model_fit.predict(exog=y_) test_multi_ = pandas.DataFrame(test) test_multi_['predictions'] = predicted[0:1871]
В [299]:
plt.plot(train_multi['T']) plt.plot(test_multi_['T']) plt.plot(test_multi_.predictions, '--')
Из [299]:
[<matplotlib.lines.Line2D at 0x1eab0191c18>]
Прогнозы здесь, кажется, принимают большие вариации в отличие от одномерного моделирования ARIMA.
Само собой разумеется, SARIMAX может использоваться как модель ARX, MAX, ARMAX или ARIMAX, устанавливая только соответствующие параметры в ненулевые значения.
Дробная авторегрессивная интегрированная скользящая средняя (FARIMA)
Иногда может случиться, что наш ряд не является стационарным, но различие с параметром ‘d’, принимающим значение 1, может привести к его чрезмерной разнице. Таким образом, нам нужно различать временные ряды, используя дробное значение.
В мире науки о данных нет единой превосходящей модели, модель, которая работает с вашими данными, сильно зависит от вашего набора данных. Знание различных моделей позволяет нам выбирать модель, которая работает с нашими данными и экспериментирует с этой моделью для достижения наилучших результатов. И результаты должны рассматриваться как график, а также метрики ошибок, иногда небольшая ошибка также может быть плохой, следовательно, построение графика и визуализация результатов очень важны.
В следующей главе мы рассмотрим другую статистическую модель — экспоненциальное сглаживание.