Временные ряды — Введение

Временной ряд — это последовательность наблюдений за определенный период. Одномерный временной ряд состоит из значений, взятых одной переменной в периодических экземплярах времени за период, а многомерный временной ряд состоит из значений, взятых несколькими переменными в одном и том же периодическом времени за период. Простейшим примером временного ряда, с которым мы все сталкиваемся ежедневно, является изменение температуры в течение дня, недели, месяца или года.

Анализ временных данных способен дать нам полезную информацию о том, как переменная изменяется во времени или как она зависит от изменения значений другой переменной (ей). Это отношение переменной к ее предыдущим значениям и / или другим переменным может быть проанализировано для прогнозирования временных рядов и имеет многочисленные применения в искусственном интеллекте.

Временной ряд — Языки программирования

Базовое понимание любого языка программирования важно для пользователя, чтобы работать или развивать проблемы машинного обучения. Список предпочтительных языков программирования для тех, кто хочет работать над машинным обучением, приведен ниже —

питон

Это интерпретируемый язык программирования высокого уровня, быстрый и простой в коде. Python может следовать парадигмам процедурного или объектно-ориентированного программирования. Наличие множества библиотек упрощает реализацию сложных процедур. В этом уроке мы будем кодировать на Python, а соответствующие библиотеки, полезные для моделирования временных рядов, будут обсуждаться в следующих главах.

р

Подобно Python, R представляет собой интерпретируемый мультипарадигмальный язык, который поддерживает статистические вычисления и графику. Разнообразие пакетов облегчает реализацию моделирования машинного обучения в R.

Джава

Это интерпретируемый объектно-ориентированный язык программирования, широко известный широким спектром доступности пакетов и сложными методами визуализации данных.

C / C ++

Это скомпилированные языки и два самых старых языка программирования. Эти языки часто предпочитают включать возможности ML в уже существующие приложения, поскольку они позволяют легко настраивать реализацию алгоритмов ML.

MATLAB

MATrix LAB Laboratory — это мультипарадигмальный язык, обеспечивающий работу с матрицами. Это позволяет математические операции для сложных задач. Он в основном используется для числовых операций, но некоторые пакеты также допускают графическое многодоменное моделирование и проектирование на основе моделей.

Другие предпочтительные языки программирования для задач машинного обучения включают JavaScript, LISP, Prolog, SQL, Scala, Julia, SAS и т. Д.

Временной ряд — библиотеки Python

Python пользуется заслуженной популярностью среди тех, кто занимается машинным обучением, благодаря своей простой в написании и понятной структуре кода, а также широкому выбору библиотек с открытым исходным кодом. Несколько таких библиотек с открытым исходным кодом, которые мы будем использовать в следующих главах, были представлены ниже.

NumPy

Числовой Python — это библиотека, используемая для научных вычислений. Он работает с N-мерным объектом массива и предоставляет базовые математические функции, такие как размер, форма, среднее значение, стандартное отклонение, минимум, максимум, а также некоторые более сложные функции, такие как линейные алгебраические функции и преобразование Фурье. Вы узнаете больше об этом по мере продвижения в этом уроке.

Панды

Эта библиотека предоставляет высокоэффективные и простые в использовании структуры данных, такие как серии, кадры данных и панели. Он расширил функциональность Python от простого сбора и подготовки данных до анализа данных. Две библиотеки, Pandas и NumPy, делают любую операцию с маленьким или очень большим набором данных очень простой. Чтобы узнать больше об этих функциях, следуйте этому руководству.

SciPy

Science Python — это библиотека, используемая для научных и технических вычислений. Он предоставляет функции для оптимизации, обработки сигналов и изображений, интеграции, интерполяции и линейной алгебры. Эта библиотека пригодится при выполнении машинного обучения. Мы обсудим эти функции по мере продвижения в этом уроке.

Scikit Learn

Эта библиотека представляет собой SciPy Toolkit, широко используемый для статистического моделирования, машинного обучения и глубокого обучения, поскольку содержит различные настраиваемые модели регрессии, классификации и кластеризации. Он хорошо работает с Numpy, Pandas и другими библиотеками, что облегчает его использование.

Statsmodels

Как и Scikit Learn, эта библиотека используется для статистического исследования данных и статистического моделирования. Он также хорошо работает с другими библиотеками Python.

Matplotlib

Эта библиотека используется для визуализации данных в различных форматах, таких как линейный график, гистограмма, тепловые карты, диаграммы рассеяния, гистограмма и т. Д. Она содержит все функции, связанные с графиком, необходимые от построения графика до маркировки. Мы обсудим эти функции по мере продвижения в этом уроке.

Эти библиотеки очень важны для начала машинного обучения с любыми данными.

Помимо обсуждавшихся выше, еще одна библиотека, особенно важная для работы с временными рядами, — это

Datetime

Эта библиотека с двумя модулями — datetime и calendar — предоставляет все необходимые функции datetime для чтения, форматирования и управления временем.

Мы будем использовать эти библиотеки в следующих главах.

Временной ряд — обработка данных и визуализация

Временной ряд — это последовательность наблюдений, проиндексированных в равных интервалах времени. Следовательно, порядок и непрерывность должны поддерживаться в любом временном ряду.

Набор данных, который мы будем использовать, представляет собой многовариантный временной ряд, содержащий почасовые данные в течение приблизительно одного года, для качества воздуха в сильно загрязненном итальянском городе. Набор данных можно скачать по приведенной ниже ссылке — https://archive.ics.uci.edu/ml/datasets/air+quality .

Необходимо убедиться, что —

• Временные ряды расположены на одинаковом расстоянии, и

• В нем нет избыточных значений или пробелов.

Временные ряды расположены на одинаковом расстоянии, и

В нем нет избыточных значений или пробелов.

Если временной ряд не является непрерывным, мы можем увеличить или уменьшить его.

Отображение df.head ()

В [122]:

import pandas

В [123]:

df = pandas.read_csv("AirQualityUCI.csv", sep = ";", decimal = ",")
df = df.iloc[ : , 0:14]

В [124]:

len(df)

Из [124]:

9471

В [125]:

df.head()

Из [125]:

Для предварительной обработки временного ряда мы должны убедиться, что в наборе данных нет значений NaN (NULL); если они есть, мы можем заменить их либо на 0, либо на среднее, либо на предшествующее или последующее значение. Замена является предпочтительным выбором по сравнению с отбрасыванием, чтобы сохранить непрерывность временных рядов. Однако в нашем наборе данных последние несколько значений кажутся NULL и, следовательно, отбрасывание не повлияет на непрерывность.

Отбрасывание NaN (не число)

В [126]:

df.isna().sum()
Out[126]:
Date             114
Time             114
CO(GT)           114
PT08.S1(CO)      114
NMHC(GT)         114
C6H6(GT)         114
PT08.S2(NMHC)    114
NOx(GT)          114
PT08.S3(NOx)     114
NO2(GT)          114
PT08.S4(NO2)     114
PT08.S5(O3)      114
T                114
RH               114
dtype: int64

В [127]:

df = df[df['Date'].notnull()]

В [128]:

df.isna().sum()

Из [128]:

Date             0
Time             0
CO(GT)           0
PT08.S1(CO)      0
NMHC(GT)         0
C6H6(GT)         0
PT08.S2(NMHC)    0
NOx(GT)          0
PT08.S3(NOx)     0
NO2(GT)          0
PT08.S4(NO2)     0
PT08.S5(O3)      0
T                0
RH               0
dtype: int64

Временные ряды обычно изображаются в виде линейных графиков в зависимости от времени. Для этого мы теперь скомбинируем столбец даты и времени и преобразуем его в объект datetime из строк. Это может быть выполнено с использованием библиотеки datetime.

Преобразование в объект даты и времени

В [129]:

df['DateTime'] = (df.Date) + ' ' + (df.Time)
print (type(df.DateTime[0]))

<класс ‘str’>

В [130]:

import datetime

df.DateTime = df.DateTime.apply(lambda x: datetime.datetime.strptime(x, '%d/%m/%Y %H.%M.%S'))
print (type(df.DateTime[0]))

<class ‘pandas._libs.tslibs.timestamps.Timestamp’>

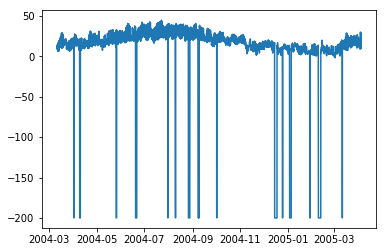
Давайте посмотрим, как некоторые переменные, такие как температура, меняются во времени.

Отображение графиков

В [131]:

df.index = df.DateTime

В [132]:

import matplotlib.pyplot as plt
plt.plot(df['T'])

Из [132]:

[<matplotlib.lines.Line2D at 0x1eaad67f780>]

В [208]:

plt.plot(df['C6H6(GT)'])

Из [208]:

[<matplotlib.lines.Line2D at 0x1eaaeedff28>]

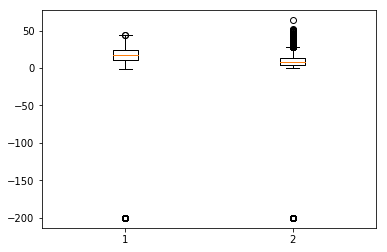
Боксовые диаграммы — это еще один полезный вид графиков, который позволяет вам собирать много информации о наборе данных в один график. Он показывает среднее значение, 25% и 75% квартиль и выбросы одной или нескольких переменных. В случае, когда число выбросов мало и очень далеко от среднего, мы можем устранить выбросы, установив для них среднее значение или значение квартиля 75%.

Показ Boxplots

В [134]:

plt.boxplot(df[['T','C6H6(GT)']].values)

Из [134]:

{'whiskers': [<matplotlib.lines.Line2D at 0x1eaac16de80>,
   <matplotlib.lines.Line2D at 0x1eaac16d908>,
   <matplotlib.lines.Line2D at 0x1eaac177a58>,
   <matplotlib.lines.Line2D at 0x1eaac177cf8>],
   'caps': [<matplotlib.lines.Line2D at 0x1eaac16d2b0>,
   <matplotlib.lines.Line2D at 0x1eaac16d588>,
   <matplotlib.lines.Line2D at 0x1eaac1a69e8>,
   <matplotlib.lines.Line2D at 0x1eaac1a64a8>],
   'boxes': [<matplotlib.lines.Line2D at 0x1eaac16dc50>,
   <matplotlib.lines.Line2D at 0x1eaac1779b0>],
   'medians': [<matplotlib.lines.Line2D at 0x1eaac16d4a8>,
   <matplotlib.lines.Line2D at 0x1eaac1a6c50>],
   'fliers': [<matplotlib.lines.Line2D at 0x1eaac177dd8>,
   <matplotlib.lines.Line2D at 0x1eaac1a6c18>],'means': []
}

Временные ряды — Моделирование

Вступление

Временной ряд состоит из 4 компонентов, как указано ниже —

• Уровень — это среднее значение, вокруг которого изменяется ряд.

• Тренд. Поведение переменной в зависимости от времени.

• Сезонность — это циклическое поведение временных рядов.

• Шум — это ошибка в наблюдениях, добавленная из-за факторов окружающей среды.

Уровень — это среднее значение, вокруг которого изменяется ряд.

Тренд. Поведение переменной в зависимости от времени.

Сезонность — это циклическое поведение временных рядов.

Шум — это ошибка в наблюдениях, добавленная из-за факторов окружающей среды.

Методы моделирования временных рядов

Для захвата этих компонентов существует ряд популярных методов моделирования временных рядов. В этом разделе дается краткое введение в каждую технику, однако мы подробно обсудим их в следующих главах.

Наивные методы

Это простые методы оценки, например, прогнозируемому значению присваивается значение, равное среднему значению предшествующих значений зависимой от времени переменной или предыдущего фактического значения. Они используются для сравнения со сложными методами моделирования.

Авто Регрессия

Авторегрессия прогнозирует значения будущих периодов времени в зависимости от значений предыдущих периодов времени. Прогнозы авторегрессии могут лучше соответствовать данным, чем наивные методы, но они могут не учитывать сезонность.

ARIMA Модель

Авторегрессионное интегрированное скользящее среднее моделирует значение переменной как линейную функцию от предыдущих значений и остаточных ошибок на предыдущих временных шагах стационарных временных рядов. Однако данные реального мира могут быть нестационарными и иметь сезонность, поэтому были разработаны Seasonal-ARIMA и Fractional-ARIMA. ARIMA работает с одномерными временными рядами, для обработки нескольких переменных была введена VARIMA.

Экспоненциальное сглаживание

Он моделирует значение переменной как экспоненциально взвешенную линейную функцию предыдущих значений. Эта статистическая модель может также учитывать тенденции и сезонность.

LSTM

Модель долговременной кратковременной памяти (LSTM) — это рекуррентная нейронная сеть, которая используется для временных рядов для учета долгосрочных зависимостей. Он может быть обучен с большим количеством данных, чтобы уловить тенденции во множественных временных рядах.

Указанные методы моделирования используются для регрессии временных рядов. В следующих главах давайте теперь рассмотрим все это один за другим.

Временной ряд — калибровка параметров

Вступление

Любая статистическая или машинная модель обучения имеет некоторые параметры, которые сильно влияют на то, как моделируются данные. Например, ARIMA имеет значения p, d, q. Эти параметры должны быть определены так, чтобы ошибка между фактическими значениями и смоделированными значениями была минимальной. Калибровка параметров считается наиболее важной и трудоемкой задачей подбора модели. Следовательно, для нас очень важно выбрать оптимальные параметры.

Методы калибровки параметров

Существуют различные способы калибровки параметров. В этом разделе подробно рассказывается о некоторых из них.

Хит-и-попробовать

Одним из распространенных способов калибровки моделей является ручная калибровка, когда вы начинаете с визуализации временных рядов и интуитивно пробуете некоторые значения параметров и меняете их снова и снова, пока не достигнете достаточного соответствия. Это требует хорошего понимания модели, которую мы пробуем. Для модели ARIMA ручная калибровка выполняется с помощью графика автокорреляции для параметра «p», графика частичной автокорреляции для параметра «q» и теста ADF для подтверждения стационарности временных рядов и установки параметра «d» , Мы обсудим все это подробно в следующих главах.

Grid Search

Другой способ калибровки моделей — это поиск по сетке, что по сути означает, что вы пытаетесь построить модель для всех возможных комбинаций параметров и выбрать модель с минимальной ошибкой. Это отнимает много времени и, следовательно, полезно, когда число параметров, подлежащих калибровке, и диапазон значений, которые они принимают, меньше, поскольку это включает в себя несколько вложенных циклов.

Генетический алгоритм

Генетический алгоритм работает на биологическом принципе, что хорошее решение в конечном итоге превратится в самое «оптимальное» решение. Он использует биологические операции мутации, кроссинговера и отбора, чтобы в итоге достичь оптимального решения.

Для получения дополнительных знаний вы можете прочитать о других методах оптимизации параметров, таких как байесовская оптимизация и оптимизация Swarm.

Временной ряд — наивные методы

Вступление

Наивные методы, такие как предположение, что прогнозируемое значение в момент времени «t» является фактическим значением переменной в момент времени «t-1» или скользящего среднего значения ряда, используются для оценки того, насколько хорошо могут работать статистические модели и модели машинного обучения. и подчеркнуть их необходимость.

В этой главе давайте попробуем эти модели на одной из особенностей наших данных временных рядов.

Сначала мы увидим среднее значение «температуры» наших данных и отклонение вокруг них. Также полезно видеть максимальные и минимальные значения температуры. Мы можем использовать функциональные возможности библиотеки numpy здесь.

Отображение статистики

В [135]:

import numpy
print (
   'Mean: ',numpy.mean(df['T']), '; 
   Standard Deviation: ',numpy.std(df['T']),'; 
   \nMaximum Temperature: ',max(df['T']),'; 
   Minimum Temperature: ',min(df['T'])
)

У нас есть статистика для всех 9357 наблюдений на равноправной временной шкале, которая полезна для понимания данных.

Теперь мы попробуем первый наивный метод, установив прогнозируемое значение в настоящее время равным фактическому значению в предыдущий раз, и рассчитаем среднеквадратичную ошибку (RMSE) для него, чтобы количественно оценить эффективность этого метода.

Показ 1- ^го наивного метода

В [136]:

df['T']
df['T_t-1'] = df['T'].shift(1)

В [137]:

df_naive = df[['T','T_t-1']][1:]

В [138]:

from sklearn import metrics
from math import sqrt

true = df_naive['T']
prediction = df_naive['T_t-1']
error = sqrt(metrics.mean_squared_error(true,prediction))
print ('RMSE for Naive Method 1: ', error)

СКО для наивного метода 1: 12,901140576492974

Давайте посмотрим на следующий наивный метод, где прогнозируемое значение в настоящее время приравнивается к среднему значению периодов времени, предшествующих ему. Мы рассчитаем RMSE для этого метода тоже.

Показ 2- ^го наивного метода

В [139]:

df['T_rm'] = df['T'].rolling(3).mean().shift(1)
df_naive = df[['T','T_rm']].dropna()

В [140]:

true = df_naive['T']
prediction = df_naive['T_rm']
error = sqrt(metrics.mean_squared_error(true,prediction))
print ('RMSE for Naive Method 2: ', error)

СКО для наивного метода 2: 14.957633272839242

Здесь вы можете поэкспериментировать с различным количеством предыдущих периодов времени, которые также называются «лагами», которые вы хотите учесть, и здесь они равны 3. По этим данным видно, что по мере увеличения количества лагов и ошибок увеличивается. Если задержка сохраняется равной 1, она становится такой же, как ранее использовавшийся наивный метод.

Указывает на заметку

• Вы можете написать очень простую функцию для вычисления среднеквадратичной ошибки. Здесь мы использовали функцию среднего квадрата ошибки из пакета ‘sklearn’, а затем взяли ее квадратный корень.

• В pandas df [‘column_name’] также может быть записано как df.column_name, однако для этого набора данных df.T не будет работать так же, как df [‘T’], потому что df.T — это функция для транспонирования кадра данных. Поэтому используйте только df [‘T’] или рассмотрите возможность переименования этого столбца перед использованием другого синтаксиса.

Вы можете написать очень простую функцию для вычисления среднеквадратичной ошибки. Здесь мы использовали функцию среднего квадрата ошибки из пакета ‘sklearn’, а затем взяли ее квадратный корень.

В pandas df [‘column_name’] также может быть записано как df.column_name, однако для этого набора данных df.T не будет работать так же, как df [‘T’], потому что df.T — это функция для транспонирования кадра данных. Поэтому используйте только df [‘T’] или рассмотрите возможность переименования этого столбца перед использованием другого синтаксиса.

Временной ряд — авторегрессия

Для стационарного временного ряда модели авторегрессии видят значение переменной в момент времени «t» как линейную функцию от значений «p» временных шагов, предшествующих ему. Математически это можно записать как —

yt=C+ phi1yt−1+ phi2Yt−2+...+ phipyф+ epsilonт

$$y_ {t} = \: C + \: \ phi_ {1} y_ {t-1} \: + \: \ phi_ {2} Y_ {t-2} + ... + \ phi_ {p} y_ {ф} + \ epsilon_ {т}$$

Где ‘p’ — параметр авторегрессивного тренда

 epsilont$\ epsilon_ {t}$ — это белый шум, и

yt−1,yt−2...ytp$y_ {t-1}, y_ {t-2} \: \: ... y_ {tp}$ обозначают значение переменной в предыдущие периоды времени.

Значение p может быть откалибровано с использованием различных методов. Один из способов найти подходящее значение ‘p’ — построить график автокорреляции.

Примечание. Мы должны разделить данные на обучающие и протестировать их в соотношении 8: 2 к общему объему имеющихся данных, прежде чем проводить какой-либо анализ этих данных, поскольку данные тестирования предназначены только для определения точности нашей модели, а допущение о том, что они недоступны для до тех пор, пока не будут сделаны прогнозы. В случае временных рядов последовательность точек данных очень важна, поэтому следует помнить, чтобы не потерять порядок при разделении данных.

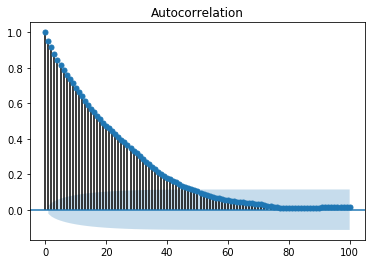
График автокорреляции или коррелограмма показывает отношение переменной к себе на предыдущих временных шагах. Он использует корреляцию Пирсона и показывает корреляции в пределах 95% доверительного интервала. Давайте посмотрим, как это выглядит для переменной температуры наших данных.

Показ ACP

В [141]:

split = len(df) - int(0.2*len(df))
train, test = df['T'][0:split], df['T'][split:]

В [142]:

from statsmodels.graphics.tsaplots import plot_acf

plot_acf(train, lags = 100)
plt.show()

Предполагается, что все значения запаздывания, лежащие за пределами затененной синей области, имеют корреляцию.

Временной ряд — скользящее среднее

Для стационарного временного ряда модель скользящего среднего рассматривает значение переменной в момент времени «t» как линейную функцию от остаточных ошибок от шагов времени «q», предшествующих ей. Остаточная ошибка рассчитывается путем сравнения значения в момент времени «t» со скользящим средним из предыдущих значений.

Математически это можно записать как —

yt=c+ epsilont+ theta1 epsilont−1+ theta2 epsilonт−2 +...+: thetaд epsilonTQ 

$$y_ {t} = c \: + \: \ epsilon_ {t} \: + \: \ theta_ {1} \: \ epsilon_ {t-1} \: + \: \ theta_ {2} \: \ epsilon_ {т-2} \ + \: ... +: \ theta_ {д} \: \ epsilon_ {TQ} \ $$

Где «q» — параметр тренда скользящего среднего

 epsilont$\ epsilon_ {t}$ — это белый шум, и

 epsilont−1, epsilont−2... epsilontq$\ epsilon_ {t-1}, \ epsilon_ {t-2} ... \ epsilon_ {tq}$ — это условия ошибки в предыдущие периоды времени.

Значение «q» можно калибровать различными способами. Один из способов найти подходящее значение «q» — построить график частичной автокорреляции.

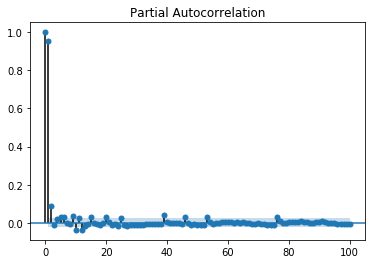
График частичной автокорреляции показывает отношение переменной к себе на предыдущих этапах времени с удаленными косвенными корреляциями, в отличие от графика автокорреляции, который показывает как прямые, так и косвенные корреляции, давайте посмотрим, как она выглядит для переменной «температура» нашего данные.

Показ PACP

В [143]:

from statsmodels.graphics.tsaplots import plot_pacf

plot_pacf(train, lags = 100)
plt.show()

Частичная автокорреляция читается так же, как коррелограмма.

Временной ряд — АРИМА

Мы уже поняли, что для стационарного временного ряда переменная в момент времени t является линейной функцией предыдущих наблюдений или остаточных ошибок. Следовательно, пришло время объединить их и получить модель авторегрессивного скользящего среднего (ARMA).

Однако временные ряды временами не являются стационарными, т. Е. Статистические свойства ряда, такие как среднее значение, изменяются во времени. И статистические модели, которые мы изучили до сих пор, предполагают, что временные ряды являются стационарными, поэтому мы можем включить этап предварительной обработки для дифференцирования временных рядов, чтобы сделать его стационарным. Теперь для нас важно выяснить, является ли временной ряд, с которым мы имеем дело, стационарным или нет.

Различные методы определения стационарности временного ряда: поиск сезонности или тренда на графике временных рядов, проверка разницы в среднем и дисперсии для разных временных периодов, расширенный критерий Дики-Фуллера (ADF), тест KPSS, показатель Херста и т. Д. ,

Давайте посмотрим, является ли переменная «температура» нашего набора данных стационарным временным рядом или нет с использованием теста ADF.

В [74]:

from statsmodels.tsa.stattools import adfuller

result = adfuller(train)
print('ADF Statistic: %f' % result[0])
print('p-value: %f' % result[1])
print('Critical Values:')
for key, value In result[4].items()
   print('\t%s: %.3f' % (key, value))

Статистика ADF: -10.406056

р-значение: 0,000000

Критические ценности:

1%: -3,431

5%: -2,862

10%: -2,567

Теперь, когда мы запустили тест ADF, давайте интерпретируем результат. Сначала мы сравним статистику АПД с критическими значениями, более низкое критическое значение говорит нам, что ряд, скорее всего, нестационарный. Далее мы видим р-значение. Значение р, превышающее 0,05, также предполагает, что временной ряд нестационарный.

В качестве альтернативы, p-значение меньше или равно 0,05 или ADF-статистика меньше критических значений предполагают, что временной ряд является стационарным.

Следовательно, временные ряды, с которыми мы имеем дело, уже стационарны. В случае стационарных временных рядов мы устанавливаем параметр ‘d’ в 0.

Мы также можем подтвердить стационарность временных рядов, используя показатель Херста.

В [75]:

import hurst

H, c,data = hurst.compute_Hc(train)
print("H = {:.4f}, c = {:.4f}".format(H,c))

H = 0,1660, с = 5,0740

Значение H <0,5 показывает антипостоянное поведение, а H> 0,5 показывает постоянное поведение или ряд трендов. H = 0.5 показывает случайное блуждание / броуновское движение. Значение Н <0,5, подтверждающее, что наша серия является стационарной.

Для нестационарного временного ряда мы устанавливаем параметр «d» равным 1. Кроме того, значение параметра авторегрессивного тренда «p» и параметра тренда скользящей средней «q» рассчитывается для стационарного временного ряда, т.е. путем построения графика ACP и PACP после различия временных рядов.

Модель ARIMA, которая характеризуется 3-мя параметрами (p, d, q), теперь нам понятна, поэтому давайте смоделируем наш временной ряд и прогнозируем будущие значения температуры.

В [156]:

from statsmodels.tsa.arima_model import ARIMA

model = ARIMA(train.values, order=(5, 0, 2))
model_fit = model.fit(disp=False)

В [157]:

predictions = model_fit.predict(len(test))
test_ = pandas.DataFrame(test)
test_['predictions'] = predictions[0:1871]

В [158]:

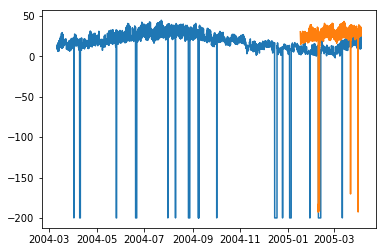
plt.plot(df['T'])
plt.plot(test_.predictions)
plt.show()

В [167]:

error = sqrt(metrics.mean_squared_error(test.values,predictions[0:1871]))
print ('Test RMSE for ARIMA: ', error)

Тест RMSE для ARIMA: 43.21252940234892

Временной ряд — вариации ARIMA

В предыдущей главе мы теперь увидели, как работает модель ARIMA и ее ограничения, заключающиеся в том, что она не может обрабатывать сезонные данные или многовариантные временные ряды, и, следовательно, были введены новые модели для включения этих функций.

Проблеск этих новых моделей дан здесь —

Векторная авторегрессия (VAR)

Это обобщенная версия модели авторегрессии для многомерных стационарных временных рядов. Характеризуется параметром «р».

Векторное скользящее среднее (VMA)

Это обобщенная версия модели скользящего среднего для многомерных стационарных временных рядов. Характеризуется параметром «q».

Скользящее среднее векторной авторегрессии (VARMA)

Это комбинация VAR и VMA и обобщенная версия модели ARMA для многомерных стационарных временных рядов. Он характеризуется параметрами «p» и «q». Подобно тому, как ARMA может действовать как модель AR, устанавливая параметр «q» в 0 и как модель MA, устанавливая параметр «p» в 0, VARMA также может действовать как модель VAR, устанавливая параметр «q» как 0 и как модель VMA, установив параметр ‘p’ в 0.

В [209]:

df_multi = df[['T', 'C6H6(GT)']]
split = len(df) - int(0.2*len(df))
train_multi, test_multi = df_multi[0:split], df_multi[split:]

В [211]:

from statsmodels.tsa.statespace.varmax import VARMAX

model = VARMAX(train_multi, order = (2,1))
model_fit = model.fit()
c:\users\naveksha\appdata\local\programs\python\python37\lib\site-packages\statsmodels\tsa\statespace\varmax.py:152: 
   EstimationWarning: Estimation of VARMA(p,q) models is not generically robust, 
   due especially to identification issues. 
   EstimationWarning)
c:\users\naveksha\appdata\local\programs\python\python37\lib\site-packages\statsmodels\tsa\base\tsa_model.py:171: 
   ValueWarning: No frequency information was provided, so inferred frequency H will be used. 
  % freq, ValueWarning)
c:\users\naveksha\appdata\local\programs\python\python37\lib\site-packages\statsmodels\base\model.py:508: 
   ConvergenceWarning: Maximum Likelihood optimization failed to converge. Check mle_retvals 
  "Check mle_retvals", ConvergenceWarning)

В [213]:

predictions_multi = model_fit.forecast( steps=len(test_multi))
c:\users\naveksha\appdata\local\programs\python\python37\lib\site-packages\statsmodels\tsa\base\tsa_model.py:320: 
   FutureWarning: Creating a DatetimeIndex by passing range endpoints is deprecated.  Use `pandas.date_range` instead.
   freq = base_index.freq)
c:\users\naveksha\appdata\local\programs\python\python37\lib\site-packages\statsmodels\tsa\statespace\varmax.py:152: 
   EstimationWarning: Estimation of VARMA(p,q) models is not generically robust, due especially to identification issues.
   EstimationWarning)

В [231]:

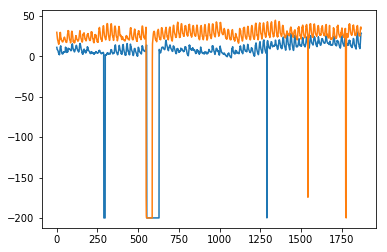
plt.plot(train_multi['T'])
plt.plot(test_multi['T'])
plt.plot(predictions_multi.iloc[:,0:1], '--')
plt.show()

plt.plot(train_multi['C6H6(GT)'])
plt.plot(test_multi['C6H6(GT)'])
plt.plot(predictions_multi.iloc[:,1:2], '--')
plt.show()

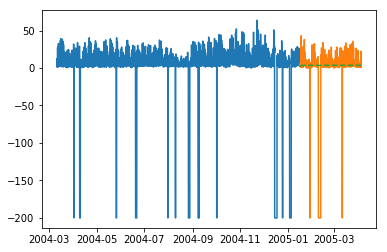
Приведенный выше код показывает, как модель VARMA может использоваться для моделирования многомерных временных рядов, хотя эта модель может не подходить для наших данных.

VARMA с экзогенными переменными (VARMAX)

Это расширение модели VARMA, где дополнительные переменные, называемые ковариатами, используются для моделирования первичной переменной, которая нас интересует.

Сезонная Авто Регрессивная Интегрированная Скользящая Средняя (SARIMA)

Это расширение модели ARIMA для работы с сезонными данными. Он делит данные на сезонные и несезонные компоненты и моделирует их аналогичным образом. Он характеризуется 7 параметрами, для параметров несезонной части (p, d, q), таких же, как для модели ARIMA, и для параметров сезонной части (P, D, Q, m), где «m» — число сезонных периодов и P, D, Q аналогичны параметрам модели ARIMA. Эти параметры могут быть откалиброваны с использованием сетки поиска или генетического алгоритма.

SARIMA с экзогенными переменными (SARIMAX)

Это расширение модели SARIMA для включения экзогенных переменных, которые помогают нам моделировать интересующую нас переменную.

Может быть полезно провести анализ взаимосвязи переменных, прежде чем ставить их в качестве экзогенных переменных.

В [251]:

from scipy.stats.stats import pearsonr
x = train_multi['T'].values
y = train_multi['C6H6(GT)'].values

corr , p = pearsonr(x,y)
print ('Corelation Coefficient =', corr,'\nP-Value =',p)
Corelation Coefficient = 0.9701173437269858
P-Value = 0.0

Корреляция Пирсона показывает линейную зависимость между двумя переменными, чтобы интерпретировать результаты, мы сначала посмотрим на значение р, если оно меньше 0,05, то значение коэффициента является значимым, иначе значение коэффициента не является значимым. Для значимого p-значения положительное значение коэффициента корреляции указывает на положительную корреляцию, а отрицательное значение указывает на отрицательную корреляцию.

Следовательно, по нашим данным, «температура» и «C6H6», по-видимому, имеют очень положительную корреляцию. Поэтому мы будем

В [297]:

from statsmodels.tsa.statespace.sarimax import SARIMAX

model = SARIMAX(x, exog = y, order = (2, 0, 2), seasonal_order = (2, 0, 1, 1), enforce_stationarity=False, enforce_invertibility = False)
model_fit = model.fit(disp = False)
c:\users\naveksha\appdata\local\programs\python\python37\lib\site-packages\statsmodels\base\model.py:508: 
   ConvergenceWarning: Maximum Likelihood optimization failed to converge. Check mle_retvals
   "Check mle_retvals", ConvergenceWarning)

В [298]:

y_ = test_multi['C6H6(GT)'].values
predicted = model_fit.predict(exog=y_)
test_multi_ = pandas.DataFrame(test)
test_multi_['predictions'] = predicted[0:1871]

В [299]:

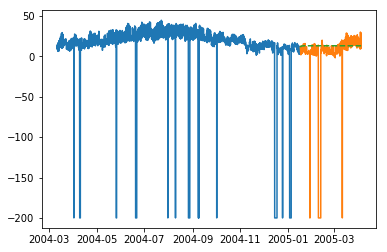
plt.plot(train_multi['T'])
plt.plot(test_multi_['T'])
plt.plot(test_multi_.predictions, '--')

Из [299]:

[<matplotlib.lines.Line2D at 0x1eab0191c18>]

Прогнозы здесь, кажется, принимают большие вариации в отличие от одномерного моделирования ARIMA.

Само собой разумеется, SARIMAX может использоваться как модель ARX, MAX, ARMAX или ARIMAX, устанавливая только соответствующие параметры в ненулевые значения.

Дробная авторегрессивная интегрированная скользящая средняя (FARIMA)

Иногда может случиться, что наш ряд не является стационарным, но различие с параметром ‘d’, принимающим значение 1, может привести к его чрезмерной разнице. Таким образом, нам нужно различать временные ряды, используя дробное значение.

В мире науки о данных нет единой превосходящей модели, модель, которая работает с вашими данными, сильно зависит от вашего набора данных. Знание различных моделей позволяет нам выбирать модель, которая работает с нашими данными и экспериментирует с этой моделью для достижения наилучших результатов. И результаты должны рассматриваться как график, а также метрики ошибок, иногда небольшая ошибка также может быть плохой, следовательно, построение графика и визуализация результатов очень важны.

В следующей главе мы рассмотрим другую статистическую модель — экспоненциальное сглаживание.

Временной ряд — экспоненциальное сглаживание

В этой главе мы поговорим о методах экспоненциального сглаживания временных рядов.

Простое экспоненциальное сглаживание

Экспоненциальное сглаживание — это метод сглаживания одномерных временных рядов путем назначения экспоненциально убывающих весов данным за период времени.

Математически, значение переменной во время ‘t + 1’, заданное значение во время t, y_ (t + 1 | t) определяется как —

yt+1|t= alphayt+ alpha lgroup1− alpha rgroupyt−1+ alpha lgroup1− альфа rgroup2yт−2 +...+у−1

$$y_ {t + 1 | t} \: = \: \ alpha y_ {t} \: + \: \ alpha \ lgroup1 - \ alpha \ rgroup y_ {t-1} \: + \ alpha \ lgroup1- \ альфа \ rgroup ^ {2} \: y_ {т-2} \ + \: ... + у- {1}$$

где 0 leq alpha leq1$0 \ leq \ alpha \ leq1$ — параметр сглаживания, а

y1,....,yt$y_ {1}, ...., y_ {t}$ — предыдущие значения сетевого трафика в моменты времени 1, 2, 3,…, t.

Это простой метод для моделирования временных рядов без четкой тенденции или сезонности. Но экспоненциальное сглаживание также можно использовать для временных рядов с трендом и сезонностью.

Тройное экспоненциальное сглаживание

Тройное экспоненциальное сглаживание (TES) или метод Холта-Винтера применяет трижды экспоненциальное сглаживание — сглаживание уровней lt$l_ {t}$, сглаживание трендов bt$b_ {t}$ и сезонное сглаживание St$S_ {t}$ с помощью  alpha$\ alpha$. ,  beta∗$\ beta ^ {*}$ и  gamma$\ gamma$ как параметры сглаживания, где ‘m’ — частота сезонности, то есть количество сезонов в году.

В соответствии с характером сезонного компонента, TES имеет две категории —

• Аддитивный метод Холта-Винтера — Когда сезонность носит аддитивный характер.

• Мультипликативный метод Холта-Винтера — когда сезонность носит мультипликативный характер.

Аддитивный метод Холта-Винтера — Когда сезонность носит аддитивный характер.

Мультипликативный метод Холта-Винтера — когда сезонность носит мультипликативный характер.

Для несезонных временных рядов у нас есть только сглаживание трендов и сглаживание уровней, которое называется методом линейных трендов Холта.

Давайте попробуем применить тройное экспоненциальное сглаживание к нашим данным.

В [316]:

from statsmodels.tsa.holtwinters import ExponentialSmoothing

model = ExponentialSmoothing(train.values, trend= )
model_fit = model.fit()

В [322]:

predictions_ = model_fit.predict(len(test))

В [325]:

plt.plot(test.values)
plt.plot(predictions_[1:1871])

Из [325]:

[<matplotlib.lines.Line2D at 0x1eab00f1cf8>]

Здесь мы однажды обучили модель с помощью тренировочного набора, а затем продолжаем делать прогнозы. Более реалистичным подходом является переобучение модели после одного или нескольких временных шагов. Поскольку мы получаем прогноз для времени «t + 1» из обучающих данных «до времени» t, следующий прогноз для времени «t + 2» может быть сделан с использованием обучающих данных «до времени» t + 1 »в качестве фактического значение в ‘t + 1’ будет известно тогда. Эта методология составления прогнозов для одного или нескольких будущих шагов, а затем повторного обучения модели называется скользящим прогнозом или валидацией.

Временной ряд — проверка шага вперед

При моделировании временных рядов прогнозы во времени становятся все менее и менее точными, и, следовательно, это более реалистичный подход для переобучения модели фактическими данными, когда она становится доступной для дальнейших прогнозов. Поскольку обучение статистическим моделям не занимает много времени, предварительная проверка является наиболее предпочтительным решением для получения наиболее точных результатов.

Давайте применим проверку наших данных на шаг вперед и сравним ее с результатами, полученными нами ранее.

В [333]:

prediction = []
data = train.values
for t In test.values:
   model = (ExponentialSmoothing(data).fit())
   y = model.predict()
   prediction.append(y[0])
   data = numpy.append(data, t)

В [335]:

test_ = pandas.DataFrame(test)
test_['predictionswf'] = prediction

В [341]:

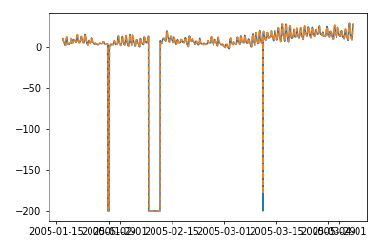
plt.plot(test_['T'])
plt.plot(test_.predictionswf, '--')
plt.show()

В [340]:

error = sqrt(metrics.mean_squared_error(test.values,prediction))
print ('Test RMSE for Triple Exponential Smoothing with Walk-Forward Validation: ', error)
Test RMSE for Triple Exponential Smoothing with Walk-Forward Validation:  11.787532205759442

Мы видим, что наша модель теперь работает значительно лучше. На самом деле, тенденция прослеживается настолько близко, что на графике прогнозы частично совпадают с фактическими значениями. Вы можете попробовать применить предварительную проверку на моделях ARIMA.

Временной ряд — модель пророка

В 2017 году Facebook открыла модель пророка, которая была способна моделировать временные ряды с сильными множественными сезонностями на уровне дня, недели, года и т. Д., А также тенденции. Он имеет интуитивно понятные параметры, которые не очень опытный специалист по данным может настроить для более точных прогнозов. По своей сути это аддитивная регрессивная модель, которая может обнаруживать точки изменения для моделирования временных рядов.

Пророк разбивает временные ряды на составляющие тренда gt$g_ {t}$, сезонности St$S_ {t}$ и праздников ht$h_ {t}$.

у−T=gт+Sт+HT+ epsilonT

$$у- {T} = {g_ т} + S_ {т} + H_ {T} + \ epsilon_ {T}$$

Где  epsilont$\ epsilon_ {t}$ — это термин ошибки.

Подобные пакеты для прогнозирования временных рядов, такие как причинно-следственная связь и обнаружение аномалий, были введены в R Google и Twitter соответственно.

Временной ряд — модель LSTM

Теперь мы знакомы со статистическим моделированием по временным рядам, но машинное обучение сейчас в моде, поэтому важно также знать некоторые модели машинного обучения. Начнем с самой популярной модели в области временных рядов — модели с кратковременной памятью.

LSTM — это класс возвратных нейронных сетей. Поэтому, прежде чем мы сможем перейти к LSTM, важно понять нейронные сети и рекуррентные нейронные сети.

Нейронные сети

Искусственная нейронная сеть представляет собой слоистую структуру из связанных нейронов, вдохновленную биологическими нейронными сетями. Это не один алгоритм, а комбинация различных алгоритмов, которая позволяет нам выполнять сложные операции с данными.

Рекуррентные нейронные сети

Это класс нейронных сетей, предназначенных для работы с временными данными. Нейроны RNN имеют состояние / память ячейки, и ввод обрабатывается в соответствии с этим внутренним состоянием, которое достигается с помощью петель в нейронной сети. В RNN существуют повторяющиеся модули «tanh» слоев, которые позволяют им сохранять информацию. Однако ненадолго, поэтому нам нужны модели LSTM.

LSTM

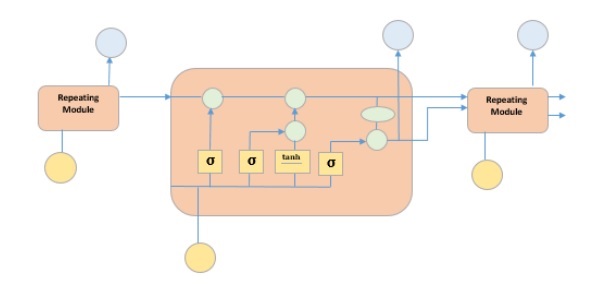
Это особый вид рекуррентной нейронной сети, способной изучать долгосрочные зависимости в данных. Это достигается за счет того, что повторяющийся модуль модели имеет комбинацию четырех слоев, взаимодействующих друг с другом.

На рисунке выше изображены четыре слоя нейронной сети в желтых прямоугольниках, точечные операторы в зеленых кружках, ввод в желтых кружках и состояние ячейки в голубых кружках. Модуль LSTM имеет состояние ячейки и три шлюза, что дает им возможность выборочно изучать, отключать или сохранять информацию от каждого из модулей. Состояние ячейки в LSTM помогает информации проходить через единицы без изменения, позволяя только несколько линейных взаимодействий. Каждое устройство имеет вход, выход и шлюз забывания, который может добавлять или удалять информацию в состояние ячейки. Врата забытия решает, какая информация из предыдущего состояния ячейки должна быть забыта, для чего она использует сигмовидную функцию. Входной вентиль управляет потоком информации в текущем состоянии ячейки, используя точечную операцию умножения sigmoid и tanh соответственно. Наконец, выходной вентиль решает, какую информацию следует передать в следующее скрытое состояние

Теперь, когда мы поняли внутреннюю работу модели LSTM, давайте реализуем ее. Чтобы понять реализацию LSTM, мы начнем с простого примера — прямой линии. Давайте посмотрим, сможет ли LSTM узнать взаимосвязь прямой линии и предсказать ее.

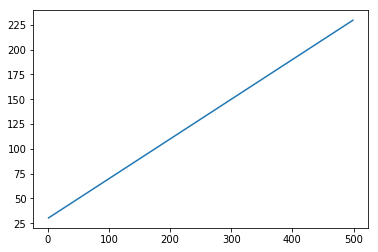
Сначала давайте создадим набор данных, изображающий прямую линию.

В [402]:

x = numpy.arange (1,500,1)
y = 0.4 * x + 30
plt.plot(x,y)

Из [402]:

[<matplotlib.lines.Line2D at 0x1eab9d3ee10>]

В [403]:

trainx, testx = x[0:int(0.8*(len(x)))], x[int(0.8*(len(x))):]
trainy, testy = y[0:int(0.8*(len(y)))], y[int(0.8*(len(y))):]
train = numpy.array(list(zip(trainx,trainy)))
test = numpy.array(list(zip(trainx,trainy)))

Теперь, когда данные были созданы и разбиты на обучающие и тестовые. Давайте преобразуем данные временного ряда в форму контролируемых обучающих данных в соответствии со значением периода оглядки назад, которое, по сути, представляет собой число лагов, которые, как видно, предсказывают значение в момент времени «t».

Так что временной ряд, как это —

time variable_x
t1  x1
t2  x2
 :   :
 :   :
T   xT

Когда период просмотра равен 1, преобразуется в —

x1   x2
x2   x3
 :    :
 :    :
xT-1 xT

В [404]:

def create_dataset(n_X, look_back):
   dataX, dataY = [], []
   for i in range(len(n_X)-look_back):
      a = n_X[i:(i+look_back), ]
      dataX.append(a)
      dataY.append(n_X[i + look_back, ])
   return numpy.array(dataX), numpy.array(dataY)

В [405]:

look_back = 1
trainx,trainy = create_dataset(train, look_back)
testx,testy = create_dataset(test, look_back)

trainx = numpy.reshape(trainx, (trainx.shape[0], 1, 2))
testx = numpy.reshape(testx, (testx.shape[0], 1, 2))

Теперь мы будем тренировать нашу модель.

Небольшие партии обучающих данных показываются в сети, один этап, когда все обучающие данные показываются модели в пакетах и ​​вычисляется ошибка, называется эпохой. Эпохи должны быть запущены до тех пор, пока ошибка не уменьшится.

В [ ]:

from keras.models import Sequential
from keras.layers import LSTM, Dense

model = Sequential()
model.add(LSTM(256, return_sequences = True, input_shape = (trainx.shape[1], 2)))
model.add(LSTM(128,input_shape = (trainx.shape[1], 2)))
model.add(Dense(2))
model.compile(loss = 'mean_squared_error', optimizer = 'adam')
model.fit(trainx, trainy, epochs = 2000, batch_size = 10, verbose = 2, shuffle = False)
model.save_weights('LSTMBasic1.h5')

В [407]:

model.load_weights('LSTMBasic1.h5')
predict = model.predict(testx)

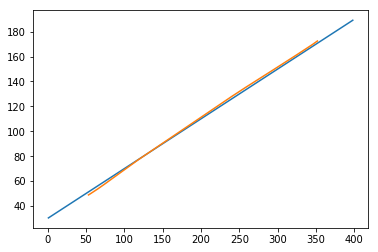
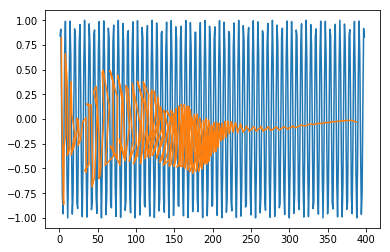
Теперь посмотрим, как выглядят наши прогнозы.

В [408]:

plt.plot(testx.reshape(398,2)[:,0:1], testx.reshape(398,2)[:,1:2])
plt.plot(predict[:,0:1], predict[:,1:2])

Из [408]:

[<matplotlib.lines.Line2D at 0x1eac792f048>]

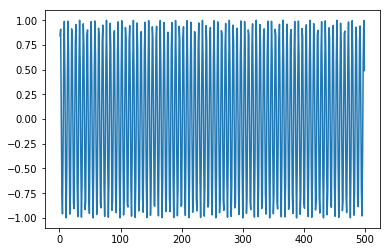
Теперь мы должны попытаться смоделировать волну синуса или косинуса аналогичным образом. Вы можете запустить приведенный ниже код и поиграть с параметрами модели, чтобы увидеть, как меняются результаты.

В [409]:

x = numpy.arange (1,500,1)
y = numpy.sin(x)
plt.plot(x,y)

Из [409]:

[<matplotlib.lines.Line2D at 0x1eac7a0b3c8>]

В [410]:

trainx, testx = x[0:int(0.8*(len(x)))], x[int(0.8*(len(x))):]
trainy, testy = y[0:int(0.8*(len(y)))], y[int(0.8*(len(y))):]
train = numpy.array(list(zip(trainx,trainy)))
test = numpy.array(list(zip(trainx,trainy)))

В [411]:

look_back = 1
trainx,trainy = create_dataset(train, look_back)
testx,testy = create_dataset(test, look_back)
trainx = numpy.reshape(trainx, (trainx.shape[0], 1, 2))
testx = numpy.reshape(testx, (testx.shape[0], 1, 2))

В [ ]:

model = Sequential()
model.add(LSTM(512, return_sequences = True, input_shape = (trainx.shape[1], 2)))
model.add(LSTM(256,input_shape = (trainx.shape[1], 2)))
model.add(Dense(2))
model.compile(loss = 'mean_squared_error', optimizer = 'adam')
model.fit(trainx, trainy, epochs = 2000, batch_size = 10, verbose = 2, shuffle = False)
model.save_weights('LSTMBasic2.h5')

В [413]:

model.load_weights('LSTMBasic2.h5')
predict = model.predict(testx)

В [415]:

plt.plot(trainx.reshape(398,2)[:,0:1], trainx.reshape(398,2)[:,1:2])
plt.plot(predict[:,0:1], predict[:,1:2])

Out [415]:

[<matplotlib.lines.Line2D at 0x1eac7a1f550>]

Теперь вы готовы перейти к любому набору данных.

Временной ряд — Метрики ошибок

Для нас важно количественно оценить производительность модели, чтобы использовать ее в качестве обратной связи и сравнения. В этом уроке мы использовали одну из самых популярных среднеквадратичных ошибок метрики ошибки. Существуют различные другие доступные метрики ошибок. В этой главе они кратко обсуждаются.

Средняя квадратическая ошибка

Это среднее квадрата разницы между прогнозируемыми и истинными значениями. Sklearn предоставляет это как функцию. Он имеет те же единицы, что и квадраты истинных и прогнозируемых значений, и всегда является положительным.

MSE= frac1n displaystyle sum limitnt=1 lgroupy′t−yt rgroup2

$$MSE = \ frac {1} {n} \ displaystyle \ sum \ limit_ {t = 1} ^ n \ lgroup y '_ {t} \: - y_ {t} \ rgroup ^ {2}$$

Где y′t$y '_ {t}$ — прогнозируемое значение,

yt$y_ {t}$ — фактическое значение, и

n — общее количество значений в тестовом наборе.

Из уравнения ясно, что MSE более наказуемо за большие ошибки или выбросы.

Средняя квадратическая ошибка

Это квадратный корень среднеквадратичной ошибки. Это также всегда положительно и находится в диапазоне данных.

RMSE= sqrt frac1n displaystyle sum limitnt=1 lgroupy′t−yt rgroup2

$$RMSE = \ sqrt {\ frac {1} {n} \ displaystyle \ sum \ limit_ {t = 1} ^ n \ lgroup y '_ {t} -y_ {t} \ rgroup ^ 2}$$

Где y′t$y '_ {t}$ — прогнозируемое значение

yt$y_ {t}$ является фактическим значением, и

n — общее количество значений в тестовом наборе.

Он находится во власти единства и, следовательно, более интерпретируем по сравнению с MSE. RMSE также более наказуемо за большие ошибки. Мы использовали RMSE метрику в нашем уроке.

Средняя абсолютная ошибка

Это среднее абсолютной разницы между прогнозируемыми и истинными значениями. Он имеет те же единицы, что и прогнозируемое и истинное значение, и всегда является положительным.

$$ MAE = \ frac {1} {n} \ displaystyle \ sum \ limit_ {t = 1} ^ {t = n} | у ‘{т} -y_ {т} \ lvert $$

Где y′t$y '_ {t}$ — прогнозируемое значение,

yt$y_ {t}$ является фактическим значением, и

n — общее количество значений в тестовом наборе.

Средняя процентная ошибка

Это процент средней абсолютной разницы между прогнозируемыми и истинными значениями, деленный на истинное значение.

MAPE= frac1n displaystyle sum limitnt=1 fracy′t−ytyt∗100%

$$MAPE = \ frac {1} {n} \ displaystyle \ sum \ limit_ {t = 1} ^ n \ frac {y '_ {t} -y_ {t}} {y_ {t}} * 100 \: \%$$

Где y′t$y '_ {t}$ — прогнозируемое значение,

yt$y_ {t}$ — фактическое значение, а n — общее количество значений в тестовом наборе.

Однако недостатком использования этой ошибки является то, что положительная ошибка и отрицательная ошибка могут компенсировать друг друга. Следовательно, используется абсолютная процентная ошибка.

Средняя абсолютная ошибка в процентах

Это процент средней абсолютной разницы между прогнозируемыми и истинными значениями, деленный на истинное значение.

MAPE= frac1n displaystyle sum limitnt=1 frac|y′t−yt lvertyt∗100%

$$MAPE = \ frac {1} {n} \ displaystyle \ sum \ limit_ {t = 1} ^ n \ frac {| y '_ {t} -y_ {t} \ lvert} {y_ {t}} * 100 \: \%$$

Где y′t$y '_ {t}$ — прогнозируемое значение

yt$y_ {t}$ является фактическим значением, и

n — общее количество значений в тестовом наборе.

Временные ряды — Приложения

Мы обсудили анализ временных рядов в этом учебном пособии, который дал нам понимание того, что модели временных рядов сначала распознают тренд и сезонность из существующих наблюдений, а затем прогнозируют значение на основе этой тенденции и сезонности. Такой анализ полезен в различных областях, таких как —

• Финансовый анализ — включает прогнозирование продаж, анализ запасов, анализ фондового рынка, оценку цен.

• Анализ погоды — включает оценку температуры, изменение климата, распознавание сезонных сдвигов, прогноз погоды.

• Анализ сетевых данных — включает прогнозирование использования сети, обнаружение аномалий или вторжений, профилактическое обслуживание.

• Анализ здравоохранения — включает прогнозирование переписи, прогнозирование страховых выплат, мониторинг пациентов.

Финансовый анализ — включает прогнозирование продаж, анализ запасов, анализ фондового рынка, оценку цен.

Анализ погоды — включает оценку температуры, изменение климата, распознавание сезонных сдвигов, прогноз погоды.

Анализ сетевых данных — включает прогнозирование использования сети, обнаружение аномалий или вторжений, профилактическое обслуживание.

Анализ здравоохранения — включает прогнозирование переписи, прогнозирование страховых выплат, мониторинг пациентов.

Временной ряд — дальнейшая сфера

Машинное обучение решает различные проблемы. Фактически, почти все области имеют возможности для автоматизации или улучшения с помощью машинного обучения. Несколько таких проблем, над которыми проводится большая работа, приведены ниже.

Данные временного ряда

Это данные, которые меняются в зависимости от времени, и, следовательно, время играет решающую роль в этом, что мы в основном обсуждали в этом уроке.

Данные не временных рядов

Это данные, не зависящие от времени, и основной процент проблем ОД приходится на данные не временных рядов. Для простоты, мы будем классифицировать его дальше как —

Числовые данные — компьютеры, в отличие от людей, понимают только числа, поэтому в конечном итоге все виды данных преобразуются в числовые данные для машинного обучения, например, данные изображения преобразуются в значения (r, b, g), символы преобразуются в коды ASCII или слова индексируются в числа, речевые данные преобразуются в файлы MFC, содержащие числовые данные.

Данные изображения — компьютерное зрение произвело революцию в мире компьютеров, оно имеет различные применения в области медицины, спутниковой съемки и т. Д.

Текстовые данные — обработка естественного языка (NLP) используется для классификации текста, обнаружения перефразирования и обобщения языка. Это то, что делает Google и Facebook умными.

Данные речи — обработка речи включает в себя распознавание речи и понимание настроения. Он играет решающую роль в придании компьютерам человеческих качеств.