Для стационарного временного ряда модели авторегрессии видят значение переменной в момент времени «t» как линейную функцию от значений «p» временных шагов, предшествующих ему. Математически это можно записать как —
yt=C+ phi1yt−1+ phi2Yt−2+...+ phipyф+ epsilonт
Где ‘p’ — параметр авторегрессивного тренда
epsilont — это белый шум, и
yt−1,yt−2...ytp обозначают значение переменной в предыдущие периоды времени.
Значение p может быть откалибровано с использованием различных методов. Один из способов найти подходящее значение ‘p’ — построить график автокорреляции.
Примечание. Мы должны разделить данные на обучающие и протестировать их в соотношении 8: 2 к общему объему имеющихся данных, прежде чем проводить какой-либо анализ этих данных, поскольку данные тестирования предназначены только для определения точности нашей модели, а допущение о том, что они недоступны для до тех пор, пока не будут сделаны прогнозы. В случае временных рядов последовательность точек данных очень важна, поэтому следует помнить, чтобы не потерять порядок при разделении данных.
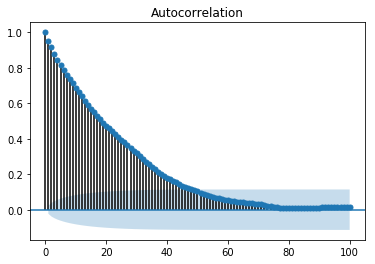
График автокорреляции или коррелограмма показывает отношение переменной к себе на предыдущих временных шагах. Он использует корреляцию Пирсона и показывает корреляции в пределах 95% доверительного интервала. Давайте посмотрим, как это выглядит для переменной температуры наших данных.
Показ ACP
В [141]:
split = len(df) - int(0.2*len(df)) train, test = df['T'][0:split], df['T'][split:]
В [142]:
from statsmodels.graphics.tsaplots import plot_acf plot_acf(train, lags = 100) plt.show()
Предполагается, что все значения запаздывания, лежащие за пределами затененной синей области, имеют корреляцию.