Временной ряд — экспоненциальное сглаживание

В этой главе мы поговорим о методах экспоненциального сглаживания временных рядов.

Простое экспоненциальное сглаживание

Экспоненциальное сглаживание — это метод сглаживания одномерных временных рядов путем назначения экспоненциально убывающих весов данным за период времени.

Математически, значение переменной во время ‘t + 1’, заданное значение во время t, y_ (t + 1 | t) определяется как —

yt+1|t= alphayt+ alpha lgroup1− alpha rgroupyt−1+ alpha lgroup1− альфа rgroup2yт−2 +...+у−1 $$y_ {t + 1 | t} \: = \: \ alpha y_ {t} \: + \: \ alpha \ lgroup1 - \ alpha \ rgroup y_ {t-1} \: + \ alpha \ lgroup1- \ альфа \ rgroup ^ {2} \: y_ {т-2} \ + \: ... + у- {1}$$

где $0 \ leq \ alpha \ leq1$ — параметр сглаживания, а

$y_ {1}, ...., y_ {t}$ — предыдущие значения сетевого трафика в моменты времени 1, 2, 3,…, t.

Это простой метод для моделирования временных рядов без четкой тенденции или сезонности. Но экспоненциальное сглаживание также можно использовать для временных рядов с трендом и сезонностью.

Тройное экспоненциальное сглаживание

Тройное экспоненциальное сглаживание (TES) или метод Холта-Винтера применяет трижды экспоненциальное сглаживание — сглаживание уровней $l_ {t}$, сглаживание трендов $b_ {t}$ и сезонное сглаживание $S_ {t}$ с помощью $\ alpha$. , $\ beta ^ {*}$ и $\ gamma$ как параметры сглаживания, где ‘m’ — частота сезонности, то есть количество сезонов в году.

В соответствии с характером сезонного компонента, TES имеет две категории —

• Аддитивный метод Холта-Винтера — Когда сезонность носит аддитивный характер.

• Мультипликативный метод Холта-Винтера — когда сезонность носит мультипликативный характер.

Аддитивный метод Холта-Винтера — Когда сезонность носит аддитивный характер.

Мультипликативный метод Холта-Винтера — когда сезонность носит мультипликативный характер.

Для несезонных временных рядов у нас есть только сглаживание трендов и сглаживание уровней, которое называется методом линейных трендов Холта.

Давайте попробуем применить тройное экспоненциальное сглаживание к нашим данным.

В [316]:

from statsmodels.tsa.holtwinters import ExponentialSmoothing

model = ExponentialSmoothing(train.values, trend= )
model_fit = model.fit()

В [322]:

predictions_ = model_fit.predict(len(test))

В [325]:

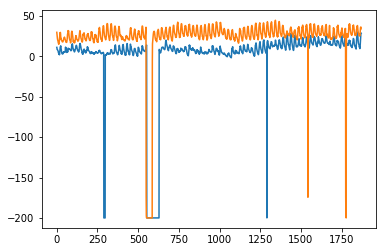
plt.plot(test.values)
plt.plot(predictions_[1:1871])

Из [325]:

[<matplotlib.lines.Line2D at 0x1eab00f1cf8>]

Здесь мы однажды обучили модель с помощью тренировочного набора, а затем продолжаем делать прогнозы. Более реалистичным подходом является переобучение модели после одного или нескольких временных шагов. Поскольку мы получаем прогноз для времени «t + 1» из обучающих данных «до времени» t, следующий прогноз для времени «t + 2» может быть сделан с использованием обучающих данных «до времени» t + 1 »в качестве фактического значение в ‘t + 1’ будет известно тогда. Эта методология составления прогнозов для одного или нескольких будущих шагов, а затем повторного обучения модели называется скользящим прогнозом или валидацией.