Теперь мы знакомы со статистическим моделированием по временным рядам, но машинное обучение сейчас в моде, поэтому важно также знать некоторые модели машинного обучения. Начнем с самой популярной модели в области временных рядов — модели с кратковременной памятью.
LSTM — это класс возвратных нейронных сетей. Поэтому, прежде чем мы сможем перейти к LSTM, важно понять нейронные сети и рекуррентные нейронные сети.
Нейронные сети
Искусственная нейронная сеть представляет собой слоистую структуру из связанных нейронов, вдохновленную биологическими нейронными сетями. Это не один алгоритм, а комбинация различных алгоритмов, которая позволяет нам выполнять сложные операции с данными.
Рекуррентные нейронные сети
Это класс нейронных сетей, предназначенных для работы с временными данными. Нейроны RNN имеют состояние / память ячейки, и ввод обрабатывается в соответствии с этим внутренним состоянием, которое достигается с помощью петель в нейронной сети. В RNN существуют повторяющиеся модули «tanh» слоев, которые позволяют им сохранять информацию. Однако ненадолго, поэтому нам нужны модели LSTM.
LSTM
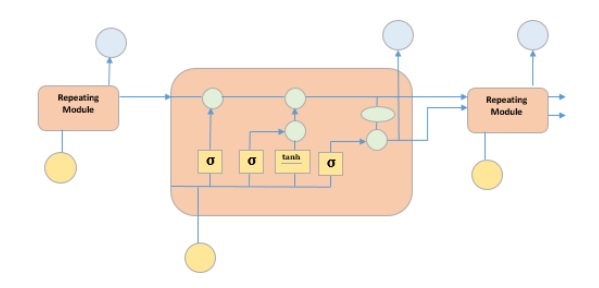
Это особый вид рекуррентной нейронной сети, способной изучать долгосрочные зависимости в данных. Это достигается за счет того, что повторяющийся модуль модели имеет комбинацию четырех слоев, взаимодействующих друг с другом.
На рисунке выше изображены четыре слоя нейронной сети в желтых прямоугольниках, точечные операторы в зеленых кружках, ввод в желтых кружках и состояние ячейки в голубых кружках. Модуль LSTM имеет состояние ячейки и три шлюза, что дает им возможность выборочно изучать, отключать или сохранять информацию от каждого из модулей. Состояние ячейки в LSTM помогает информации проходить через единицы без изменения, позволяя только несколько линейных взаимодействий. Каждое устройство имеет вход, выход и шлюз забывания, который может добавлять или удалять информацию в состояние ячейки. Врата забытия решает, какая информация из предыдущего состояния ячейки должна быть забыта, для чего она использует сигмовидную функцию. Входной вентиль управляет потоком информации в текущем состоянии ячейки, используя точечную операцию умножения sigmoid и tanh соответственно. Наконец, выходной вентиль решает, какую информацию следует передать в следующее скрытое состояние
Теперь, когда мы поняли внутреннюю работу модели LSTM, давайте реализуем ее. Чтобы понять реализацию LSTM, мы начнем с простого примера — прямой линии. Давайте посмотрим, сможет ли LSTM узнать взаимосвязь прямой линии и предсказать ее.
Сначала давайте создадим набор данных, изображающий прямую линию.
В [402]:
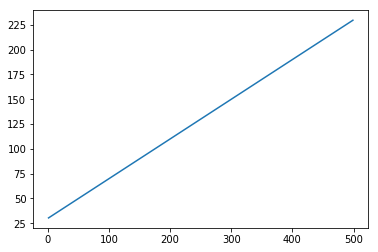
x = numpy.arange (1,500,1) y = 0.4 * x + 30 plt.plot(x,y)
Из [402]:
[<matplotlib.lines.Line2D at 0x1eab9d3ee10>]
В [403]:
trainx, testx = x[0:int(0.8*(len(x)))], x[int(0.8*(len(x))):] trainy, testy = y[0:int(0.8*(len(y)))], y[int(0.8*(len(y))):] train = numpy.array(list(zip(trainx,trainy))) test = numpy.array(list(zip(trainx,trainy)))
Теперь, когда данные были созданы и разбиты на обучающие и тестовые. Давайте преобразуем данные временного ряда в форму контролируемых обучающих данных в соответствии со значением периода оглядки назад, которое, по сути, представляет собой число лагов, которые, как видно, предсказывают значение в момент времени «t».
Так что временной ряд, как это —
time variable_x t1 x1 t2 x2 : : : : T xT
Когда период просмотра равен 1, преобразуется в —
x1 x2 x2 x3 : : : : xT-1 xT
В [404]:
def create_dataset(n_X, look_back):
dataX, dataY = [], []
for i in range(len(n_X)-look_back):
a = n_X[i:(i+look_back), ]
dataX.append(a)
dataY.append(n_X[i + look_back, ])
return numpy.array(dataX), numpy.array(dataY)
В [405]:
look_back = 1 trainx,trainy = create_dataset(train, look_back) testx,testy = create_dataset(test, look_back) trainx = numpy.reshape(trainx, (trainx.shape[0], 1, 2)) testx = numpy.reshape(testx, (testx.shape[0], 1, 2))
Теперь мы будем тренировать нашу модель.
Небольшие партии обучающих данных показываются в сети, один этап, когда все обучающие данные показываются модели в пакетах и вычисляется ошибка, называется эпохой. Эпохи должны быть запущены до тех пор, пока ошибка не уменьшится.
В [ ]:
from keras.models import Sequential
from keras.layers import LSTM, Dense
model = Sequential()
model.add(LSTM(256, return_sequences = True, input_shape = (trainx.shape[1], 2)))
model.add(LSTM(128,input_shape = (trainx.shape[1], 2)))
model.add(Dense(2))
model.compile(loss = 'mean_squared_error', optimizer = 'adam')
model.fit(trainx, trainy, epochs = 2000, batch_size = 10, verbose = 2, shuffle = False)
model.save_weights('LSTMBasic1.h5')
В [407]:
model.load_weights('LSTMBasic1.h5')
predict = model.predict(testx)
Теперь посмотрим, как выглядят наши прогнозы.
В [408]:
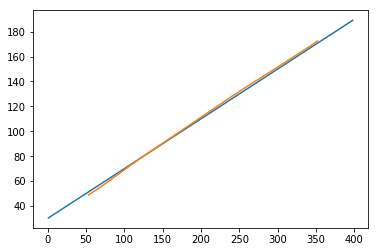
plt.plot(testx.reshape(398,2)[:,0:1], testx.reshape(398,2)[:,1:2]) plt.plot(predict[:,0:1], predict[:,1:2])
Из [408]:
[<matplotlib.lines.Line2D at 0x1eac792f048>]
Теперь мы должны попытаться смоделировать волну синуса или косинуса аналогичным образом. Вы можете запустить приведенный ниже код и поиграть с параметрами модели, чтобы увидеть, как меняются результаты.
В [409]:
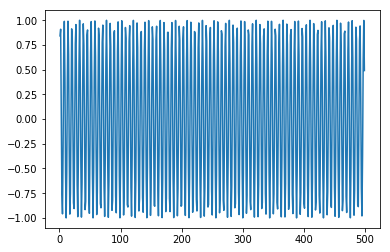
x = numpy.arange (1,500,1) y = numpy.sin(x) plt.plot(x,y)
Из [409]:
[<matplotlib.lines.Line2D at 0x1eac7a0b3c8>]
В [410]:
trainx, testx = x[0:int(0.8*(len(x)))], x[int(0.8*(len(x))):] trainy, testy = y[0:int(0.8*(len(y)))], y[int(0.8*(len(y))):] train = numpy.array(list(zip(trainx,trainy))) test = numpy.array(list(zip(trainx,trainy)))
В [411]:
look_back = 1 trainx,trainy = create_dataset(train, look_back) testx,testy = create_dataset(test, look_back) trainx = numpy.reshape(trainx, (trainx.shape[0], 1, 2)) testx = numpy.reshape(testx, (testx.shape[0], 1, 2))
В [ ]:
model = Sequential()
model.add(LSTM(512, return_sequences = True, input_shape = (trainx.shape[1], 2)))
model.add(LSTM(256,input_shape = (trainx.shape[1], 2)))
model.add(Dense(2))
model.compile(loss = 'mean_squared_error', optimizer = 'adam')
model.fit(trainx, trainy, epochs = 2000, batch_size = 10, verbose = 2, shuffle = False)
model.save_weights('LSTMBasic2.h5')
В [413]:
model.load_weights('LSTMBasic2.h5')
predict = model.predict(testx)
В [415]:
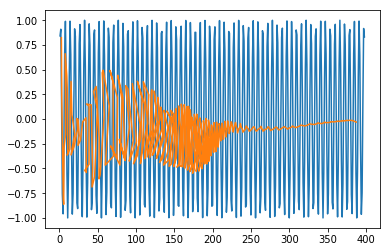
plt.plot(trainx.reshape(398,2)[:,0:1], trainx.reshape(398,2)[:,1:2]) plt.plot(predict[:,0:1], predict[:,1:2])
Out [415]:
[<matplotlib.lines.Line2D at 0x1eac7a1f550>]
Теперь вы готовы перейти к любому набору данных.