Нечеткая логика — теория множеств

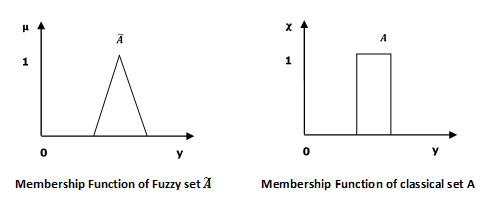
Нечеткие множества можно рассматривать как расширение и грубое упрощение классических множеств. Это может быть лучше понято в контексте членства в наборе. По сути, он допускает частичное членство, что означает, что он содержит элементы с различной степенью членства в наборе. Из этого мы можем понять разницу между классическим множеством и нечетким множеством. Классический набор содержит элементы, которые удовлетворяют точным свойствам членства, в то время как нечеткий набор содержит элементы, которые удовлетворяют неточным свойствам членства.

Математическая концепция

Нечеткое множество $\ widetilde {A}$ во вселенной информации $U$ может быть определено как набор упорядоченных пар, и его можно представить математически как —

$$ \ widetilde {A} = \ left \ {\ left (y, \ mu _ {\ widetilde {A}} \ left (y \ right) \ right) | y \ in U \ right \} $$

Здесь $\ mu _ {\ widetilde {A}} \ left (y \ right)$ = степень принадлежности $y$ в \ widetilde {A}, принимает значения в диапазоне от 0 до 1, т. Е. $\ Mu _ {\ widetilde {A}} (y) \ in \ left [0,1 \ right]$.

Представление нечеткого множества

Давайте теперь рассмотрим два случая вселенной информации и поймем, как можно представить нечеткое множество.

Случай 1

Когда информационная вселенная $U$ дискретна и конечна —

$$\ widetilde {A} = \ left \ {\ frac {\ mu _ {\ widetilde {A}} \ left (y_1 \ right)} {y_1} + \ frac {\ mu _ {\ widetilde {A}} \ left (y_2 \ right)} {y_2} + \ frac {\ mu _ {\ widetilde {A}} \ left (y_3 \ right)} {y_3} + ... \ right \}$$

$= \ left \ {\ sum_ {i = 1} ^ {n} \ frac {\ mu _ {\ widetilde {A}} \ left (y_i \ right)} {y_i} \ right \}$

Дело 2

Когда информационная вселенная $U$ непрерывна и бесконечна —

$$\ widetilde {A} = \ left \ {\ int \ frac {\ mu _ {\ widetilde {A}} \ left (y \ right)} {y} \ right \}$$

В вышеприведенном представлении символ суммирования представляет коллекцию каждого элемента.

Операции над нечеткими множествами

Имея два нечетких множества $\ widetilde {A}$ и $\ widetilde {B}$, универсум информации $U$ и элемент ? вселенной, следующие соотношения выражают операции объединения, пересечения и дополнения на нечетких множествах.

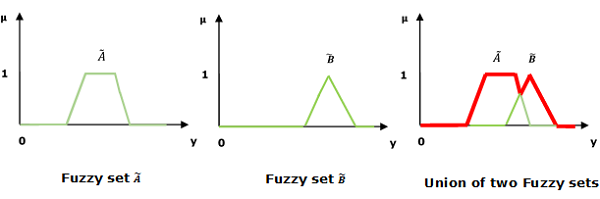
Союз / Нечеткое ‘ИЛИ’

Давайте рассмотрим следующее представление, чтобы понять, как работает отношение Union / Fuzzy ‘OR’ —

$$\ mu _ {{\ widetilde {A} \ cup \ widetilde {B}}} \ left (y \ right) = \ mu _ {\ widetilde {A}} \ vee \ mu _ \ widetilde {B} \ quad \ forall y \ in U$$

Здесь ∨ представляет операцию «max».

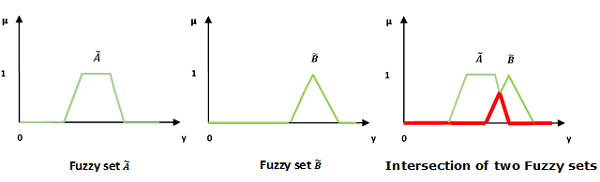
Пересечение / Нечеткое ‘И’

Давайте рассмотрим следующее представление, чтобы понять, как работает отношение Пересечение / Нечеткое ‘И’ —

$$\ mu _ {{\ widetilde {A} \ cap \ widetilde {B}}} \ left (y \ right) = \ mu _ {\ widetilde {A}} \ wedge \ mu _ \ widetilde {B} \ quad \ forall y \ in U$$

Здесь ∧ представляет операцию ‘min’.

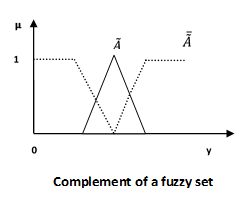
Дополнение / Нечеткое НЕ

Давайте рассмотрим следующее представление, чтобы понять, как работает отношение Complement / Fuzzy ‘NOT’ —

$$\ mu _ {\ widetilde {A}} = 1- \ mu _ {\ widetilde {A}} \ left (y \ right) \ quad y \ in U$$

Свойства нечетких множеств

Давайте обсудим различные свойства нечетких множеств.

Коммутативная собственность

Имея два нечетких множества $\ widetilde {A}$ и $\ widetilde {B}$, это свойство гласит:

$$\ widetilde {A} \ cup \ widetilde {B} = \ widetilde {B} \ cup \ widetilde {A}$$

$$\ widetilde {A} \ cap \ widetilde {B} = \ widetilde {B} \ cap \ widetilde {A}$$

Ассоциативная собственность

Имея три нечетких множества $\ widetilde {A}$, $\ widetilde {B}$ и $\ widetilde {C}$, это свойство гласит:

$$\ widetilde {A} \ cup \ left (\ widetilde {B} \ cup \ widetilde {C} \ right) = \ left (\ widetilde {A} \ cup \ widetilde {B} \ right) \ cup \ widetilde {C},$$

$$\ widetilde {A} \ cap \ left (\ widetilde {B} \ cap \ widetilde {C} \ right) = \ left (\ widetilde {A} \ cup \ widetilde {B} \ right) \ cup \ widetilde {C},$$

Распределительное свойство

Имея три нечетких множества $\ widetilde {A}$, $\ widetilde {B}$ и $\ widetilde {C}$, это свойство гласит:

$$\ widetilde {A} \ cup \ left (\ widetilde {B} \ cap \ widetilde {C} \ right) = \ left (\ widetilde {A} \ cup \ widetilde {B} \ right) \ cap \ left (\ widetilde {A} \ cup \ widetilde {C} \ right)$$

$$\ widetilde {A} \ cap \ left (\ widetilde {B} \ cup \ widetilde {C} \ right) = \ left (\ widetilde {A} \ cap \ widetilde {B} \ right) \ cup \ left (\ widetilde {A} \ cap \ widetilde {C} \ right)$$

Свойство идемпотентности

Для любого нечеткого множества $\ widetilde {A}$ это свойство гласит:

$$\ widetilde {A} \ cup \ widetilde {A} = \ widetilde {A}$$

$$\ widetilde {A} \ cap \ widetilde {A} = \ widetilde {A}$$

Собственность идентичности

Для нечеткого множества $\ widetilde {A}$ и универсального множества $U$ это свойство гласит:

$$\ widetilde {A} \ cup \ varphi = \ widetilde {A}$$

$$\ widetilde {A} \ cap U = \ widetilde {A}$$

$$\ widetilde {A} \ cap \ varphi = \ varphi$$

$$\ widetilde {A} \ cup U = U$$

Переходное свойство

Имея три нечетких множества $\ widetilde {A}$, $\ widetilde {B}$ и $\ widetilde {C}$, это свойство гласит:

If widetildeA subseteq widetildeB subseteq widetildeC,then widetildeA subseteq widetildeC $$If \: \ widetilde {A} \ subseteq \ widetilde {B} \ subseteq \ widetilde {C}, \: then \: \ widetilde {A} \ subseteq \ widetilde {C}$$

Инволюция собственности

Для любого нечеткого множества $\ widetilde {A}$ это свойство гласит:

$$\ overline {\ overline {\ widetilde {A}}} = \ widetilde {A}$$

Закон де Моргана

Этот закон играет решающую роль в доказательстве тавтологии и противоречия. Этот закон гласит:

$$\ overline {{\ widetilde {A} \ cap \ widetilde {B}}} = \ overline {\ widetilde {A}} \ cup \ overline {\ widetilde {B}}$$

$$\ overline {{\ widetilde {A} \ cup \ widetilde {B}}} = \ overline {\ widetilde {A}} \ cap \ overline {\ widetilde {B}}$$