Нечеткая логика — функция членства

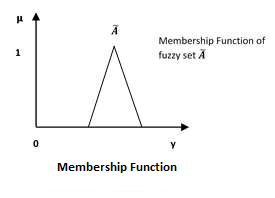
Мы уже знаем, что нечеткая логика — это не нечеткая логика, а логика, которая используется для описания нечеткости. Эта нечеткость лучше всего характеризуется его функцией членства. Другими словами, мы можем сказать, что функция принадлежности представляет степень правды в нечеткой логике.

Ниже приведены несколько важных моментов, касающихся функции членства.

• Функции членства были впервые введены в 1965 году Лофти А. Заде в его первой исследовательской работе «Нечеткие множества».

• Функции принадлежности характеризуют нечеткость (т. Е. Всю информацию в нечетком множестве), независимо от того, являются ли элементы в нечетких множествах дискретными или непрерывными.

• Функции членства можно определить как метод решения практических задач на основе опыта, а не знаний.

• Функции принадлежности представлены графическими формами.

• Правила определения нечеткости тоже нечетки.

Функции членства были впервые введены в 1965 году Лофти А. Заде в его первой исследовательской работе «Нечеткие множества».

Функции принадлежности характеризуют нечеткость (т. Е. Всю информацию в нечетком множестве), независимо от того, являются ли элементы в нечетких множествах дискретными или непрерывными.

Функции членства можно определить как метод решения практических задач на основе опыта, а не знаний.

Функции принадлежности представлены графическими формами.

Правила определения нечеткости тоже нечетки.

Математическая запись

Мы уже изучали, что нечеткое множество М во вселенной информации U может быть определено как множество упорядоченных пар, и оно может быть математически представлено как —

$$ \ widetilde {A} = \ left \ {\ left (y, \ mu _ {\ widetilde {A}} \ left (y \ right) \ right) | y \ in U \ right \} $$

Здесь $\ mu \ widetilde {A} \ left (\ bullet \ right)$ = функция принадлежности $\ widetilde {A}$; это предполагает значения в диапазоне от 0 до 1, т. е. $\ mu \ widetilde {A} \ left (\ bullet \ right) \ in \ left [0,1 \ right]$. Функция принадлежности $\ mu \ widetilde {A} \ left (\ bullet \ right)$ отображает $U$ в пространство принадлежности $M$.

Точка $\ left (\ bullet \ right)$ в функции принадлежности, описанной выше, представляет элемент в нечетком множестве; будь то дискретный или непрерывный.

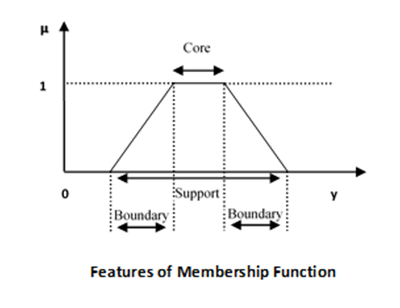
Особенности членских функций

Теперь мы обсудим различные функции функций членства.

ядро

Для любого нечеткого множества $\ widetilde {A}$ ядром функции принадлежности является та область юниверса, которая характеризуется полным членством в наборе. Следовательно, ядро ​​состоит из всех тех элементов $y$ вселенной информации, что

$$\ mu _ {\ widetilde {A}} \ left (y \ right) = 1$$

Служба поддержки

Для любого нечеткого множества $\ widetilde {A}$ поддержка функции принадлежности — это область юниверса, которая характеризуется ненулевым членством в наборе. Следовательно, ядро ​​состоит из всех тех элементов $y$ вселенной информации, что

$$\ mu _ {\ widetilde {A}} \ left (y \ right)> 0$$

граничный

Для любого нечеткого множества $\ widetilde {A}$ границей функции принадлежности является область вселенной, которая характеризуется ненулевым, но неполным членством в множестве. Следовательно, ядро ​​состоит из всех тех элементов $y$ вселенной информации, что

$$1> \ mu _ {\ widetilde {A}} \ left (y \ right)> 0$$

фаззификации

Это может быть определено как процесс преобразования четкого набора в нечеткий набор или нечеткого набора в нечеткий набор. По сути, эта операция переводит точные четкие входные значения в лингвистические переменные.

Ниже приведены два важных метода фаззификации.

Метод Fuzzification (s-fuzzification) поддержки

В этом методе нечеткий набор можно выразить с помощью следующего соотношения:

$$\ widetilde {A} = \ mu _1Q \ left (x_1 \ right) + \ mu _2Q \ left (x_2 \ right) + ... + \ mu _nQ \ left (x_n \ right)$$

Здесь нечеткое множество $Q \ left (x_i \ right)$ называется ядром фаззификации. Этот метод реализован путем сохранения постоянной $\ mu _i$ и преобразования $x_i$ в нечеткое множество $Q \ left (x_i \ right)$.

Метод степенного фаззификации (g-fuzzification)

Он очень похож на описанный выше метод, но основное отличие состоит в том, что он поддерживает постоянную $x_i$, а $\ mu _i$ выражается в виде нечеткого множества.

дефаззификация

Это может быть определено как процесс преобразования нечеткого набора в четкий набор или превращения нечеткого элемента в свежий элемент.

Мы уже изучали, что процесс фаззификации включает преобразование четких величин в нечеткие. В ряде инженерных приложений необходимо дефаззифицировать результат или, скорее, «нечеткий результат», чтобы его можно было преобразовать в четкий результат. Математически процесс дефаззификации также называют «округлением».

Различные методы дефаззификации описаны ниже —

Макс-метод членства

Этот метод ограничен пиковыми выходными функциями и также известен как метод высоты. Математически это можно представить следующим образом:

 mu widetildeA left(x∗ right)> mu widetildeA left(x right)длявсеx inX $$\ mu _ {\ widetilde {A}} \ left (x ^ * \ right)> \ mu _ {\ widetilde {A}} \ left (x \ right) \: для \: все \: x \ in X$$

Здесь $x ^ *$ — дефаззифицированный вывод.

Центроидный метод

Этот метод также известен как центр области или метод центра тяжести. Математически, дефаззифицированный вывод $x ^ *$ будет представлен как —

$$x ^ * = \ frac {\ int \ mu _ {\ widetilde {A}} \ left (x \ right) .xdx} {\ int \ mu _ {\ widetilde {A}} \ left (x \ right) ) .dx}$$

Средневзвешенный метод

В этом методе каждая функция членства взвешивается по максимальному значению членства. Математически, дефаззифицированный вывод $x ^ *$ будет представлен как —

$$x ^ * = \ frac {\ sum \ mu _ {\ widetilde {A}} \ left (\ overline {x_i} \ right). \ overline {x_i}} {\ sum \ mu _ {\ widetilde {A }} \ left (\ overline {x_i} \ right)}$$

Среднее-Макс Членство

Этот метод также известен как середина максимумов. Математически, дефаззифицированный вывод $x ^ *$ будет представлен как —

$$x ^ * = \ frac {\ displaystyle \ sum_ {i = 1} ^ {n} \ overline {x_i}} {n}$$