Нечеткая логика - классическая теория множеств

Набор представляет собой неупорядоченную коллекцию различных элементов. Это может быть написано явно, перечисляя его элементы, используя установленную скобку. Если порядок элементов изменяется или какой-либо элемент набора повторяется, он не вносит никаких изменений в набор.

пример

Набор всех натуральных чисел.
Совокупность всех планет Солнечной системы.
Набор из всех штатов в Индии.
Набор всех строчных букв алфавита.

Математическое представление множества

Наборы могут быть представлены двумя способами —

Реестр или Табличная форма

В этой форме набор представлен перечислением всех элементов, составляющих его. Элементы заключены в фигурные скобки и разделены запятыми.

Ниже приведены примеры набора в Ростере или Табличной Форме —

Набор гласных в английском алфавите, A = {a, e, i, o, u}
Набор нечетных чисел меньше 10, B = {1,3,5,7,9}

Установить нотацию Builder

В этой форме набор определяется путем указания свойства, которое имеют общие элементы набора. Набор описывается как A = {x: p (x)}

Пример 1 — множество {a, e, i, o, u} записывается как

A = {x: x — гласный в английском алфавите}

Пример 2. Набор {1,3,5,7,9} записывается как

B = {x: 1 ≤ x <10 и (x% 2) ≠ 0}

Если элемент x является членом любого множества S, он обозначается x∈S, а если элемент y не является членом множества S, он обозначается y∉S.

Пример — если S = {1,1.2,1.7,2}, 1 ∈ S, но 1,5 ∉ S

Мощность множества

Мощность множества S, обозначаемая | S || S |, — это количество элементов множества. Номер также называется кардинальным числом. Если множество имеет бесконечное число элементов, его мощность равна ∞∞.

Пример — | {1,4,3,5} | = 4, | {1,2,3,4,5,…} | = ∞

Если существует два множества X и Y, | X | = | Y | обозначает два множества X и Y, имеющих одинаковую мощность. Это происходит, когда количество элементов в X точно равно числу элементов в Y. В этом случае существует биективная функция ‘f’ от X до Y.

| X | ≤ | Y | обозначает, что мощность множества X меньше или равна мощности множества Y Это происходит, когда число элементов в X меньше или равно числу элементов в Y. Здесь существует инъективная функция ‘f’ от X до Y.

| X | <| Y | обозначает, что набор элементов X меньше, чем набор элементов Y Это происходит, когда число элементов в X меньше, чем в Y. Здесь функция ‘f’ из X в Y является инъективной функцией, но не биективной.

Если | X | ≤ | Y | и | X | ≤ | Y | тогда | X | = | Y | , Наборы X и Y обычно называют эквивалентными наборами .

Типы Наборов

Наборы могут быть классифицированы на многие типы; некоторые из которых являются конечными, бесконечными, подмножествами, универсальными, собственными, одноэлементными множествами и т.д.

Конечный набор

Множество, которое содержит определенное количество элементов, называется конечным множеством.

Пример — S = {x | x ∈ N и 70> x> 50}

Бесконечный набор

Множество, которое содержит бесконечное количество элементов, называется бесконечным множеством.

Пример — S = {x | x ∈ N и x> 10}

Подмножество

Множество X является подмножеством множества Y (записывается как X ⊆ Y), если каждый элемент X является элементом множества Y.

Пример 1. Пусть X = {1,2,3,4,5,6} и Y = {1,2}. Здесь множество Y является подмножеством множества X, так как все элементы множества Y находятся в множестве X. Следовательно, мы можем написать Y⊆X.

Пример 2. Пусть X = {1,2,3} и Y = {1,2,3}. Здесь множество Y — это подмножество (а не собственное подмножество) множества X, так как все элементы множества Y находятся в множестве X. Следовательно, мы можем записать Y⊆X.

Правильное подмножество

Термин «правильное подмножество» может быть определен как «подмножество, но не равно». Набор X является правильным подмножеством множества Y (записывается как X ⊂ Y), если каждый элемент X является элементом множества Y и | X | <| Y |.

Пример. Пусть X = {1,2,3,4,5,6} и Y = {1,2}. Здесь задайте Y ⊂ X, поскольку все элементы в Y содержатся и в X, и в X есть хотя бы один элемент, превышающий множество Y.

Универсальный комплект

Это коллекция всех элементов в определенном контексте или приложении. Все наборы в этом контексте или приложении по существу являются подмножествами этого универсального набора. Универсальные наборы представлены как U.

Пример. Мы можем определить U как совокупность всех животных на земле. В этом случае набор всех млекопитающих является подмножеством U, набор всех рыб является подмножеством U, набор всех насекомых является подмножеством U и так далее.

Пустой набор или нулевой набор

Пустой набор не содержит элементов. Обозначается через Φ. Поскольку число элементов в пустом множестве конечно, пустое множество является конечным множеством. Мощность пустого набора или нулевого набора равна нулю.

Пример — S = {x | x ∈ N и 7 <x <8} = Φ

Синглтон или блок

Набор Singleton или Unit содержит только один элемент. Одноэлементное множество обозначается {s}.

Пример — S = {x | x ∈ N, 7 <x <9} = {8}

Равный Набор

Если два набора содержат одинаковые элементы, они называются равными.

Пример — если A = {1,2,6} и B = {6,1,2}, они равны, поскольку каждый элемент множества A является элементом множества B, а каждый элемент множества B является элементом множества A ,

Эквивалентный набор

Если мощности двух множеств одинаковы, они называются эквивалентными множествами.

Пример — Если A = {1,2,6} и B = {16,17,22}, они эквивалентны, поскольку мощность A равна количеству элементов B. то есть | A | = | B | = 3

Набор перекрывающихся

Два набора, которые имеют хотя бы один общий элемент, называются перекрывающимися наборами. В случае перекрывающихся наборов —

$n \ left (A \ cup B \ right) = n \ left (A \ right) + n \ left (B \ right) - n \ left (A \ cap B \ right)$

$n \ left (A \ cup B \ right) = n \ left (AB \ right) + n \ left (BA \ right) + n \ left (A \ cap B \ right)$

$n \ left (A \ right) = n \ left (AB \ right) + n \ left (A \ cap B \ right)$

$n \ left (B \ right) = n \ left (BA \ right) + n \ left (A \ cap B \ right)$

Пример — Пусть, A = {1,2,6} и B = {6,12,42}. Существует общий элемент «6», поэтому эти наборы являются перекрывающимися.

Несвязанный набор

Два набора A и B называются непересекающимися, если они не имеют хотя бы одного общего элемента. Следовательно, непересекающиеся множества обладают следующими свойствами:

$n \ left (A \ cap B \ right) = \ phi$

$n \ left (A \ cup B \ right) = n \ left (A \ right) + n \ left (B \ right)$

Пример. Пусть, A = {1,2,6} и B = {7,9,14}, нет ни одного общего элемента, поэтому эти наборы являются перекрывающимися.

Операции над классическими наборами

Операции над множествами включают в себя объединение множеств, пересечение множеств, разность множеств, дополнение множества и декартово произведение.

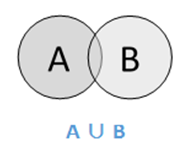
союз

Объединение множеств A и B (обозначаемое A ∪ BA ∪ B) — это множество элементов, которые находятся в A, в B или в A и B. Следовательно, A ∪ B = {x | x ∈ A OR x ∈ B}.

Пример — Если A = {10,11,12,13} и B = {13,14,15}, то A ∪ B = {10,11,12,13,14,15} — Общий элемент встречается только один раз ,

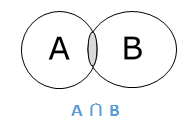
пересечение

Пересечение множеств A и B (обозначаемое A ∩ B) — это множество элементов, которые находятся как в A, так и в B. Следовательно, A ∩ B = {x | x ∈ A и x ∈ B}.

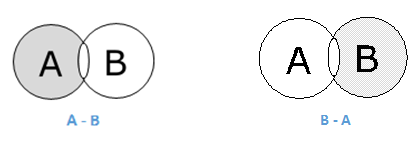
Разница / Относительное дополнение

Разность множеств множеств A и B (обозначаемая A – B) — это множество элементов, которые находятся только в A, но не в B. Следовательно, A — B = {x | x ∈ A и x ∉ B}.

Пример — если A = {10,11,12,13} и B = {13,14,15}, то (A — B) = {10,11,12} и (B — A) = {14,15 }. Здесь мы можем видеть (A — B) ≠ (B — A)

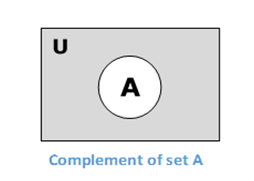
Дополнение набора

Дополнением к множеству A (обозначаемому A ′) является множество элементов, которых нет в множестве A. Следовательно, A ′ = {x | x ∉ A}.

Более конкретно, A ′ = (U-A), где U — универсальное множество, которое содержит все объекты.

Пример — Если A = {x | x принадлежит множеству целых чисел сложения}, то A ′ = {y | y не принадлежит множеству нечетных чисел}

Декартово произведение / кросс произведение

Декартово произведение n числа множеств A1, A2, … An, обозначенное A1 × A2 … × An, может быть определено как все возможные упорядоченные пары (x1, x2,… xn), где x1 ∈ A1, x2 ∈ A2,… xn ∈ An

Пример — если мы возьмем два набора A = {a, b} и B = {1,2},

Декартово произведение A и B записывается как — A × B = {(a, 1), (a, 2), (b, 1), (b, 2)}

И декартово произведение B и A записывается в виде — B × A = {(1, a), (1, b), (2, a), (2, b)}

Свойства классических множеств

Свойства на множествах играют важную роль для получения решения. Ниже приведены различные свойства классических множеств —

Коммутативная собственность

Имея два набора A и B , это свойство гласит:

$A \ cup B = B \ cup A$

$A \ cap B = B \ cap A$

Ассоциативная собственность

Имея три набора A , B и C , это свойство гласит:

$A \ cup \ left (B \ cup C \ right) = \ left (A \ cup B \ right) \ cup C$

$A \ cap \ left (B \ cap C \ right) = \ left (A \ cap B \ right) \ cap C$

Распределительное свойство

Имея три набора A , B и C , это свойство гласит:

$A \ cup \ left (B \ cap C \ right) = \ left (A \ cup B \ right) \ cap \ left (A \ cup C \ right)$

$A \ cap \ left (B \ cup C \ right) = \ left (A \ cap B \ right) \ cup \ left (A \ cap C \ right)$

Свойство идемпотентности

Для любого множества A это свойство гласит:

$A \ cup A = A$

$A \ cap A = A$

Собственность идентичности

Для множества A и универсального множества X это свойство гласит:

$A \ cup \ varphi = A$

$A \ cap X = A$

$A \ cap \ varphi = \ varphi$

$A \ cup X = X$

Переходное свойство

Имея три набора A , B и C , свойство заявляет —

Если $A \ subseteq B \ subseteq C$ , то $A \ subseteq C$

Инволюция собственности