TensorFlow — Рекуррентные нейронные сети

Рекуррентные нейронные сети — это тип глубоко ориентированного на обучение алгоритма, который следует последовательному подходу. В нейронных сетях мы всегда предполагаем, что каждый вход и выход не зависит от всех других слоев. Нейронные сети такого типа называются рекуррентными, потому что они выполняют математические вычисления последовательно.

Рассмотрим следующие шаги для обучения периодической нейронной сети —

Шаг 1 — Введите конкретный пример из набора данных.

Шаг 2 — Сеть возьмет пример и вычислит некоторые вычисления, используя случайно инициализированные переменные.

Шаг 3 — Затем вычисляется прогнозируемый результат.

Шаг 4 — Сравнение фактического результата с ожидаемым значением приведет к ошибке.

Шаг 5 — Чтобы отследить ошибку, она распространяется по тому же пути, где переменные также корректируются.

Шаг 6 — шаги с 1 по 5 повторяются до тех пор, пока мы не убедимся, что переменные, объявленные для получения выходных данных, определены правильно.

Шаг 7 — Систематический прогноз делается путем применения этих переменных, чтобы получить новый невидимый вклад.

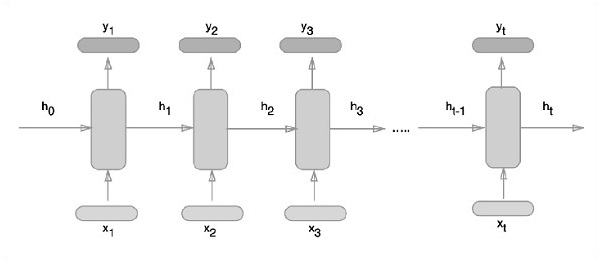
Схематический подход представления рекуррентных нейронных сетей описан ниже —

Рекуррентная реализация нейронной сети с TensorFlow

В этом разделе мы узнаем, как реализовать рекуррентную нейронную сеть с TensorFlow.

Шаг 1 — TensorFlow включает в себя различные библиотеки для конкретной реализации модуля рекуррентной нейронной сети.

#Import necessary modules
from __future__ import print_function

import tensorflow as tf
from tensorflow.contrib import rnn
from tensorflow.examples.tutorials.mnist import input_data
mnist = input_data.read_data_sets("/tmp/data/", one_hot = True)

Как упоминалось выше, библиотеки помогают в определении входных данных, которые составляют основную часть текущей реализации нейронной сети.

Шаг 2 — Наш основной мотив — классифицировать изображения, используя рекуррентную нейронную сеть, где мы рассматриваем каждую строку изображения как последовательность пикселей. Форма изображения MNIST определена как 28 * 28 пикселей. Теперь мы будем обрабатывать 28 последовательностей по 28 шагов для каждого упомянутого образца. Мы определим входные параметры, чтобы получить последовательный шаблон.

n_input = 28 # MNIST data input with img shape 28*28
n_steps = 28
n_hidden = 128
n_classes = 10

# tf Graph input
x = tf.placeholder("float", [None, n_steps, n_input])
y = tf.placeholder("float", [None, n_classes]
weights = {
   'out': tf.Variable(tf.random_normal([n_hidden, n_classes]))
}
biases = {
   'out': tf.Variable(tf.random_normal([n_classes]))
}

Шаг 3 — Вычислите результаты, используя определенную функцию в RNN, чтобы получить наилучшие результаты. Здесь каждая форма данных сравнивается с текущей формой ввода, и результаты вычисляются для поддержания степени точности.

def RNN(x, weights, biases):
   x = tf.unstack(x, n_steps, 1)

   # Define a lstm cell with tensorflow
   lstm_cell = rnn.BasicLSTMCell(n_hidden, forget_bias=1.0)

   # Get lstm cell output
   outputs, states = rnn.static_rnn(lstm_cell, x, dtype = tf.float32)

   # Linear activation, using rnn inner loop last output
   return tf.matmul(outputs[-1], weights['out']) + biases['out']

pred = RNN(x, weights, biases)

# Define loss and optimizer
cost = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(logits = pred, labels = y))
optimizer = tf.train.AdamOptimizer(learning_rate = learning_rate).minimize(cost)

# Evaluate model
correct_pred = tf.equal(tf.argmax(pred,1), tf.argmax(y,1))
accuracy = tf.reduce_mean(tf.cast(correct_pred, tf.float32))

# Initializing the variables
init = tf.global_variables_initializer()

Шаг 4 — На этом шаге мы запустим график, чтобы получить результаты вычислений. Это также помогает при расчете точности результатов испытаний.

with tf.Session() as sess:
   sess.run(init)
   step = 1
   # Keep training until reach max iterations
   
   while step * batch_size < training_iters:
      batch_x, batch_y = mnist.train.next_batch(batch_size)
      batch_x = batch_x.reshape((batch_size, n_steps, n_input))
      sess.run(optimizer, feed_dict={x: batch_x, y: batch_y})
      
      if step % display_step == 0:
         # Calculate batch accuracy
         acc = sess.run(accuracy, feed_dict={x: batch_x, y: batch_y})
         
         # Calculate batch loss
         loss = sess.run(cost, feed_dict={x: batch_x, y: batch_y})
         
         print("Iter " + str(step*batch_size) + ", Minibatch Loss= " + \
            "{:.6f}".format(loss) + ", Training Accuracy= " + \
            "{:.5f}".format(acc))
      step += 1
   print("Optimization Finished!")
      test_len = 128
   test_data = mnist.test.images[:test_len].reshape((-1, n_steps, n_input))
   
   test_label = mnist.test.labels[:test_len]
   print("Testing Accuracy:", \
      sess.run(accuracy, feed_dict={x: test_data, y: test_label}))

На скриншотах ниже показан сгенерированный результат —