TensorFlow — Введение

TensorFlow — это библиотека или структура программного обеспечения, разработанная командой Google для максимально простой реализации концепций машинного обучения и глубокого обучения. Он объединяет вычислительную алгебру методов оптимизации для легкого вычисления многих математических выражений.

Официальный сайт TensorFlow упоминается ниже —

www.tensorflow.org

Давайте теперь рассмотрим следующие важные особенности TensorFlow:

Он включает в себя функцию, которая легко определяет, оптимизирует и вычисляет математические выражения с помощью многомерных массивов, называемых тензорами.
Включает поддержку программирования глубоких нейронных сетей и методов машинного обучения.
Он включает в себя масштабируемую функцию вычислений с различными наборами данных.
TensorFlow использует вычисления на GPU, автоматизируя управление. Он также включает в себя уникальную функцию оптимизации той же памяти и используемых данных.

Он включает в себя функцию, которая легко определяет, оптимизирует и вычисляет математические выражения с помощью многомерных массивов, называемых тензорами.

Включает поддержку программирования глубоких нейронных сетей и методов машинного обучения.

Он включает в себя масштабируемую функцию вычислений с различными наборами данных.

TensorFlow использует вычисления на GPU, автоматизируя управление. Он также включает в себя уникальную функцию оптимизации той же памяти и используемых данных.

Почему TensorFlow так популярен?

TensorFlow хорошо документирован и включает в себя множество библиотек машинного обучения. Он предлагает несколько важных функций и методов для того же.

TensorFlow также называют продуктом «Google». Он включает в себя различные алгоритмы машинного обучения и глубокого обучения. TensorFlow может обучать и запускать глубокие нейронные сети для классификации рукописных цифр, распознавания изображений, встраивания слов и создания различных моделей последовательности.

TensorFlow — Установка

Для установки TensorFlow важно, чтобы в вашей системе был установлен «Python». Python версии 3.4+ считается наилучшим для начала установки TensorFlow.

Для установки TensorFlow в операционной системе Windows выполните следующие шаги.

Шаг 1 — Убедитесь, что версия Python устанавливается.

Шаг 2 — Пользователь может выбрать любой механизм для установки TensorFlow в систему. Мы рекомендуем «Пип» и «Анаконда». Pip — это команда, используемая для выполнения и установки модулей в Python.

Перед установкой TensorFlow нам необходимо установить инфраструктуру Anaconda в нашей системе.

После успешной установки проверьте в командной строке команду «conda». Выполнение команды отображается ниже —

Шаг 3 — Выполните следующую команду, чтобы инициализировать установку TensorFlow —

conda create --name tensorflow python = 3.5

Он загружает необходимые пакеты, необходимые для установки TensorFlow.

Шаг 4 — После успешной настройки среды важно активировать модуль TensorFlow.

activate tensorflow

Шаг 5 — Используйте pip для установки «Tensorflow» в системе. Команда, используемая для установки, упоминается ниже:

pip install tensorflow

А также,

pip install tensorflow-gpu

После успешной установки важно знать пример выполнения программы TensorFlow.

Следующий пример помогает нам понять основную программу создания «Hello World» в TensorFlow.

Код для реализации первой программы упомянут ниже:

>> activate tensorflow
>> python (activating python shell)
>> import tensorflow as tf
>> hello = tf.constant(‘Hello, Tensorflow!’)
>> sess = tf.Session()
>> print(sess.run(hello))

Понимание искусственного интеллекта

Искусственный интеллект включает в себя процесс моделирования человеческого интеллекта с помощью машин и специальных компьютерных систем. Примеры искусственного интеллекта включают обучение, рассуждение и самокоррекцию. Приложения искусственного интеллекта включают распознавание речи, экспертные системы, распознавание изображений и машинное зрение.

Машинное обучение — это отрасль искусственного интеллекта, которая занимается системами и алгоритмами, которые могут изучать любые новые данные и шаблоны данных.

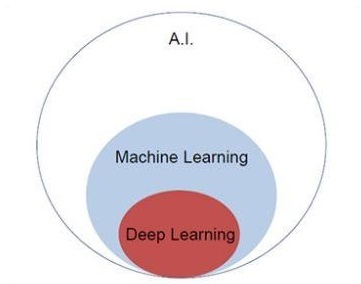
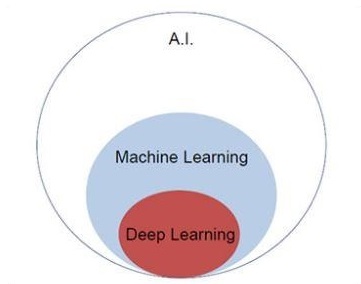
Давайте сосредоточимся на диаграмме Венна, упомянутой ниже, для понимания концепции машинного обучения и глубокого обучения.

Машинное обучение включает в себя раздел машинного обучения, а глубокое обучение является частью машинного обучения. Способность программы, которая следует концепциям машинного обучения, заключается в улучшении характеристик наблюдаемых данных. Основным мотивом преобразования данных является совершенствование своих знаний с целью достижения лучших результатов в будущем, обеспечение вывода, приближенного к желаемому результату для этой конкретной системы. Машинное обучение включает в себя «распознавание образов», которое включает в себя способность распознавать образцы в данных.

Шаблоны должны быть обучены, чтобы показать результат желаемым образом.

Машинное обучение можно обучить двумя разными способами —

Тренировка под наблюдением
Обучение без присмотра

Контролируемое обучение

Контролируемое обучение или контролируемое обучение включает в себя процедуру, в которой обучающий набор дается в качестве входных данных для системы, где каждый пример помечен желаемым выходным значением. Обучение в этом типе выполняется с использованием минимизации конкретной функции потерь, которая представляет ошибку вывода относительно требуемой системы вывода.

После завершения обучения точность каждой модели измеряется в отношении непересекающихся примеров из обучающего набора, также называемого проверочным набором.

Лучший пример для иллюстрации «обучения под наблюдением» — это набор фотографий с информацией, содержащейся в них. Здесь пользователь может обучить модель распознавать новые фотографии.

Обучение без учителя

В обучении без учителя или в обучении без учителя включите примеры обучения, которые не обозначены системой, к которой они относятся. Система ищет данные, которые имеют общие характеристики, и изменяет их, основываясь на внутренних особенностях знаний. Этот тип алгоритмов обучения в основном используется при кластеризации проблем.

Лучший пример для иллюстрации «обучения без учителя» — это набор фотографий без информации и пользовательская модель обучения с классификацией и кластеризацией. Этот тип обучающего алгоритма работает с допущениями, так как информация не предоставляется.

TensorFlow — математические основы

Важно понять математические понятия, необходимые для TensorFlow, прежде чем создавать базовое приложение в TensorFlow. Математика считается сердцем любого алгоритма машинного обучения. Именно с помощью основных понятий математики определяется решение для конкретного алгоритма машинного обучения.

Вектор

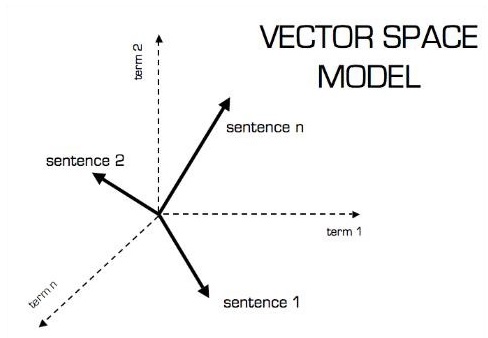
Массив чисел, который является либо непрерывным, либо дискретным, определяется как вектор. Алгоритмы машинного обучения работают с векторами фиксированной длины для лучшего генерирования выходных данных.

Алгоритмы машинного обучения работают с многомерными данными, поэтому векторы играют решающую роль.

Графическое представление векторной модели показано ниже:

скаляр

Скаляр может быть определен как одномерный вектор. Скаляры — это те, которые включают только величину и отсутствие направления. Со скалярами нас интересует только величина.

Примеры скаляров включают в себя параметры веса и роста детей.

матрица

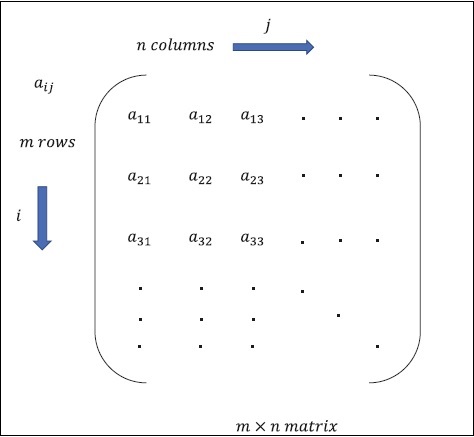
Матрица может быть определена как многомерные массивы, которые расположены в формате строк и столбцов. Размер матрицы определяется длиной строки и длиной столбца. На следующем рисунке показано представление любой указанной матрицы.

Рассмотрим матрицу с «m» строками и «n» столбцами, как упомянуто выше, представление матрицы будет определено как «m * n matrix», которое также определило длину матрицы.

Математические вычисления

В этом разделе мы узнаем о различных математических вычислениях в TensorFlow.

Добавление матриц

Добавление двух или более матриц возможно, если матрицы имеют одинаковое измерение. Добавление подразумевает добавление каждого элемента в соответствии с заданной позицией.

Рассмотрим следующий пример, чтобы понять, как работает сложение матриц:

$$ Пример: A = \ begin {bmatrix} 1 & 2 \\ 3 & 4 \ end {bmatrix} B = \ begin {bmatrix} 5 & 6 \\ 7 & 8 \ end {bmatrix} \: then \: A + B = \ begin {bmatrix} 1 + 5 & 2 + 6 \\ 3 + 7 & 4 + 8 \ end {bmatrix} = \ begin {bmatrix} 6 & 8 \\ 10 & 12 \ end {bmatrix} $$

Вычитание матриц

Вычитание матриц работает аналогично добавлению двух матриц. Пользователь может вычесть две матрицы при условии, что размеры равны.

$$ Пример: A- \ begin {bmatrix} 1 & 2 \\ 3 & 4 \ end {bmatrix} B- \ begin {bmatrix} 5 & 6 \\ 7 & 8 \ end {bmatrix} \: then \: AB — \ begin {bmatrix} 1-5 & 2-6 \\ 3-7 & 4-8 \ end {bmatrix} — \ begin {bmatrix} -4 & -4 \\ — 4 & -4 \ end {bmatrix} $$

Умножение матриц

Для того чтобы две матрицы A m * n и B p * q были умножаемыми, n должно быть равно p . Полученная матрица —

C m * q

$$ A = \ begin {bmatrix} 1 & 2 \\ 3 & 4 \ end {bmatrix} B = \ begin {bmatrix} 5 & 6 \\ 7 & 8 \ end {bmatrix} $$

$$ c_ {11} = \ begin {bmatrix} 1 & 2 \ end {bmatrix} \ begin {bmatrix} 5 \\ 7 \ end {bmatrix} = 1 \ times5 + 2 \ times7 = 19 \: c_ {12} = \ begin {bmatrix} 1 & 2 \ end {bmatrix} \ begin {bmatrix} 6 \\ 8 \ end {bmatrix} = 1 \ times6 + 2 \ times8 = 22 $$

$$ c_ {21} = \ begin {bmatrix} 3 & 4 \ end {bmatrix} \ begin {bmatrix} 5 \\ 7 \ end {bmatrix} = 3 \ times5 + 4 \ times7 = 43 \: c_ {22} = \ begin {bmatrix} 3 & 4 \ end {bmatrix} \ begin {bmatrix} 6 \\ 8 \ end {bmatrix} = 3 \ times6 + 4 \ times8 = 50 $$

$$ C = \ begin {bmatrix} c_ {11} & c_ {12} \\ c_ {21} & c_ {22} \ end {bmatrix} = \ begin {bmatrix} 19 & 22 \\ 43 & 50 \ end {bmatrix} $$

Транспонировать матрицы

Транспонирование матрицы A, m * n обычно представляется AT (транспонирование) n * m и получается путем транспонирования векторов столбцов в качестве векторов строк.

$$ Пример: A = \ begin {bmatrix} 1 & 2 \\ 3 & 4 \ end {bmatrix} \: then \: A ^ {T} \ begin {bmatrix} 1 & 3 \\ 2 & 4 \ end { bmatrix} $$

Точечное произведение векторов

Любой вектор размерности n можно представить в виде матрицы v = R ^ n * 1.

$$ v_ {1} = \ begin {bmatrix} v_ {11} \\ v_ {12} \\\ cdot \\\ cdot \\\ cdot \\ v_ {1n} \ end {bmatrix} v_ {2} = \ begin {bmatrix} v_ {21} \\ v_ {22} \\\ cdot \\\ cdot \\\ cdot \\ v_ {2n} \ end {bmatrix} $$

Точечное произведение двух векторов является суммой произведений соответствующих компонентов — Компонентов вдоль одного измерения и может быть выражено как

$$ v_ {1} \ cdot v_ {2} = v_1 ^ Tv_ {2} = v_2 ^ Tv_ {1} = v_ {11} v_ {21} + v_ {12} v_ {22} + \ cdot \ cdot + v_ {1n} v_ {2n} = \ displaystyle \ sum \ limit_ {k = 1} ^ n v_ {1k} v_ {2k} $$

Пример точечного произведения векторов приведен ниже —

$$ Пример: v_ {1} = \ begin {bmatrix} 1 \\ 2 \\ 3 \ end {bmatrix} v_ {2} = \ begin {bmatrix} 3 \\ 5 \\ — 1 \ end {bmatrix} v_ {1} \ cdot v_ {2} = v_1 ^ Tv_ {2} = 1 \ times3 + 2 \ times5-3 \ times1 = 10 $$

Машинное обучение и глубокое обучение

Искусственный интеллект — одна из самых популярных тенденций последнего времени. Машинное обучение и глубокое обучение составляют искусственный интеллект. Диаграмма Венна, показанная ниже, объясняет взаимосвязь машинного обучения и глубокого обучения —

Машинное обучение

Машинное обучение — это наука о том, как заставить компьютеры действовать в соответствии с алгоритмами, разработанными и запрограммированными. Многие исследователи считают, что машинное обучение — лучший способ достичь ИИ на уровне человека. Машинное обучение включает в себя следующие типы моделей

Контролируемая модель обучения
Необучаемая модель обучения

Глубокое обучение

Глубокое обучение — это подполе машинного обучения, где соответствующие алгоритмы вдохновлены структурой и функциями мозга, называемыми искусственными нейронными сетями.

Вся ценность глубокого обучения сегодня заключается в контролируемом обучении или обучении с использованием маркированных данных и алгоритмов.

Каждый алгоритм глубокого обучения проходит один и тот же процесс. Он включает в себя иерархию нелинейного преобразования входных данных, которые можно использовать для создания статистической модели в качестве выходных данных.

Рассмотрим следующие шаги, которые определяют процесс машинного обучения

Идентифицирует соответствующие наборы данных и подготавливает их для анализа.
Выбирает тип алгоритма для использования
Создает аналитическую модель на основе используемого алгоритма.
Обучает модель на тестовых наборах данных, пересматривая ее по мере необходимости.
Запускает модель для генерации результатов тестов.

Разница между машинным обучением и глубоким обучением

В этом разделе мы узнаем о разнице между машинным обучением и глубоким обучением.

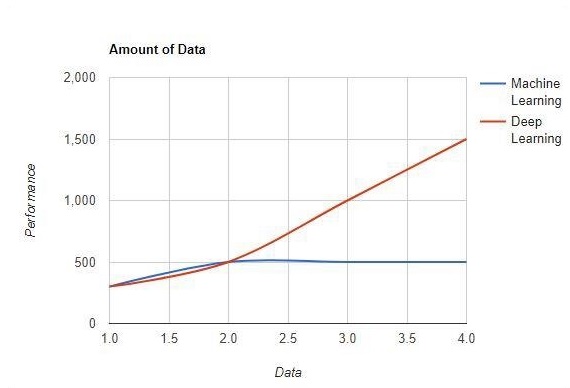
Количество данных

Машинное обучение работает с большими объемами данных. Это полезно для небольших объемов данных тоже. Глубокое обучение, с другой стороны, работает эффективно, если объем данных быстро увеличивается. Следующая диаграмма показывает работу машинного обучения и глубокого обучения с количеством данных —

Аппаратные зависимости

Алгоритмы глубокого обучения предназначены для сильной зависимости от высокопроизводительных машин в отличие от традиционных алгоритмов машинного обучения. Алгоритмы глубокого обучения выполняют ряд операций умножения матриц, которые требуют большого количества аппаратной поддержки.

Характеристика

Проектирование функций — это процесс внедрения знаний в предметные области в определенные функции, чтобы уменьшить сложность данных и создать шаблоны, которые будут видны алгоритмам обучения, с которыми он работает.

Пример. Традиционные шаблоны машинного обучения фокусируются на пикселях и других атрибутах, необходимых для процесса разработки функций. Алгоритмы глубокого обучения ориентированы на высокоуровневые возможности данных. Это уменьшает задачу разработки экстрактора новых функций для каждой новой проблемы.

Подход к решению проблем

Традиционные алгоритмы машинного обучения следуют стандартной процедуре для решения проблемы. Он разбивает проблему на части, решает каждую из них и объединяет их, чтобы получить требуемый результат. Глубокое обучение фокусируется на решении проблемы от конца до конца, а не разбивает их на подразделения.

Время исполнения

Время выполнения — это количество времени, необходимое для обучения алгоритма. Глубокое обучение требует много времени для обучения, так как оно включает много параметров, которые занимают больше времени, чем обычно. Алгоритм машинного обучения сравнительно требует меньше времени выполнения.

Интерпретируемость

Интерпретируемость является основным фактором для сравнения алгоритмов машинного обучения и глубокого обучения. Основная причина заключается в том, что глубокому обучению еще предстоит подумать, прежде чем использовать его в промышленности.

Применение машинного обучения и глубокого обучения

В этом разделе мы узнаем о различных применениях машинного обучения и глубокого обучения.

Компьютерное зрение, которое используется для распознавания лиц и следов посещаемости через отпечатки пальцев или идентификацию транспортного средства через номерной знак.
Поиск информации из поисковых систем, таких как текстовый поиск для поиска изображений.
Автоматизированный почтовый маркетинг с указанием целевой идентификации.
Медицинский диагноз раковых опухолей или выявление аномалий любого хронического заболевания.
Обработка естественного языка для таких приложений, как фото-теги. Лучший пример для объяснения этого сценария используется в Facebook.
Он-лайн реклама.

Компьютерное зрение, которое используется для распознавания лиц и следов посещаемости через отпечатки пальцев или идентификацию транспортного средства через номерной знак.

Поиск информации из поисковых систем, таких как текстовый поиск для поиска изображений.

Автоматизированный почтовый маркетинг с указанием целевой идентификации.

Медицинский диагноз раковых опухолей или выявление аномалий любого хронического заболевания.

Обработка естественного языка для таких приложений, как фото-теги. Лучший пример для объяснения этого сценария используется в Facebook.

Он-лайн реклама.

Будущие тенденции

В связи с растущей тенденцией использования данных и машинного обучения в отрасли для каждой организации будет важно внедрять машинное обучение в своих предприятиях.
Глубокое обучение приобретает все большее значение, чем машинное обучение. Глубокое обучение оказывается одним из лучших методов в современном исполнении.
Машинное обучение и глубокое обучение окажутся полезными в исследовательской и академической сфере.

В связи с растущей тенденцией использования данных и машинного обучения в отрасли для каждой организации будет важно внедрять машинное обучение в своих предприятиях.

Глубокое обучение приобретает все большее значение, чем машинное обучение. Глубокое обучение оказывается одним из лучших методов в современном исполнении.

Машинное обучение и глубокое обучение окажутся полезными в исследовательской и академической сфере.

Заключение

В этой статье у нас был обзор машинного обучения и глубокого обучения с иллюстрациями и различиями, также с акцентом на будущие тенденции. Многие приложения AI используют алгоритмы машинного обучения, прежде всего, для обеспечения самообслуживания, повышения производительности агентов и повышения надежности рабочих процессов. Алгоритмы машинного обучения и глубокого обучения включают захватывающую перспективу для многих предприятий и лидеров отрасли.

TensorFlow — Основы

В этой главе мы узнаем об основах TensorFlow. Начнем с понимания структуры данных тензора.

Тензорная структура данных

Тензорные элементы используются в качестве основных структур данных в языке TensorFlow. Тензорные элементы представляют соединительные ребра в любой блок-схеме, называемой графиком потока данных. Тензоры определяются как многомерный массив или список.

Тензоры идентифицируются по следующим трем параметрам:

Ранг

Единица размерности, описанная в тензоре, называется рангом. Он идентифицирует количество измерений тензора. Ранг тензора можно описать как порядок или n-размерность тензора.

форма

Количество строк и столбцов вместе определяют форму Tensor.

Тип

Тип описывает тип данных, назначенный элементам Tensor.

Пользователь должен рассмотреть следующие действия для построения Tensor —

Построить n-мерный массив
Преобразовать n-мерный массив.

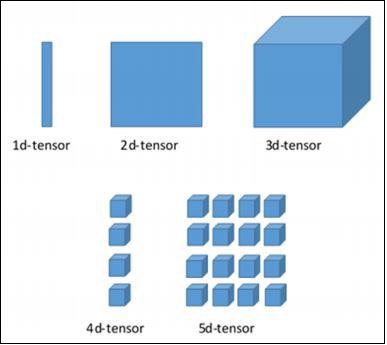
Различные размеры TensorFlow

TensorFlow включает в себя различные размеры. Размеры описаны вкратце ниже —

Одномерный тензор

Одномерный тензор — это нормальная структура массива, которая включает в себя один набор значений одного и того же типа данных.

декларация

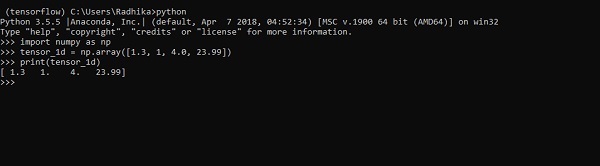
>>> import numpy as np
>>> tensor_1d = np.array([1.3, 1, 4.0, 23.99])
>>> print tensor_1d

Реализация с выводом показана на скриншоте ниже —

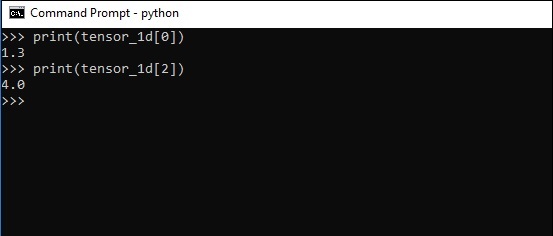
Индексирование элементов такое же, как списки Python. Первый элемент начинается с индекса 0; чтобы распечатать значения через индекс, все, что вам нужно сделать, это указать номер индекса.

>>> print tensor_1d[0]
1.3
>>> print tensor_1d[2]
4.0

Двумерные тензоры

Последовательность массивов используется для создания «двумерных тензоров».

Создание двумерных тензоров описано ниже —

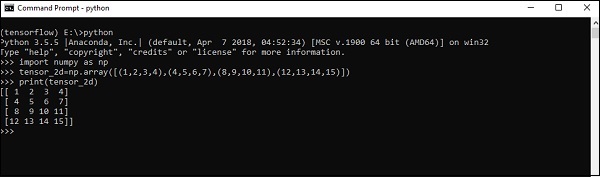
Ниже приводится полный синтаксис для создания двумерных массивов:

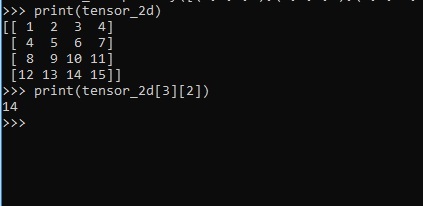
>>> import numpy as np
>>> tensor_2d = np.array([(1,2,3,4),(4,5,6,7),(8,9,10,11),(12,13,14,15)])
>>> print(tensor_2d)
[[ 1 2 3 4]
[ 4 5 6 7]
[ 8 9 10 11]
[12 13 14 15]]
>>>

Конкретные элементы двумерных тензоров можно отслеживать с помощью номера строки и номера столбца, указанных в качестве порядковых номеров.

>>> tensor_2d[3][2]
14

Тензорная обработка и манипуляции

В этом разделе мы узнаем о Tensor Handling и Manipulations.

Для начала рассмотрим следующий код —

import tensorflow as tf
import numpy as np

matrix1 = np.array([(2,2,2),(2,2,2),(2,2,2)],dtype = 'int32')
matrix2 = np.array([(1,1,1),(1,1,1),(1,1,1)],dtype = 'int32')

print (matrix1)
print (matrix2)

matrix1 = tf.constant(matrix1)
matrix2 = tf.constant(matrix2)
matrix_product = tf.matmul(matrix1, matrix2)
matrix_sum = tf.add(matrix1,matrix2)
matrix_3 = np.array([(2,7,2),(1,4,2),(9,0,2)],dtype = 'float32')
print (matrix_3)

matrix_det = tf.matrix_determinant(matrix_3)
with tf.Session() as sess:
   result1 = sess.run(matrix_product)
   result2 = sess.run(matrix_sum)
   result3 = sess.run(matrix_det)

print (result1)
print (result2)
print (result3)

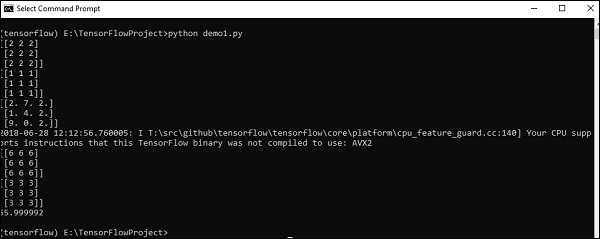
Выход

Приведенный выше код сгенерирует следующий вывод:

объяснение

Мы создали многомерные массивы в приведенном выше исходном коде. Теперь важно понимать, что мы создали график и сеансы, которые управляют тензорами и генерируют соответствующий вывод. С помощью графика у нас есть выходные данные, определяющие математические вычисления между тензорами.

TensorFlow — сверточные нейронные сети

После понимания концепций машинного обучения мы можем переключить наше внимание на концепции глубокого обучения. Глубокое обучение является разделом машинного обучения и считается решающим шагом, предпринятым исследователями в последние десятилетия. Примеры реализации глубокого обучения включают в себя такие приложения, как распознавание изображений и распознавание речи.

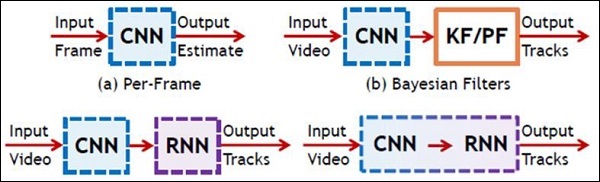
Ниже приведены два важных типа глубоких нейронных сетей —

Сверточные нейронные сети
Рекуррентные нейронные сети

В этой главе мы сосредоточимся на CNN, сверточных нейронных сетях.

Сверточные нейронные сети

Сверточные нейронные сети предназначены для обработки данных через несколько уровней массивов. Этот тип нейронных сетей используется в таких приложениях, как распознавание изображений или распознавание лиц. Основное различие между CNN и любой другой обычной нейронной сетью состоит в том, что CNN принимает входные данные в виде двумерного массива и работает непосредственно с изображениями, а не фокусируется на извлечении признаков, на котором сосредоточены другие нейронные сети.

Доминирующий подход CNN включает в себя решения проблем распознавания. Ведущие компании, такие как Google и Facebook, вложили средства в исследования и разработки для реализации проектов по распознаванию, чтобы ускорить процесс.

Сверточная нейронная сеть использует три основных идеи —

Местные соответствующие поля
свертка
объединение

Позвольте нам понять эти идеи в деталях.

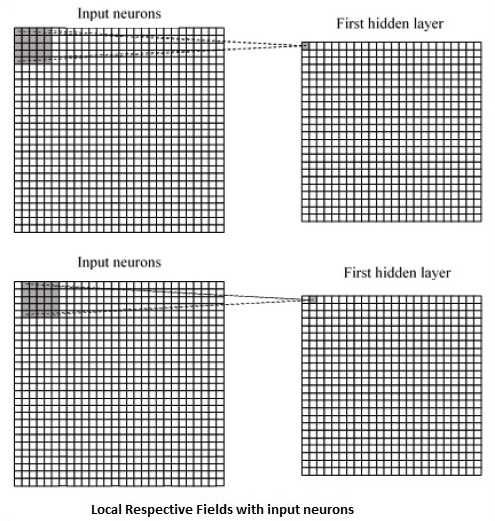
CNN использует пространственные корреляции, которые существуют во входных данных. Каждый параллельный слой нейронной сети соединяет несколько входных нейронов. Этот конкретный регион называется локальным рецептивным полем. Местное рецептивное поле фокусируется на скрытых нейронах. Скрытые нейроны обрабатывают входные данные внутри упомянутого поля, не осознавая изменений за пределами определенной границы.

Ниже приведено схематическое представление генерации соответствующих полей:

Если мы наблюдаем вышеупомянутое представление, каждое соединение узнает вес скрытого нейрона с ассоциированной связью с перемещением от одного слоя к другому. Здесь отдельные нейроны время от времени выполняют сдвиг. Этот процесс называется «свертка».

Отображение соединений от входного слоя к карте скрытых объектов определяется как «общие веса», а включенное смещение называется «общим смещением».

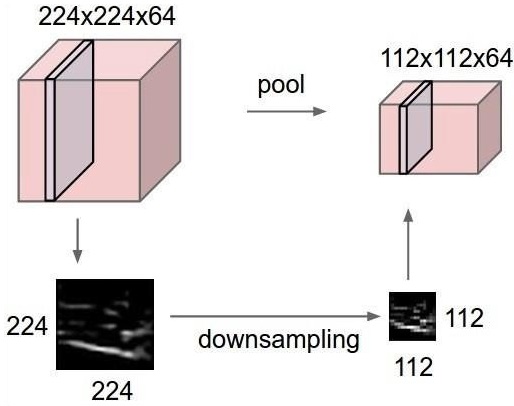
CNN или сверточные нейронные сети используют уровни объединения, которые являются уровнями, расположенными сразу после объявления CNN. Он принимает входные данные пользователя в виде карты объектов, которая выходит из сверточных сетей и подготавливает сжатую карту объектов. Объединение слоев помогает в создании слоев с нейронами предыдущих слоев.

Внедрение TensorFlow CNN

В этом разделе мы узнаем о реализации CNN TensorFlow. Шаги, которые требуют выполнения и правильного измерения всей сети, как показано ниже —

Шаг 1 — Включите необходимые модули для TensorFlow и модули набора данных, которые необходимы для вычисления модели CNN.

import tensorflow as tf
import numpy as np
from tensorflow.examples.tutorials.mnist import input_data

Шаг 2 — Объявите функцию run_cnn () , которая включает в себя различные параметры и переменные оптимизации с объявлением заполнителей данных. Эти переменные оптимизации объявят схему обучения.

def run_cnn():
   mnist = input_data.read_data_sets("MNIST_data/", one_hot = True)
   learning_rate = 0.0001
   epochs = 10
   batch_size = 50

Шаг 3 — На этом шаге мы объявим заполнители обучающих данных с входными параметрами — для 28 x 28 пикселей = 784. Это сглаженные данные изображения, которые извлекаются из mnist.train.nextbatch () .

Мы можем изменить форму тензора в соответствии с нашими требованиями. Первое значение (-1) указывает функции динамически формировать это измерение на основе объема данных, переданных ему. Два средних размера установлены на размер изображения (то есть 28 х 28).

x = tf.placeholder(tf.float32, [None, 784])
x_shaped = tf.reshape(x, [-1, 28, 28, 1])
y = tf.placeholder(tf.float32, [None, 10])

Шаг 4 — Теперь важно создать несколько сверточных слоев —

layer1 = create_new_conv_layer(x_shaped, 1, 32, [5, 5], [2, 2], name = 'layer1')
layer2 = create_new_conv_layer(layer1, 32, 64, [5, 5], [2, 2], name = 'layer2')

Шаг 5 — Давайте сгладим выход, готовый для полностью подключенного выходного каскада — после объединения двух слоев шага 2 с размерами 28 x 28, до размера 14 x 14 или минимум 7 x 7 x, y координаты, но с 64 выходными каналами. Чтобы создать полностью связанный с «плотным» слоем, новая форма должна быть [-1, 7 х 7 х 64]. Мы можем установить некоторые веса и значения смещения для этого слоя, а затем активировать с помощью ReLU.

flattened = tf.reshape(layer2, [-1, 7 * 7 * 64])

wd1 = tf.Variable(tf.truncated_normal([7 * 7 * 64, 1000], stddev = 0.03), name = 'wd1')
bd1 = tf.Variable(tf.truncated_normal([1000], stddev = 0.01), name = 'bd1')

dense_layer1 = tf.matmul(flattened, wd1) + bd1
dense_layer1 = tf.nn.relu(dense_layer1)

Шаг 6 — Другой уровень с определенными активациями softmax с требуемым оптимизатором определяет оценку точности, которая выполняет настройку оператора инициализации.

wd2 = tf.Variable(tf.truncated_normal([1000, 10], stddev = 0.03), name = 'wd2')
bd2 = tf.Variable(tf.truncated_normal([10], stddev = 0.01), name = 'bd2')

dense_layer2 = tf.matmul(dense_layer1, wd2) + bd2
y_ = tf.nn.softmax(dense_layer2)

cross_entropy = tf.reduce_mean(
   tf.nn.softmax_cross_entropy_with_logits(logits = dense_layer2, labels = y))

optimiser = tf.train.AdamOptimizer(learning_rate = learning_rate).minimize(cross_entropy)

correct_prediction = tf.equal(tf.argmax(y, 1), tf.argmax(y_, 1))
accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))

init_op = tf.global_variables_initializer()

Шаг 7 — Мы должны установить переменные записи. Это добавляет сводку для хранения точности данных.

tf.summary.scalar('accuracy', accuracy)
   merged = tf.summary.merge_all()
   writer = tf.summary.FileWriter('E:\TensorFlowProject')
   
   with tf.Session() as sess:
      sess.run(init_op)
      total_batch = int(len(mnist.train.labels) / batch_size)
      
      for epoch in range(epochs):
         avg_cost = 0
      for i in range(total_batch):
         batch_x, batch_y = mnist.train.next_batch(batch_size = batch_size)
            _, c = sess.run([optimiser, cross_entropy], feed_dict = {
            x:batch_x, y: batch_y})
            avg_cost += c / total_batch
         test_acc = sess.run(accuracy, feed_dict = {x: mnist.test.images, y:
            mnist.test.labels})
            summary = sess.run(merged, feed_dict = {x: mnist.test.images, y:
            mnist.test.labels})
         writer.add_summary(summary, epoch)

   print("\nTraining complete!")
   writer.add_graph(sess.graph)
   print(sess.run(accuracy, feed_dict = {x: mnist.test.images, y:
      mnist.test.labels}))

def create_new_conv_layer(
   input_data, num_input_channels, num_filters,filter_shape, pool_shape, name):

   conv_filt_shape = [
      filter_shape[0], filter_shape[1], num_input_channels, num_filters]

   weights = tf.Variable(
      tf.truncated_normal(conv_filt_shape, stddev = 0.03), name = name+'_W')
   bias = tf.Variable(tf.truncated_normal([num_filters]), name = name+'_b')

#Out layer defines the output
   out_layer =
      tf.nn.conv2d(input_data, weights, [1, 1, 1, 1], padding = 'SAME')

   out_layer += bias
   out_layer = tf.nn.relu(out_layer)
   ksize = [1, pool_shape[0], pool_shape[1], 1]
   strides = [1, 2, 2, 1]
   out_layer = tf.nn.max_pool(
      out_layer, ksize = ksize, strides = strides, padding = 'SAME')

   return out_layer

if __name__ == "__main__":
run_cnn()

Ниже приведен вывод, сгенерированный вышеуказанным кодом —

See @{tf.nn.softmax_cross_entropy_with_logits_v2}.

2018-09-19 17:22:58.802268: I
T:\src\github\tensorflow\tensorflow\core\platform\cpu_feature_guard.cc:140]
Your CPU supports instructions that this TensorFlow binary was not compiled to
use: AVX2

2018-09-19 17:25:41.522845: W
T:\src\github\tensorflow\tensorflow\core\framework\allocator.cc:101] Allocation
of 1003520000 exceeds 10% of system memory.

2018-09-19 17:25:44.630941: W
T:\src\github\tensorflow\tensorflow\core\framework\allocator.cc:101] Allocation
of 501760000 exceeds 10% of system memory.

Epoch: 1 cost = 0.676 test accuracy: 0.940

2018-09-19 17:26:51.987554: W
T:\src\github\tensorflow\tensorflow\core\framework\allocator.cc:101] Allocation
of 1003520000 exceeds 10% of system memory.

TensorFlow — Рекуррентные нейронные сети

Рекуррентные нейронные сети — это тип глубоко ориентированного на обучение алгоритма, который следует последовательному подходу. В нейронных сетях мы всегда предполагаем, что каждый вход и выход не зависит от всех других слоев. Нейронные сети такого типа называются рекуррентными, потому что они выполняют математические вычисления последовательно.

Рассмотрим следующие шаги для обучения периодической нейронной сети —

Шаг 1 — Введите конкретный пример из набора данных.

Шаг 2 — Сеть возьмет пример и вычислит некоторые вычисления, используя случайно инициализированные переменные.

Шаг 3 — Затем вычисляется прогнозируемый результат.

Шаг 4 — Сравнение фактического результата с ожидаемым значением приведет к ошибке.

Шаг 5 — Чтобы отследить ошибку, она распространяется по тому же пути, где переменные также корректируются.

Шаг 6 — шаги с 1 по 5 повторяются до тех пор, пока мы не убедимся, что переменные, объявленные для получения выходных данных, определены правильно.

Шаг 7 — Систематический прогноз делается путем применения этих переменных, чтобы получить новый невидимый вклад.

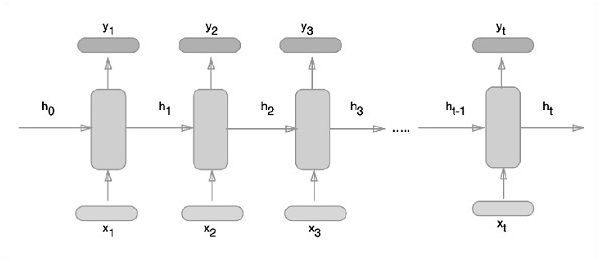
Схематический подход представления рекуррентных нейронных сетей описан ниже —

Рекуррентная реализация нейронной сети с TensorFlow

В этом разделе мы узнаем, как реализовать рекуррентную нейронную сеть с TensorFlow.

Шаг 1 — TensorFlow включает в себя различные библиотеки для конкретной реализации модуля рекуррентной нейронной сети.

#Import necessary modules
from __future__ import print_function

import tensorflow as tf
from tensorflow.contrib import rnn
from tensorflow.examples.tutorials.mnist import input_data
mnist = input_data.read_data_sets("/tmp/data/", one_hot = True)

Как упоминалось выше, библиотеки помогают в определении входных данных, которые составляют основную часть текущей реализации нейронной сети.

Шаг 2 — Наш основной мотив — классифицировать изображения, используя рекуррентную нейронную сеть, где мы рассматриваем каждую строку изображения как последовательность пикселей. Форма изображения MNIST определена как 28 * 28 пикселей. Теперь мы будем обрабатывать 28 последовательностей по 28 шагов для каждого упомянутого образца. Мы определим входные параметры, чтобы получить последовательный шаблон.

n_input = 28 # MNIST data input with img shape 28*28
n_steps = 28
n_hidden = 128
n_classes = 10

# tf Graph input
x = tf.placeholder("float", [None, n_steps, n_input])
y = tf.placeholder("float", [None, n_classes]
weights = {
   'out': tf.Variable(tf.random_normal([n_hidden, n_classes]))
}
biases = {
   'out': tf.Variable(tf.random_normal([n_classes]))
}

Шаг 3 — Вычислите результаты, используя определенную функцию в RNN, чтобы получить наилучшие результаты. Здесь каждая форма данных сравнивается с текущей формой ввода, и результаты вычисляются для поддержания степени точности.

def RNN(x, weights, biases):
   x = tf.unstack(x, n_steps, 1)

   # Define a lstm cell with tensorflow
   lstm_cell = rnn.BasicLSTMCell(n_hidden, forget_bias=1.0)

   # Get lstm cell output
   outputs, states = rnn.static_rnn(lstm_cell, x, dtype = tf.float32)

   # Linear activation, using rnn inner loop last output
   return tf.matmul(outputs[-1], weights['out']) + biases['out']

pred = RNN(x, weights, biases)

# Define loss and optimizer
cost = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(logits = pred, labels = y))
optimizer = tf.train.AdamOptimizer(learning_rate = learning_rate).minimize(cost)

# Evaluate model
correct_pred = tf.equal(tf.argmax(pred,1), tf.argmax(y,1))
accuracy = tf.reduce_mean(tf.cast(correct_pred, tf.float32))

# Initializing the variables
init = tf.global_variables_initializer()

Шаг 4 — На этом шаге мы запустим график, чтобы получить результаты вычислений. Это также помогает при расчете точности результатов испытаний.

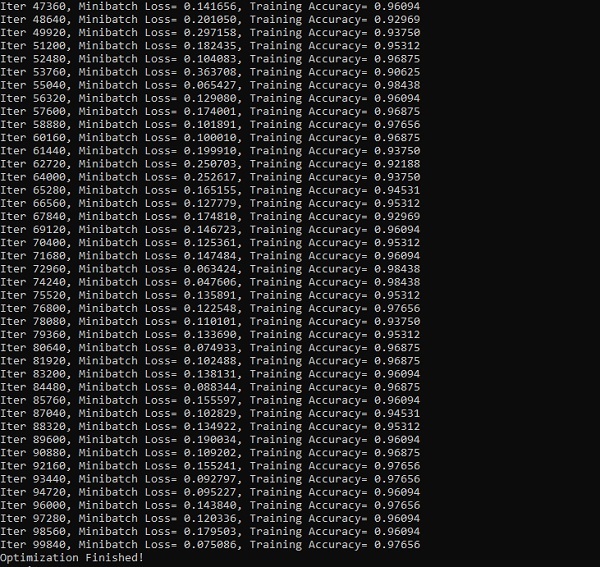
with tf.Session() as sess:
   sess.run(init)
   step = 1
   # Keep training until reach max iterations
   
   while step * batch_size < training_iters:
      batch_x, batch_y = mnist.train.next_batch(batch_size)
      batch_x = batch_x.reshape((batch_size, n_steps, n_input))
      sess.run(optimizer, feed_dict={x: batch_x, y: batch_y})
      
      if step % display_step == 0:
         # Calculate batch accuracy
         acc = sess.run(accuracy, feed_dict={x: batch_x, y: batch_y})
         
         # Calculate batch loss
         loss = sess.run(cost, feed_dict={x: batch_x, y: batch_y})
         
         print("Iter " + str(step*batch_size) + ", Minibatch Loss= " + \
            "{:.6f}".format(loss) + ", Training Accuracy= " + \
            "{:.5f}".format(acc))
      step += 1
   print("Optimization Finished!")
      test_len = 128
   test_data = mnist.test.images[:test_len].reshape((-1, n_steps, n_input))
   
   test_label = mnist.test.labels[:test_len]
   print("Testing Accuracy:", \
      sess.run(accuracy, feed_dict={x: test_data, y: test_label}))

На скриншотах ниже показан сгенерированный результат —

TensorFlow — Визуализация TensorBoard

TensorFlow включает в себя инструмент визуализации, который называется TensorBoard. Он используется для анализа графика потока данных, а также для понимания моделей машинного обучения. Важная особенность TensorBoard включает в себя просмотр различных типов статистики о параметрах и деталях любого графика в вертикальном выравнивании.

Глубокая нейронная сеть включает до 36 000 узлов. TensorBoard помогает сворачивать эти узлы в блоки высокого уровня и выделять идентичные структуры. Это позволяет лучше анализировать граф, фокусируясь на основных разделах вычислительного графа. Говорят, что визуализация TensorBoard является очень интерактивной, где пользователь может перемещать, масштабировать и расширять узлы для отображения деталей.

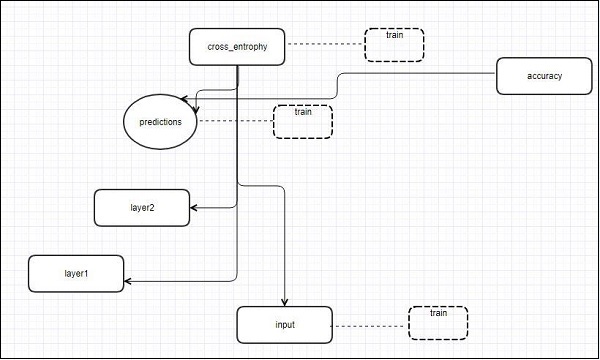
На следующем схематическом представлении показана полная работа визуализации TensorBoard:

Алгоритмы объединяют узлы в блоки высокого уровня и выделяют определенные группы с идентичными структурами, которые разделяют узлы высокого уровня. Созданная таким образом TensorBoard полезна и одинаково важна для настройки модели машинного обучения. Этот инструмент визуализации предназначен для файла журнала конфигурации со сводной информацией и подробностями, которые необходимо отобразить.

Давайте сосредоточимся на демонстрационном примере визуализации TensorBoard с помощью следующего кода:

import tensorflow as tf 

# Constants creation for TensorBoard visualization 
a = tf.constant(10,name = "a") 
b = tf.constant(90,name = "b") 
y = tf.Variable(a+b*2,name = 'y') 
model = tf.initialize_all_variables() #Creation of model 

with tf.Session() as session: 
   merged = tf.merge_all_summaries() 
   writer = tf.train.SummaryWriter("/tmp/tensorflowlogs",session.graph) 
   session.run(model) 
   print(session.run(y))

В следующей таблице показаны различные символы визуализации TensorBoard, используемые для представления узла.

TensorFlow — вложение слов

Вложение слова — это концепция отображения отдельных объектов, таких как слова, на векторы и действительные числа. Это важно для ввода для машинного обучения. Концепция включает в себя стандартные функции, которые эффективно преобразуют дискретные входные объекты в полезные векторы.

Пример ввода слов встраивания показан ниже:

blue: (0.01359, 0.00075997, 0.24608, ..., -0.2524, 1.0048, 0.06259)
blues: (0.01396, 0.11887, -0.48963, ..., 0.033483, -0.10007, 0.1158)
orange: (-0.24776, -0.12359, 0.20986, ..., 0.079717, 0.23865, -0.014213)
oranges: (-0.35609, 0.21854, 0.080944, ..., -0.35413, 0.38511, -0.070976)

Word2vec

Word2vec является наиболее распространенным подходом, используемым для неконтролируемой техники встраивания слов. Он обучает модель таким образом, что заданное входное слово предсказывает контекст слова с помощью скип-грамм.

TensorFlow позволяет реализовать множество способов реализации этой модели с повышением уровня сложности и оптимизации, а также с использованием концепций многопоточности и абстракций более высокого уровня.

import os 
import math 
import numpy as np 
import tensorflow as tf 

from tensorflow.contrib.tensorboard.plugins import projector 
batch_size = 64 
embedding_dimension = 5 
negative_samples = 8 
LOG_DIR = "logs/word2vec_intro" 

digit_to_word_map = {
   1: "One", 
   2: "Two", 
   3: "Three", 
   4: "Four", 
   5: "Five", 
   6: "Six", 
   7: "Seven", 
   8: "Eight", 
   9: "Nine"} 
sentences = [] 

# Create two kinds of sentences - sequences of odd and even digits. 
   for i in range(10000): 
   rand_odd_ints = np.random.choice(range(1, 10, 2), 3) 
      sentences.append(" ".join([digit_to_word_map[r] for r in rand_odd_ints])) 
   rand_even_ints = np.random.choice(range(2, 10, 2), 3) 
      sentences.append(" ".join([digit_to_word_map[r] for r in rand_even_ints])) 
   
# Map words to indices
word2index_map = {} 
index = 0 

for sent in sentences: 
   for word in sent.lower().split(): 
   
   if word not in word2index_map: 
      word2index_map[word] = index 
      index += 1 
index2word_map = {index: word for word, index in word2index_map.items()} 

vocabulary_size = len(index2word_map) 

# Generate skip-gram pairs 
skip_gram_pairs = [] 

for sent in sentences: 
   tokenized_sent = sent.lower().split() 
   
   for i in range(1, len(tokenized_sent)-1):        
      word_context_pair = [[word2index_map[tokenized_sent[i-1]], 
         word2index_map[tokenized_sent[i+1]]], word2index_map[tokenized_sent[i]]] 
      
      skip_gram_pairs.append([word_context_pair[1], word_context_pair[0][0]]) 
      skip_gram_pairs.append([word_context_pair[1], word_context_pair[0][1]]) 

def get_skipgram_batch(batch_size): 
   instance_indices = list(range(len(skip_gram_pairs))) 
      np.random.shuffle(instance_indices)
   batch = instance_indices[:batch_size] 
   x = [skip_gram_pairs[i][0] for i in batch] 
   y = [[skip_gram_pairs[i][1]] for i in batch] 
   return x, y 
   
# batch example 
x_batch, y_batch = get_skipgram_batch(8) 
x_batch 
y_batch 
[index2word_map[word] for word in x_batch] [index2word_map[word[0]] for word in y_batch] 

# Input data, labels train_inputs = tf.placeholder(tf.int32, shape = [batch_size]) 
   train_labels = tf.placeholder(tf.int32, shape = [batch_size, 1]) 

# Embedding lookup table currently only implemented in CPU with 
   tf.name_scope("embeddings"): 
   embeddings = tf.Variable(    
      tf.random_uniform([vocabulary_size, embedding_dimension], -1.0, 1.0), 
         name = 'embedding') 
   # This is essentialy a lookup table 
   embed = tf.nn.embedding_lookup(embeddings, train_inputs) 
   
# Create variables for the NCE loss
nce_weights = tf.Variable(     
   tf.truncated_normal([vocabulary_size, embedding_dimension], stddev = 1.0 / 
      math.sqrt(embedding_dimension))) 
   
nce_biases = tf.Variable(tf.zeros([vocabulary_size])) 

loss = tf.reduce_mean(     
   tf.nn.nce_loss(weights = nce_weights, biases = nce_biases, inputs = embed, 
   labels = train_labels,num_sampled = negative_samples, 
   num_classes = vocabulary_size)) tf.summary.scalar("NCE_loss", loss) 
   
# Learning rate decay 
global_step = tf.Variable(0, trainable = False) 
   learningRate = tf.train.exponential_decay(learning_rate = 0.1, 
   global_step = global_step, decay_steps = 1000, decay_rate = 0.95, staircase = True) 

train_step = tf.train.GradientDescentOptimizer(learningRate).minimize(loss) 
   merged = tf.summary.merge_all() 
with tf.Session() as sess: 
   train_writer = tf.summary.FileWriter(LOG_DIR,    
      graph = tf.get_default_graph()) 
   saver = tf.train.Saver() 
   
   with open(os.path.join(LOG_DIR, 'metadata.tsv'), "w") as metadata: 
      metadata.write('Name\tClass\n') for k, v in index2word_map.items(): 
      metadata.write('%s\t%d\n' % (v, k)) 
   
   config = projector.ProjectorConfig() 
   embedding = config.embeddings.add() embedding.tensor_name = embeddings.name 
   
   # Link this tensor to its metadata file (e.g. labels). 
   embedding.metadata_path = os.path.join(LOG_DIR, 'metadata.tsv') 
      projector.visualize_embeddings(train_writer, config) 
   
   tf.global_variables_initializer().run() 
   
   for step in range(1000): 
      x_batch, y_batch = get_skipgram_batch(batch_size) summary, _ = sess.run(
         [merged, train_step], feed_dict = {train_inputs: x_batch, train_labels: y_batch})
      train_writer.add_summary(summary, step)
      
      if step % 100 == 0:
         saver.save(sess, os.path.join(LOG_DIR, "w2v_model.ckpt"), step)
         loss_value = sess.run(loss, feed_dict = {
            train_inputs: x_batch, train_labels: y_batch})
         print("Loss at %d: %.5f" % (step, loss_value))

   # Normalize embeddings before using
   norm = tf.sqrt(tf.reduce_sum(tf.square(embeddings), 1, keep_dims = True))
   normalized_embeddings = embeddings /
      norm normalized_embeddings_matrix = sess.run(normalized_embeddings)
   
ref_word = normalized_embeddings_matrix[word2index_map["one"]]

cosine_dists = np.dot(normalized_embeddings_matrix, ref_word)
ff = np.argsort(cosine_dists)[::-1][1:10] for f in ff: print(index2word_map[f])
print(cosine_dists[f])

Выход

Приведенный выше код генерирует следующий вывод —

TensorFlow — однослойный персептрон

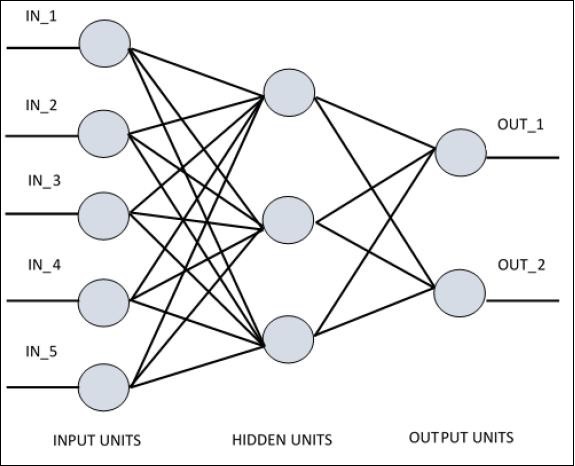
Для понимания однослойного персептрона важно понимать Искусственные Нейронные Сети (ANN). Искусственные нейронные сети — это система обработки информации, механизм которой вдохновлен функциональностью биологических нейронных цепей. Искусственная нейронная сеть обладает множеством процессорных блоков, связанных друг с другом. Ниже приводится схематическое изображение искусственной нейронной сети —

Диаграмма показывает, что скрытые блоки связываются с внешним слоем. При этом блоки ввода и вывода обмениваются данными только через скрытый слой сети.

Схема связи с узлами, общее количество слоев и уровень узлов между входами и выходами с количеством нейронов на слой определяют архитектуру нейронной сети.

Есть два типа архитектуры. Эти типы ориентированы на функциональность искусственных нейронных сетей следующим образом:

Однослойный персептрон
Многослойный персептрон

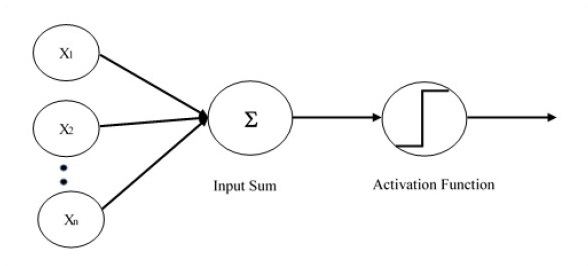
Однослойный персептрон

Однослойный персептрон — первая предложенная нейронная модель. Содержимое локальной памяти нейрона состоит из вектора весов. Вычисление однослойного персептрона выполняется по вычислению суммы входного вектора, каждое со значением, умноженным на соответствующий элемент вектора весов. Значение, которое отображается на выходе, будет входом функции активации.

Давайте сосредоточимся на реализации однослойного персептрона для задачи классификации изображений с использованием TensorFlow. Наилучшим примером для иллюстрации однослойного персептрона является представление «логистической регрессии».

Теперь рассмотрим следующие основные этапы обучения логистической регрессии —

Веса инициализируются случайными значениями в начале тренировки.
Для каждого элемента обучающего набора ошибка рассчитывается с разницей между желаемым выходом и фактическим выходом. Рассчитанная ошибка используется для корректировки весов.
Процесс повторяется до тех пор, пока ошибка, допущенная во всем обучающем наборе, не станет меньше указанного порогового значения, пока не будет достигнуто максимальное количество итераций.

Веса инициализируются случайными значениями в начале тренировки.

Для каждого элемента обучающего набора ошибка рассчитывается с разницей между желаемым выходом и фактическим выходом. Рассчитанная ошибка используется для корректировки весов.

Процесс повторяется до тех пор, пока ошибка, допущенная во всем обучающем наборе, не станет меньше указанного порогового значения, пока не будет достигнуто максимальное количество итераций.

Полный код для оценки логистической регрессии упомянут ниже:

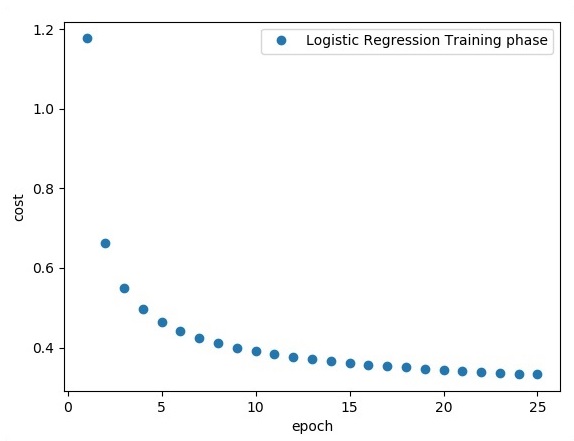
# Import MINST data 
from tensorflow.examples.tutorials.mnist import input_data 
mnist = input_data.read_data_sets("/tmp/data/", one_hot = True) 

import tensorflow as tf 
import matplotlib.pyplot as plt 

# Parameters 
learning_rate = 0.01 
training_epochs = 25 
batch_size = 100 
display_step = 1 

# tf Graph Input 
x = tf.placeholder("float", [None, 784]) # mnist data image of shape 28*28 = 784 
y = tf.placeholder("float", [None, 10]) # 0-9 digits recognition => 10 classes 

# Create model 
# Set model weights 
W = tf.Variable(tf.zeros([784, 10])) 
b = tf.Variable(tf.zeros([10])) 

# Construct model 
activation = tf.nn.softmax(tf.matmul(x, W) + b) # Softmax 

# Minimize error using cross entropy 
cross_entropy = y*tf.log(activation) 
cost = tf.reduce_mean\ (-tf.reduce_sum\ (cross_entropy,reduction_indices = 1)) 

optimizer = tf.train.\ GradientDescentOptimizer(learning_rate).minimize(cost) 

#Plot settings 
avg_set = [] 
epoch_set = [] 

# Initializing the variables init = tf.initialize_all_variables()
# Launch the graph 
with tf.Session() as sess:
   sess.run(init)
   
   # Training cycle
   for epoch in range(training_epochs):
      avg_cost = 0.
      total_batch = int(mnist.train.num_examples/batch_size)
      
      # Loop over all batches
      for i in range(total_batch):
         batch_xs, batch_ys = \ mnist.train.next_batch(batch_size)
         # Fit training using batch data sess.run(optimizer, \ feed_dict = {
            x: batch_xs, y: batch_ys}) 
         # Compute average loss avg_cost += sess.run(cost, \ feed_dict = {
            x: batch_xs, \ y: batch_ys})/total_batch
      # Display logs per epoch step
      if epoch % display_step == 0:
         print ("Epoch:", '%04d' % (epoch+1), "cost=", "{:.9f}".format(avg_cost))
            avg_set.append(avg_cost) epoch_set.append(epoch+1)
   print ("Training phase finished")
    
   plt.plot(epoch_set,avg_set, 'o', label = 'Logistic Regression Training phase') 
   plt.ylabel('cost') 
   plt.xlabel('epoch') 
   plt.legend() 
   plt.show() 
    
   # Test model 
   correct_prediction = tf.equal(tf.argmax(activation, 1), tf.argmax(y, 1)) 
   
   # Calculate accuracy 
   accuracy = tf.reduce_mean(tf.cast(correct_prediction, "float")) print 
      ("Model accuracy:", accuracy.eval({x: mnist.test.images, y: mnist.test.labels}))

Выход

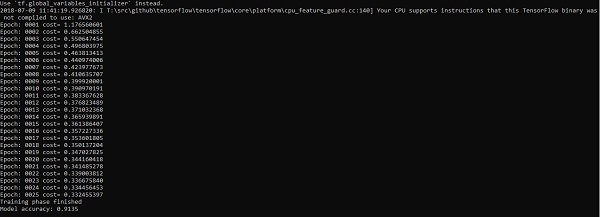
Приведенный выше код генерирует следующий вывод —

Логистическая регрессия рассматривается как прогнозный анализ. Логистическая регрессия используется для описания данных и объяснения взаимосвязи между одной зависимой двоичной переменной и одной или несколькими номинальными или независимыми переменными.

TensorFlow — Линейная регрессия

В этой главе мы сосредоточимся на базовом примере реализации линейной регрессии с использованием TensorFlow. Логистическая регрессия или линейная регрессия — это контролируемый подход машинного обучения для классификации категорий дискретных порядков. Наша цель в этой главе — создать модель, с помощью которой пользователь может предсказать взаимосвязь между переменными предиктора и одной или несколькими независимыми переменными.

Соотношение между этими двумя переменными считается линейным. Если y является зависимой переменной, а x рассматривается как независимая переменная, то отношение линейной регрессии двух переменных будет выглядеть следующим образом:

Y = Ax+b

Мы разработаем алгоритм для линейной регрессии. Это позволит нам понять следующие два важных понятия —

Функция стоимости
Алгоритмы градиентного спуска

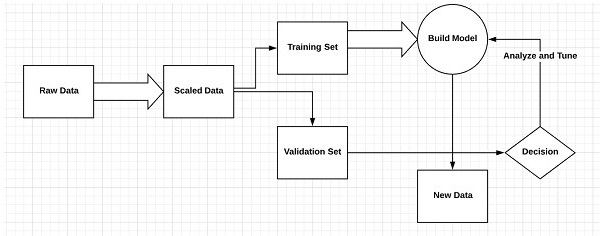
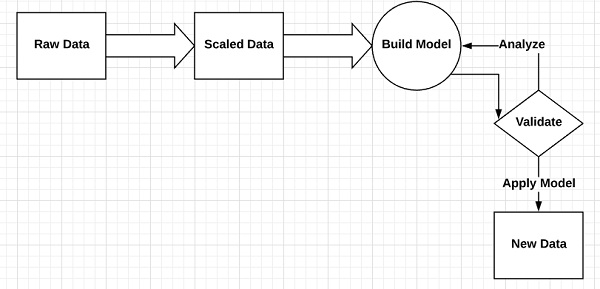
Схематическое представление линейной регрессии упоминается ниже —

Графическое представление уравнения линейной регрессии упоминается ниже —

Шаги по разработке алгоритма линейной регрессии

Теперь мы узнаем о шагах, которые помогают в разработке алгоритма линейной регрессии.

Шаг 1

Важно импортировать необходимые модули для построения модуля линейной регрессии. Мы начинаем импортировать библиотеки Python NumPy и Matplotlib.

import numpy as np 
import matplotlib.pyplot as plt

Шаг 2

Определите количество коэффициентов, необходимых для логистической регрессии.

number_of_points = 500 
x_point = [] 
y_point = [] 
a = 0.22 
b = 0.78

Шаг 3

Итерация переменных для генерации 300 случайных точек вокруг уравнения регрессии —

Y = 0,22x + 0,78

for i in range(number_of_points): 
   x = np.random.normal(0.0,0.5) 
   y = a*x + b +np.random.normal(0.0,0.1) x_point.append([x]) 
   y_point.append([y])

Шаг 4

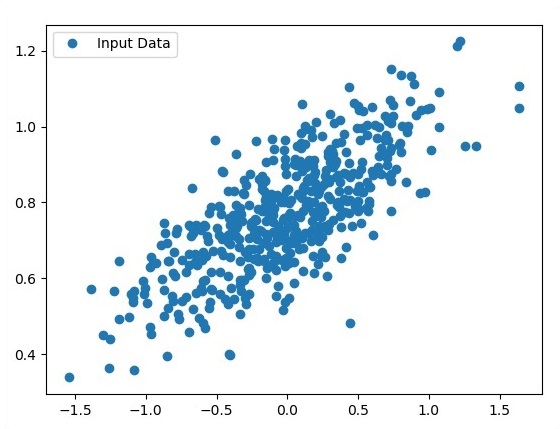
Просмотр сгенерированных точек с помощью Matplotlib.

fplt.plot(x_point,y_point, 'o', label = 'Input Data') plt.legend() plt.show()

Полный код логистической регрессии выглядит следующим образом:

import numpy as np 
import matplotlib.pyplot as plt 

number_of_points = 500 
x_point = [] 
y_point = [] 
a = 0.22 
b = 0.78 

for i in range(number_of_points): 
   x = np.random.normal(0.0,0.5) 
   y = a*x + b +np.random.normal(0.0,0.1) x_point.append([x]) 
   y_point.append([y]) 
   
plt.plot(x_point,y_point, 'o', label = 'Input Data') plt.legend() 
plt.show()

Количество точек, которое берется в качестве входных данных, считается входными данными.

TensorFlow — TFLearn и его установка

TFLearn может быть определен как модульный и прозрачный аспект глубокого обучения, используемый в платформе TensorFlow. Основным мотивом TFLearn является предоставление API TensorFlow более высокого уровня для облегчения и демонстрации новых экспериментов.

Рассмотрим следующие важные особенности TFLearn —

TFLearn прост в использовании и понимании.
Он включает в себя простые концепции для построения высокомодульных сетевых уровней, оптимизаторов и различных метрик, встроенных в них.
Включает полную прозрачность с системой работы TensorFlow.
Он включает в себя мощные вспомогательные функции для обучения встроенных тензоров, которые принимают несколько входов, выходов и оптимизаторов.
Он включает в себя простую и красивую визуализацию графика.
Визуализация графика включает в себя различные детали весов, градиентов и активаций.

TFLearn прост в использовании и понимании.

Он включает в себя простые концепции для построения высокомодульных сетевых уровней, оптимизаторов и различных метрик, встроенных в них.

Включает полную прозрачность с системой работы TensorFlow.

Он включает в себя мощные вспомогательные функции для обучения встроенных тензоров, которые принимают несколько входов, выходов и оптимизаторов.

Он включает в себя простую и красивую визуализацию графика.

Визуализация графика включает в себя различные детали весов, градиентов и активаций.

Установите TFLearn, выполнив следующую команду —

pip install tflearn

После выполнения кода выше будет сгенерирован следующий вывод:

На следующем рисунке показана реализация TFLearn с классификатором Random Forest —

from __future__ import division, print_function, absolute_import

#TFLearn module implementation
import tflearn
from tflearn.estimators import RandomForestClassifier

# Data loading and pre-processing with respect to dataset
import tflearn.datasets.mnist as mnist
X, Y, testX, testY = mnist.load_data(one_hot = False)

m = RandomForestClassifier(n_estimators = 100, max_nodes = 1000)
m.fit(X, Y, batch_size = 10000, display_step = 10)

print("Compute the accuracy on train data:")
print(m.evaluate(X, Y, tflearn.accuracy_op))

print("Compute the accuracy on test set:")
print(m.evaluate(testX, testY, tflearn.accuracy_op))

print("Digits for test images id 0 to 5:")
print(m.predict(testX[:5]))

print("True digits:")
print(testY[:5])

TensorFlow — разница CNN и RNN

В этой главе мы сосредоточимся на разнице между CNN и RNN —

CNN	РНН
Он подходит для пространственных данных, таких как изображения.	RNN подходит для временных данных, также называемых последовательными данными.
CNN считается более мощным, чем RNN.	RNN включает меньшую совместимость функций по сравнению с CNN.
Эта сеть принимает входы фиксированного размера и генерирует выходы фиксированного размера.	RNN может обрабатывать произвольные длины ввода / вывода.
CNN — это тип искусственной нейронной сети с прямой связью с вариациями многослойных персептронов, предназначенных для использования минимальных объемов предварительной обработки.	RNN в отличие от нейронных сетей прямой связи — может использовать свою внутреннюю память для обработки произвольных последовательностей входных данных.
CNN используют схему связи между нейронами. Это вдохновлено организацией зрительной коры животных, отдельные нейроны которой расположены таким образом, что они реагируют на перекрывающиеся области, покрывающие зрительное поле.	Периодические нейронные сети используют информацию временных рядов — то, что пользователь говорил последним, повлияет на то, что он / она скажет дальше.
CNN идеальны для обработки изображений и видео.	RNN идеально подходят для анализа текста и речи.

Следующая иллюстрация показывает схематическое представление CNN и RNN —

Тензорфлоу — Керас

Keras — это компактная, простая в изучении высокоуровневая библиотека Python, работающая поверх фреймворка TensorFlow. Это сделано с акцентом на понимание методов глубокого обучения, таких как создание слоев для нейронных сетей, поддерживающих концепции форм и математических деталей. Создание freamework может быть следующих двух типов —

Последовательный API
Функциональный API

Рассмотрим следующие восемь шагов для создания модели глубокого обучения в Керасе:

Загрузка данных
Предварительная обработка загруженных данных
Определение модели
Компиляция модели
Подходит указанная модель
Оцените это
Сделайте необходимые прогнозы
Сохранить модель

Мы будем использовать блокнот Jupyter для выполнения и отображения вывода, как показано ниже —

Шаг 1 — Загрузка данных и предварительная обработка загруженных данных осуществляются первыми для выполнения модели глубокого обучения.

import warnings
warnings.filterwarnings('ignore')

import numpy as np
np.random.seed(123) # for reproducibility

from keras.models import Sequential
from keras.layers import Flatten, MaxPool2D, Conv2D, Dense, Reshape, Dropout
from keras.utils import np_utils
Using TensorFlow backend.
from keras.datasets import mnist

# Load pre-shuffled MNIST data into train and test sets
(X_train, y_train), (X_test, y_test) = mnist.load_data()
X_train = X_train.reshape(X_train.shape[0], 28, 28, 1)
X_test = X_test.reshape(X_test.shape[0], 28, 28, 1)
X_train = X_train.astype('float32')
X_test = X_test.astype('float32')
X_train /= 255
X_test /= 255
Y_train = np_utils.to_categorical(y_train, 10)
Y_test = np_utils.to_categorical(y_test, 10)

Этот шаг может быть определен как «Импорт библиотек и модулей», что означает, что все библиотеки и модули импортируются как начальный шаг.

Шаг 2 — На этом шаге мы определим архитектуру модели —

model = Sequential()
model.add(Conv2D(32, 3, 3, activation = 'relu', input_shape = (28,28,1)))
model.add(Conv2D(32, 3, 3, activation = 'relu'))
model.add(MaxPool2D(pool_size = (2,2)))
model.add(Dropout(0.25))
model.add(Flatten())
model.add(Dense(128, activation = 'relu'))
model.add(Dropout(0.5))
model.add(Dense(10, activation = 'softmax'))

Шаг 3 — Давайте теперь скомпилируем указанную модель —

model.compile(loss = 'categorical_crossentropy', optimizer = 'adam', metrics = ['accuracy'])

Шаг 4 — Теперь мы подгоним модель, используя данные обучения —

model.fit(X_train, Y_train, batch_size = 32, epochs = 10, verbose = 1)

Вывод созданных итераций выглядит следующим образом:

Epoch 1/10 60000/60000 [==============================] - 65s - 
loss: 0.2124 - 
acc: 0.9345 
Epoch 2/10 60000/60000 [==============================] - 62s - 
loss: 0.0893 - 
acc: 0.9740 
Epoch 3/10 60000/60000 [==============================] - 58s - 
loss: 0.0665 - 
acc: 0.9802 
Epoch 4/10 60000/60000 [==============================] - 62s - 
loss: 0.0571 - 
acc: 0.9830 
Epoch 5/10 60000/60000 [==============================] - 62s - 
loss: 0.0474 - 
acc: 0.9855 
Epoch 6/10 60000/60000 [==============================] - 59s -
loss: 0.0416 - 
acc: 0.9871 
Epoch 7/10 60000/60000 [==============================] - 61s - 
loss: 0.0380 - 
acc: 0.9877 
Epoch 8/10 60000/60000 [==============================] - 63s - 
loss: 0.0333 - 
acc: 0.9895 
Epoch 9/10 60000/60000 [==============================] - 64s - 
loss: 0.0325 - 
acc: 0.9898 
Epoch 10/10 60000/60000 [==============================] - 60s - 
loss: 0.0284 - 
acc: 0.9910

TensorFlow — распределенные вычисления

Эта глава будет посвящена тому, как начать работу с распределенным TensorFlow. Цель состоит в том, чтобы помочь разработчикам понять основные концепции распределенных TF, которые повторяются, такие как TF-серверы. Мы будем использовать Блокнот Jupyter для оценки распределенного TensorFlow. Реализация распределенных вычислений с TensorFlow упоминается ниже —

Шаг 1 — Импорт необходимых модулей, обязательных для распределенных вычислений —

import tensorflow as tf

Шаг 2 — Создайте кластер TensorFlow с одним узлом. Пусть этот узел будет отвечать за задание с именем «работник», которое будет выполнять один дубль на локальном узле: 2222.

cluster_spec = tf.train.ClusterSpec({'worker' : ['localhost:2222']})
server = tf.train.Server(cluster_spec)
server.target

Вышеуказанные сценарии генерируют следующий вывод —

'grpc://localhost:2222'
The server is currently running.

Шаг 3 — Конфигурация сервера с соответствующим сеансом может быть рассчитана с помощью следующей команды:

server.server_def

Приведенная выше команда генерирует следующий вывод —

cluster {
   job {
      name: "worker"
      tasks {
         value: "localhost:2222"
      }
   }
}
job_name: "worker"
protocol: "grpc"

Шаг 4 — Запустите сеанс TensorFlow с сервером выполнения, являющимся сервером. Используйте TensorFlow для создания локального сервера и используйте lsof, чтобы узнать местоположение сервера.

sess = tf.Session(target = server.target)
server = tf.train.Server.create_local_server()

Шаг 5 — Просмотрите устройства, доступные в этом сеансе, и закройте соответствующий сеанс.

devices = sess.list_devices()
for d in devices:
   print(d.name)
sess.close()

Приведенная выше команда генерирует следующий вывод —

/job:worker/replica:0/task:0/device:CPU:0

TensorFlow — Экспорт

Здесь мы сосредоточимся на формировании MetaGraph в TensorFlow. Это поможет нам понять модуль экспорта в TensorFlow. MetaGraph содержит основную информацию, необходимую для обучения, выполнения оценки или выполнения вывода на ранее обученном графике.

Ниже приведен фрагмент кода для того же —

def export_meta_graph(filename = None, collection_list = None, as_text = False): 
   """this code writes `MetaGraphDef` to save_path/filename. 
   
   Arguments: 
   filename: Optional meta_graph filename including the path. collection_list: 
      List of string keys to collect. as_text: If `True`, 
      writes the meta_graph as an ASCII proto. 
   
   Returns: 
   A `MetaGraphDef` proto. """

Одна из типичных моделей использования того же самого упомянута ниже —

# Build the model ... 
with tf.Session() as sess: 
   # Use the model ... 
# Export the model to /tmp/my-model.meta. 
meta_graph_def = tf.train.export_meta_graph(filename = '/tmp/my-model.meta')

TensorFlow — многослойное обучение персептрону

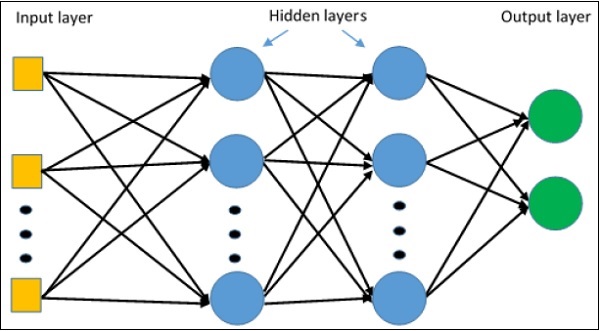
Многослойный персептрон определяет наиболее сложную архитектуру искусственных нейронных сетей. Он в основном состоит из нескольких слоев персептрона.

Схематическое представление многослойного обучения персептрона показано ниже:

Сети MLP обычно используются в контролируемом формате обучения. Типичный алгоритм обучения для сетей MLP также называется алгоритмом обратного распространения.

Теперь мы сосредоточимся на реализации с MLP для проблемы классификации изображений.

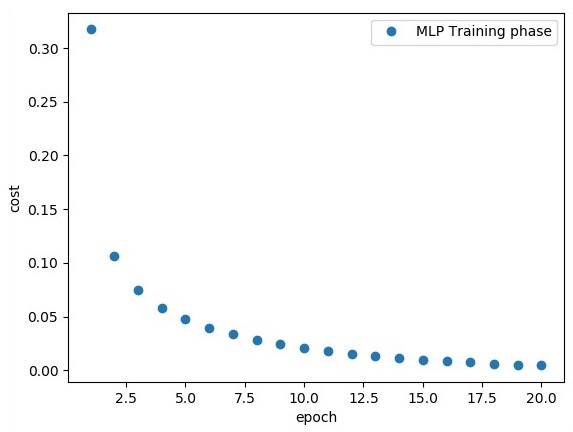
# Import MINST data 
from tensorflow.examples.tutorials.mnist import input_data 
mnist = input_data.read_data_sets("/tmp/data/", one_hot = True) 

import tensorflow as tf 
import matplotlib.pyplot as plt 

# Parameters 
learning_rate = 0.001 
training_epochs = 20 
batch_size = 100 
display_step = 1 

# Network Parameters 
n_hidden_1 = 256 

# 1st layer num features
n_hidden_2 = 256 # 2nd layer num features 
n_input = 784 # MNIST data input (img shape: 28*28) n_classes = 10 
# MNIST total classes (0-9 digits) 

# tf Graph input 
x = tf.placeholder("float", [None, n_input]) 
y = tf.placeholder("float", [None, n_classes]) 

# weights layer 1 
h = tf.Variable(tf.random_normal([n_input, n_hidden_1])) # bias layer 1 
bias_layer_1 = tf.Variable(tf.random_normal([n_hidden_1])) 
# layer 1 layer_1 = tf.nn.sigmoid(tf.add(tf.matmul(x, h), bias_layer_1)) 

# weights layer 2 
w = tf.Variable(tf.random_normal([n_hidden_1, n_hidden_2])) 

# bias layer 2 
bias_layer_2 = tf.Variable(tf.random_normal([n_hidden_2])) 

# layer 2 
layer_2 = tf.nn.sigmoid(tf.add(tf.matmul(layer_1, w), bias_layer_2)) 

# weights output layer 
output = tf.Variable(tf.random_normal([n_hidden_2, n_classes])) 

# biar output layer 
bias_output = tf.Variable(tf.random_normal([n_classes])) # output layer 
output_layer = tf.matmul(layer_2, output) + bias_output

# cost function 
cost = tf.reduce_mean(tf.nn.sigmoid_cross_entropy_with_logits(
   logits = output_layer, labels = y)) 

#cost = tf.reduce_mean(tf.nn.sigmoid_cross_entropy_with_logits(output_layer, y)) 
# optimizer 
optimizer = tf.train.AdamOptimizer(learning_rate = learning_rate).minimize(cost) 

# optimizer = tf.train.GradientDescentOptimizer(
   learning_rate = learning_rate).minimize(cost) 

# Plot settings 
avg_set = [] 
epoch_set = [] 

# Initializing the variables 
init = tf.global_variables_initializer() 

# Launch the graph 
with tf.Session() as sess: 
   sess.run(init) 
   
   # Training cycle
   for epoch in range(training_epochs): 
      avg_cost = 0. 
      total_batch = int(mnist.train.num_examples / batch_size) 
      
      # Loop over all batches 
      for i in range(total_batch): 
         batch_xs, batch_ys = mnist.train.next_batch(batch_size) 
         # Fit training using batch data sess.run(optimizer, feed_dict = {
            x: batch_xs, y: batch_ys}) 
         # Compute average loss 
         avg_cost += sess.run(cost, feed_dict = {x: batch_xs, y: batch_ys}) / total_batch
      # Display logs per epoch step 
      if epoch % display_step == 0: 
         print 
         Epoch:", '%04d' % (epoch + 1), "cost=", "{:.9f}".format(avg_cost)
      avg_set.append(avg_cost) 
      epoch_set.append(epoch + 1)
   print 
   "Training phase finished" 
   
   plt.plot(epoch_set, avg_set, 'o', label = 'MLP Training phase') 
   plt.ylabel('cost') 
   plt.xlabel('epoch') 
   plt.legend() 
   plt.show() 
   
   # Test model 
   correct_prediction = tf.equal(tf.argmax(output_layer, 1), tf.argmax(y, 1)) 
   
   # Calculate accuracy 
   accuracy = tf.reduce_mean(tf.cast(correct_prediction, "float")) 
   print 
   "Model Accuracy:", accuracy.eval({x: mnist.test.images, y: mnist.test.labels})

Выше строка кода генерирует следующий вывод —

TensorFlow — скрытые слои персептрона

В этой главе мы сосредоточимся на сети, которую нам нужно будет изучить из известного набора точек, называемых x и f (x). Один скрытый слой создаст эту простую сеть.

Код для объяснения скрытых слоев персептрона, как показано ниже —

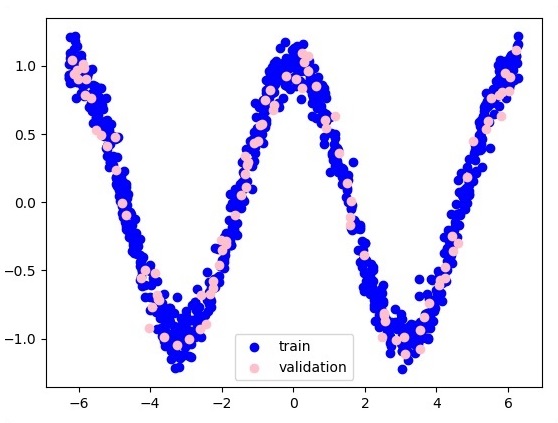
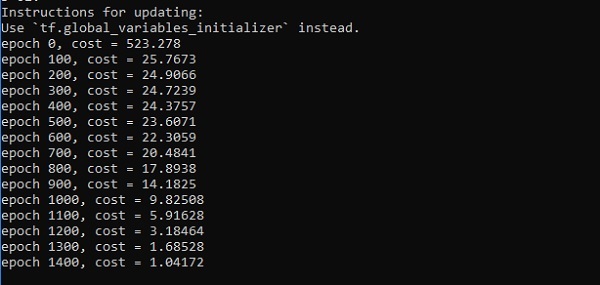
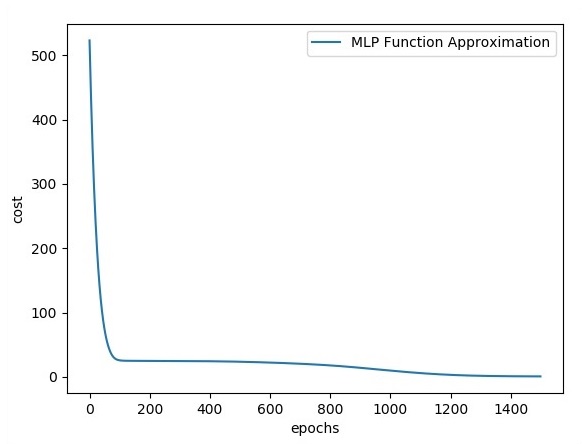
#Importing the necessary modules 
import tensorflow as tf 
import numpy as np 
import math, random 
import matplotlib.pyplot as plt 

np.random.seed(1000) 
function_to_learn = lambda x: np.cos(x) + 0.1*np.random.randn(*x.shape) 
layer_1_neurons = 10 
NUM_points = 1000 

#Training the parameters 
batch_size = 100 
NUM_EPOCHS = 1500 

all_x = np.float32(np.random.uniform(-2*math.pi, 2*math.pi, (1, NUM_points))).T 
   np.random.shuffle(all_x) 

train_size = int(900) 
#Training the first 700 points in the given set x_training = all_x[:train_size] 
y_training = function_to_learn(x_training)

#Training the last 300 points in the given set x_validation = all_x[train_size:] 
y_validation = function_to_learn(x_validation) 

plt.figure(1) 
plt.scatter(x_training, y_training, c = 'blue', label = 'train') 
plt.scatter(x_validation, y_validation, c = 'pink', label = 'validation') 
plt.legend() 
plt.show()

X = tf.placeholder(tf.float32, [None, 1], name = "X")
Y = tf.placeholder(tf.float32, [None, 1], name = "Y")

#first layer 
#Number of neurons = 10 
w_h = tf.Variable(
   tf.random_uniform([1, layer_1_neurons],\ minval = -1, maxval = 1, dtype = tf.float32)) 
b_h = tf.Variable(tf.zeros([1, layer_1_neurons], dtype = tf.float32)) 
h = tf.nn.sigmoid(tf.matmul(X, w_h) + b_h)

#output layer 
#Number of neurons = 10 
w_o = tf.Variable(
   tf.random_uniform([layer_1_neurons, 1],\ minval = -1, maxval = 1, dtype = tf.float32)) 
b_o = tf.Variable(tf.zeros([1, 1], dtype = tf.float32)) 

#build the model 
model = tf.matmul(h, w_o) + b_o 

#minimize the cost function (model - Y) 
train_op = tf.train.AdamOptimizer().minimize(tf.nn.l2_loss(model - Y)) 

#Start the Learning phase 
sess = tf.Session() sess.run(tf.initialize_all_variables()) 

errors = [] 
for i in range(NUM_EPOCHS): 
   for start, end in zip(range(0, len(x_training), batch_size),\ 
      range(batch_size, len(x_training), batch_size)): 
      sess.run(train_op, feed_dict = {X: x_training[start:end],\ Y: y_training[start:end]})
   cost = sess.run(tf.nn.l2_loss(model - y_validation),\ feed_dict = {X:x_validation}) 
   errors.append(cost) 
   
   if i%100 == 0: 
      print("epoch %d, cost = %g" % (i, cost)) 
      
plt.plot(errors,label='MLP Function Approximation') plt.xlabel('epochs') 
plt.ylabel('cost') 
plt.legend() 
plt.show()

Выход

Ниже приводится представление приближения функционального слоя —

Здесь два данных представлены в форме буквы W. Два данных: поезд и проверка, которые представлены разными цветами, как видно в разделе легенды.

TensorFlow — оптимизаторы

Оптимизаторы — это расширенный класс, который включает дополнительную информацию для обучения конкретной модели. Класс оптимизатора инициализируется с заданными параметрами, но важно помнить, что тензор не нужен. Оптимизаторы используются для повышения скорости и производительности при обучении конкретной модели.

Основной оптимизатор TensorFlow — это

tf.train.Optimizer

Этот класс определен в указанном пути файла tenorflow / python / training / optimizer.py.

Ниже приведены некоторые оптимизаторы в Tensorflow —

Стохастический градиентный спуск
Стохастический градиентный спуск с градиентным отсечением
инерция
Нестеров импульс
Adagrad
Adadelta
RMSProp
Адам
Adamax
SMORMS3

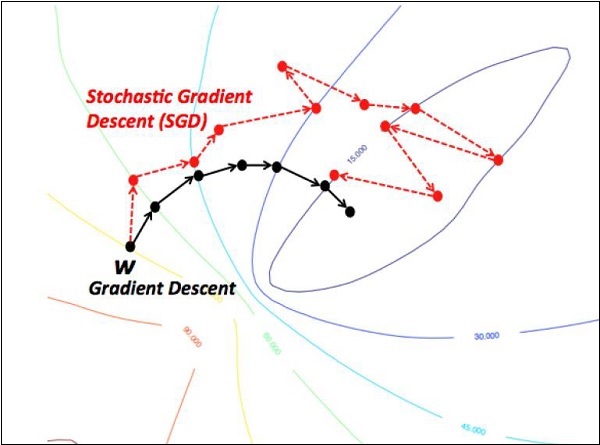
Мы сосредоточимся на стохастическом градиентном спуске. Иллюстрация для создания оптимизатора для того же самого упомянута ниже —

def sgd(cost, params, lr = np.float32(0.01)):
   g_params = tf.gradients(cost, params)
   updates = []
   
   for param, g_param in zip(params, g_params):
      updates.append(param.assign(param - lr*g_param))
   return updates

Основные параметры определены в конкретной функции. В нашей следующей главе мы сосредоточимся на оптимизации градиентного спуска с использованием оптимизаторов.

TensorFlow — реализация XOR

В этой главе мы узнаем о реализации XOR с использованием TensorFlow. Прежде чем начать с реализации XOR в TensorFlow, давайте посмотрим значения таблицы XOR. Это поможет нам понять процесс шифрования и дешифрования.

	В	A XOR B
0	0	0
0	1	1
1	0	1
1	1	0

Метод шифрования XOR в основном используется для шифрования данных, которые трудно взломать методом грубой силы, т. Е. Путем генерации случайных ключей шифрования, которые соответствуют соответствующему ключу.

Концепция реализации с XOR Cipher состоит в том, чтобы определить ключ шифрования XOR и затем выполнить операцию XOR символов в указанной строке с этим ключом, который пользователь пытается зашифровать. Теперь мы сосредоточимся на реализации XOR с использованием TensorFlow, которая упоминается ниже —

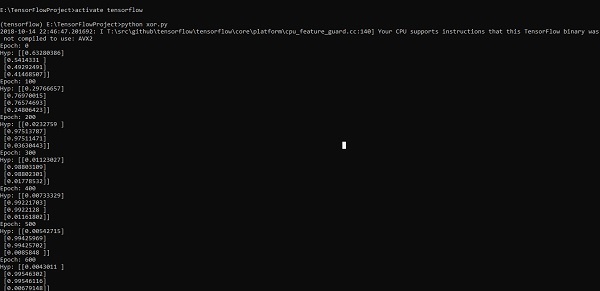
#Declaring necessary modules
import tensorflow as tf
import numpy as np
"""
A simple numpy implementation of a XOR gate to understand the backpropagation
algorithm
"""

x = tf.placeholder(tf.float64,shape = [4,2],name = "x")
#declaring a place holder for input x
y = tf.placeholder(tf.float64,shape = [4,1],name = "y")
#declaring a place holder for desired output y

m = np.shape(x)[0]#number of training examples
n = np.shape(x)[1]#number of features
hidden_s = 2 #number of nodes in the hidden layer
l_r = 1#learning rate initialization

theta1 = tf.cast(tf.Variable(tf.random_normal([3,hidden_s]),name = "theta1"),tf.float64)
theta2 = tf.cast(tf.Variable(tf.random_normal([hidden_s+1,1]),name = "theta2"),tf.float64)

#conducting forward propagation
a1 = tf.concat([np.c_[np.ones(x.shape[0])],x],1)
#the weights of the first layer are multiplied by the input of the first layer

z1 = tf.matmul(a1,theta1)
#the input of the second layer is the output of the first layer, passed through the 
   activation function and column of biases is added

a2 = tf.concat([np.c_[np.ones(x.shape[0])],tf.sigmoid(z1)],1)
#the input of the second layer is multiplied by the weights

z3 = tf.matmul(a2,theta2)
#the output is passed through the activation function to obtain the final probability

h3 = tf.sigmoid(z3)
cost_func = -tf.reduce_sum(y*tf.log(h3)+(1-y)*tf.log(1-h3),axis = 1)

#built in tensorflow optimizer that conducts gradient descent using specified 
   learning rate to obtain theta values

optimiser = tf.train.GradientDescentOptimizer(learning_rate = l_r).minimize(cost_func)

#setting required X and Y values to perform XOR operation
X = [[0,0],[0,1],[1,0],[1,1]]
Y = [[0],[1],[1],[0]]

#initializing all variables, creating a session and running a tensorflow session
init = tf.global_variables_initializer()
sess = tf.Session()
sess.run(init)

#running gradient descent for each iteration and printing the hypothesis 
   obtained using the updated theta values
for i in range(100000):
   sess.run(optimiser, feed_dict = {x:X,y:Y})#setting place holder values using feed_dict
   if i%100==0:
      print("Epoch:",i)
      print("Hyp:",sess.run(h3,feed_dict = {x:X,y:Y}))

Выше строка кода генерирует вывод, как показано на скриншоте ниже —

TensorFlow — Оптимизация градиентного спуска

Оптимизация градиентного спуска считается важной концепцией в науке о данных.

Рассмотрим шаги, показанные ниже, чтобы понять реализацию оптимизации градиентного спуска —

Шаг 1

Включите необходимые модули и объявление переменных x и y, с помощью которых мы собираемся определить оптимизацию градиентного спуска.

import tensorflow as tf

x = tf.Variable(2, name = 'x', dtype = tf.float32)
log_x = tf.log(x)
log_x_squared = tf.square(log_x)

optimizer = tf.train.GradientDescentOptimizer(0.5)
train = optimizer.minimize(log_x_squared)

Шаг 2

Инициализируйте необходимые переменные и вызовите оптимизаторы для определения и вызова их с соответствующей функцией.

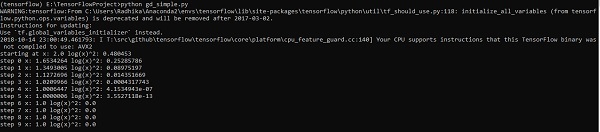
init = tf.initialize_all_variables()

def optimize():
   with tf.Session() as session:
      session.run(init)
      print("starting at", "x:", session.run(x), "log(x)^2:", session.run(log_x_squared))
      
      for step in range(10):
         session.run(train)
         print("step", step, "x:", session.run(x), "log(x)^2:", session.run(log_x_squared))
optimize()

Выше строка кода генерирует вывод, как показано на скриншоте ниже —

Мы видим, что необходимые эпохи и итерации рассчитываются, как показано в выходных данных.

TensorFlow — Формирование графиков

Дифференциальное уравнение в частных производных (PDE) — это дифференциальное уравнение, которое включает в себя частные производные с неизвестной функцией нескольких независимых переменных. Что касается дифференциальных уравнений в частных производных, мы сосредоточимся на создании новых графиков.

Предположим, есть пруд размером 500 * 500 кв.

N = 500

Теперь мы вычислим уравнение в частных производных и сформируем соответствующий граф, используя его. Рассмотрим шаги, приведенные ниже для вычисления графа.

Шаг 1 — Импорт библиотек для симуляции.

import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt

Шаг 2 — Включите функции для преобразования двумерного массива в ядро свертки и упрощенную операцию свертки 2D.

def make_kernel(a):
   a = np.asarray(a)
   a = a.reshape(list(a.shape) + [1,1])
   return tf.constant(a, dtype=1)

def simple_conv(x, k):
   """A simplified 2D convolution operation"""
   x = tf.expand_dims(tf.expand_dims(x, 0), -1)
   y = tf.nn.depthwise_conv2d(x, k, [1, 1, 1, 1], padding = 'SAME')
   return y[0, :, :, 0]

def laplace(x):
   """Compute the 2D laplacian of an array"""
   laplace_k = make_kernel([[0.5, 1.0, 0.5], [1.0, -6., 1.0], [0.5, 1.0, 0.5]])
   return simple_conv(x, laplace_k)
   
sess = tf.InteractiveSession()

Шаг 3 — Включите количество итераций и вычислите график для отображения записей соответственно.

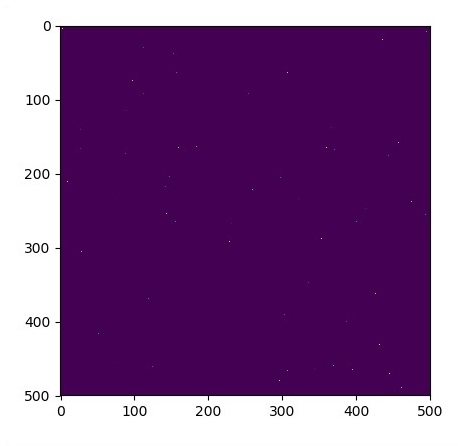
N = 500

# Initial Conditions -- some rain drops hit a pond

# Set everything to zero
u_init = np.zeros([N, N], dtype = np.float32)
ut_init = np.zeros([N, N], dtype = np.float32)

# Some rain drops hit a pond at random points
for n in range(100):
   a,b = np.random.randint(0, N, 2)
   u_init[a,b] = np.random.uniform()

plt.imshow(u_init)
plt.show()

# Parameters:
# eps -- time resolution
# damping -- wave damping
eps = tf.placeholder(tf.float32, shape = ())
damping = tf.placeholder(tf.float32, shape = ())

# Create variables for simulation state
U = tf.Variable(u_init)
Ut = tf.Variable(ut_init)

# Discretized PDE update rules
U_ = U + eps * Ut
Ut_ = Ut + eps * (laplace(U) - damping * Ut)

# Operation to update the state
step = tf.group(U.assign(U_), Ut.assign(Ut_))

# Initialize state to initial conditions
tf.initialize_all_variables().run()

# Run 1000 steps of PDE
for i in range(1000):
   # Step simulation
   step.run({eps: 0.03, damping: 0.04})
   
   # Visualize every 50 steps
   if i % 500 == 0:
      plt.imshow(U.eval())
      plt.show()

Графики построены, как показано ниже —

Распознавание изображений с использованием TensorFlow

TensorFlow включает в себя специальную функцию распознавания изображений, и эти изображения хранятся в определенной папке. С относительно одинаковыми изображениями будет легко реализовать эту логику в целях безопасности.

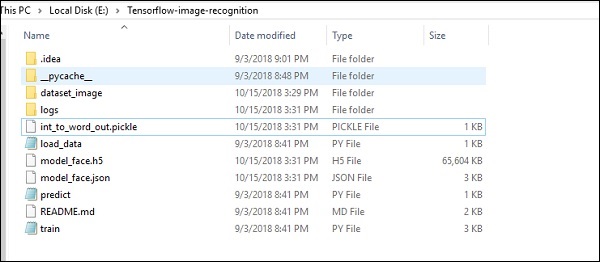
Структура папок реализации кода распознавания изображений показана ниже:

Dataset_image включает в себя связанные изображения, которые необходимо загрузить. Мы сосредоточимся на распознавании изображений с нашим логотипом, определенным в нем. Изображения загружаются с помощью скрипта «load_data.py», который помогает вести заметки о различных модулях распознавания изображений внутри них.

import pickle
from sklearn.model_selection import train_test_split
from scipy import misc

import numpy as np
import os

label = os.listdir("dataset_image")
label = label[1:]
dataset = []

for image_label in label:
   images = os.listdir("dataset_image/"+image_label)
   
   for image in images:
      img = misc.imread("dataset_image/"+image_label+"/"+image)
      img = misc.imresize(img, (64, 64))
      dataset.append((img,image_label))
X = []
Y = []

for input,image_label in dataset:
   X.append(input)
   Y.append(label.index(image_label))

X = np.array(X)
Y = np.array(Y)

X_train,y_train, = X,Y

data_set = (X_train,y_train)

save_label = open("int_to_word_out.pickle","wb")
pickle.dump(label, save_label)
save_label.close()

Обучение изображений помогает хранить распознаваемые шаблоны в указанной папке.

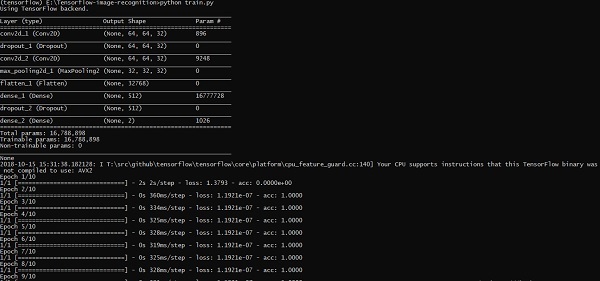
import numpy
import matplotlib.pyplot as plt

from keras.layers import Dropout
from keras.layers import Flatten
from keras.constraints import maxnorm
from keras.optimizers import SGD
from keras.layers import Conv2D
from keras.layers.convolutional import MaxPooling2D
from keras.utils import np_utils
from keras import backend as K

import load_data
from keras.models import Sequential
from keras.layers import Dense

import keras
K.set_image_dim_ordering('tf')

# fix random seed for reproducibility
seed = 7
numpy.random.seed(seed)

# load data
(X_train,y_train) = load_data.data_set

# normalize inputs from 0-255 to 0.0-1.0
X_train = X_train.astype('float32')

#X_test = X_test.astype('float32')
X_train = X_train / 255.0

#X_test = X_test / 255.0
# one hot encode outputs
y_train = np_utils.to_categorical(y_train)

#y_test = np_utils.to_categorical(y_test)
num_classes = y_train.shape[1]

# Create the model
model = Sequential()
model.add(Conv2D(32, (3, 3), input_shape = (64, 64, 3), padding = 'same', 
   activation = 'relu', kernel_constraint = maxnorm(3)))

model.add(Dropout(0.2))
model.add(Conv2D(32, (3, 3), activation = 'relu', padding = 'same', 
   kernel_constraint = maxnorm(3)))

model.add(MaxPooling2D(pool_size = (2, 2)))
model.add(Flatten())
model.add(Dense(512, activation = 'relu', kernel_constraint = maxnorm(3)))
model.add(Dropout(0.5))
model.add(Dense(num_classes, activation = 'softmax'))

# Compile model
epochs = 10
lrate = 0.01
decay = lrate/epochs
sgd = SGD(lr = lrate, momentum = 0.9, decay = decay, nesterov = False)
model.compile(loss = 'categorical_crossentropy', optimizer = sgd, metrics = ['accuracy'])
print(model.summary())

#callbacks = [keras.callbacks.EarlyStopping(
   monitor = 'val_loss', min_delta = 0, patience = 0, verbose = 0, mode = 'auto')]
callbacks = [keras.callbacks.TensorBoard(log_dir='./logs', 
   histogram_freq = 0, batch_size = 32, write_graph = True, write_grads = False, 
   write_images = True, embeddings_freq = 0, embeddings_layer_names = None, 
   embeddings_metadata = None)]

# Fit the model

model.fit(X_train, y_train, epochs = epochs, 
   batch_size = 32,shuffle = True,callbacks = callbacks)

# Final evaluation of the model
scores = model.evaluate(X_train, y_train, verbose = 0)
print("Accuracy: %.2f%%" % (scores[1]*100))

# serialize model to JSONx
model_json = model.to_json()
with open("model_face.json", "w") as json_file:
   json_file.write(model_json)

# serialize weights to HDF5
model.save_weights("model_face.h5")
print("Saved model to disk")

Выше строка кода генерирует вывод, как показано ниже —

TensorFlow — Краткое руководство

TensorFlow — Введение

Почему TensorFlow так популярен?

TensorFlow — Установка

Понимание искусственного интеллекта

Контролируемое обучение

Обучение без учителя

TensorFlow — математические основы

Вектор

скаляр

матрица

Математические вычисления

Добавление матриц

Вычитание матриц

Умножение матриц

Транспонировать матрицы

Точечное произведение векторов

Машинное обучение и глубокое обучение

Машинное обучение

Глубокое обучение

Разница между машинным обучением и глубоким обучением

Количество данных

Аппаратные зависимости

Характеристика

Подход к решению проблем

Время исполнения

Интерпретируемость

Применение машинного обучения и глубокого обучения

Будущие тенденции

Заключение

TensorFlow — Основы

Тензорная структура данных

Ранг

форма

Тип

Различные размеры TensorFlow

Одномерный тензор

Двумерные тензоры

Тензорная обработка и манипуляции

объяснение

TensorFlow — сверточные нейронные сети

Сверточные нейронные сети

Внедрение TensorFlow CNN

TensorFlow — Рекуррентные нейронные сети

Рекуррентная реализация нейронной сети с TensorFlow

TensorFlow — Визуализация TensorBoard

TensorFlow — вложение слов

Word2vec

Выход

TensorFlow — однослойный персептрон

Однослойный персептрон

Выход

TensorFlow — Линейная регрессия

Шаги по разработке алгоритма линейной регрессии

Шаг 1

Шаг 2

Шаг 3

Шаг 4

TensorFlow — TFLearn и его установка

TensorFlow — разница CNN и RNN

Тензорфлоу — Керас

TensorFlow — распределенные вычисления

TensorFlow — Экспорт

TensorFlow — многослойное обучение персептрону

TensorFlow — скрытые слои персептрона

Выход

TensorFlow — оптимизаторы

TensorFlow — реализация XOR

TensorFlow — Оптимизация градиентного спуска

Шаг 1

Шаг 2

TensorFlow — Формирование графиков

Распознавание изображений с использованием TensorFlow

Рекомендации по обучению нейронной сети

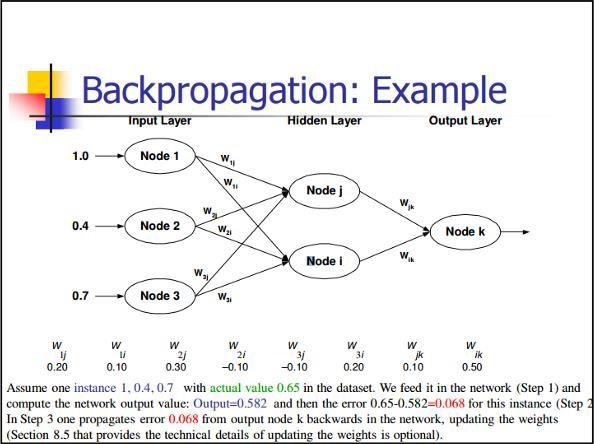
Обратное распространение

Стохастический градиентный спуск

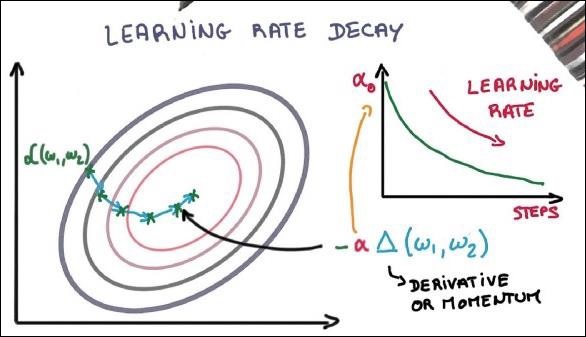
Скорость обучения

Выбывать

Макс Пул

Долгосрочная кратковременная память (LSTM)