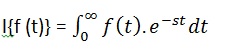MATLAB — Преобразования

MATLAB предоставляет команду для работы с преобразованиями, такими как преобразования Лапласа и Фурье. Преобразования используются в науке и технике как инструмент для упрощения анализа и анализа данных с другой стороны.

Например, преобразование Фурье позволяет нам преобразовывать сигнал, представленный как функцию времени, в функцию частоты. Преобразование Лапласа позволяет преобразовать дифференциальное уравнение в алгебраическое уравнение.

MATLAB предоставляет команды laplace , fourier и fft для работы с преобразованиями Laplace, Fourier и Fast Fourier.

Преобразование Лапласа

Преобразование Лапласа функции времени f (t) задается следующим интегралом:

Преобразование Лапласа также обозначается как преобразование f (t) в F (s). Вы можете видеть, что этот процесс преобразования или интеграции преобразует функцию f (t) символической переменной t в другую функцию F (s) с другой переменной s.

Преобразование Лапласа превращает дифференциальные уравнения в алгебраические. Чтобы вычислить преобразование Лапласа функции f (t), напишите —

laplace(f(t))

пример

В этом примере мы вычислим преобразование Лапласа некоторых часто используемых функций.

Создайте файл сценария и введите следующий код —

syms s t a b w

laplace(a)
laplace(t^2)
laplace(t^9)
laplace(exp(-b*t))
laplace(sin(w*t))
laplace(cos(w*t))

Когда вы запускаете файл, он показывает следующий результат —

ans =
   1/s^2

ans =
   2/s^3

ans =
   362880/s^10

ans =
   1/(b + s)
  
ans =
   w/(s^2 + w^2)
  
ans =
   s/(s^2 + w^2)

Обратное преобразование Лапласа

MATLAB позволяет нам вычислять обратное преобразование Лапласа, используя команду ilaplace .

Например,

ilaplace(1/s^3)

MATLAB выполнит приведенную выше инструкцию и отобразит результат —

ans =
   t^2/2

пример

Создайте файл сценария и введите следующий код —

syms s t a b w

ilaplace(1/s^7)
ilaplace(2/(w+s))
ilaplace(s/(s^2+4))
ilaplace(exp(-b*t))
ilaplace(w/(s^2 + w^2))
ilaplace(s/(s^2 + w^2))

Когда вы запускаете файл, он показывает следующий результат —

ans =
   t^6/720

ans =
   2*exp(-t*w)

ans =
   cos(2*t)

ans =
   ilaplace(exp(-b*t), t, x)

ans =
   sin(t*w)

ans =
   cos(t*w)

Преобразования Фурье

Преобразования Фурье обычно преобразуют математическую функцию времени f (t) в новую функцию, иногда обозначаемую или F, аргумент которой — частота с единицами циклов / с (герц) или радианами в секунду. Новая функция тогда называется преобразованием Фурье и / или частотным спектром функции f.

пример

Создайте файл сценария и введите в нем следующий код —

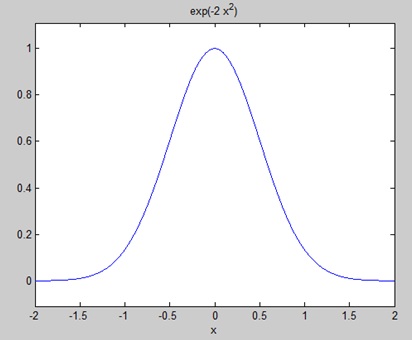
syms x 
f = exp(-2*x^2);     %our function
ezplot(f,[-2,2])     % plot of our function
FT = fourier(f)      % Fourier transform

Когда вы запускаете файл, MATLAB строит следующий график —

Следующий результат отображается —

FT =
   (2^(1/2)*pi^(1/2)*exp(-w^2/8))/2

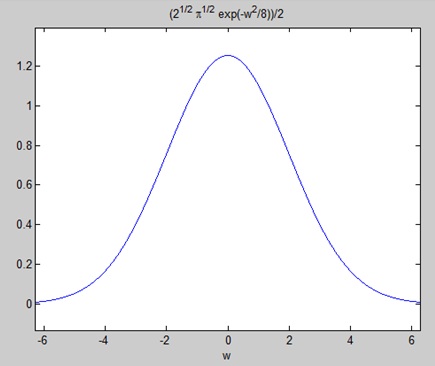
Построение преобразования Фурье как —

ezplot(FT)

Дает следующий график —

Обратные преобразования Фурье

MATLAB предоставляет команду ifourier для вычисления обратного преобразования Фурье функции. Например,

f = ifourier(-2*exp(-abs(w)))

MATLAB выполнит приведенную выше инструкцию и отобразит результат —