MATLAB предоставляет команду diff для вычисления символьных производных. В простейшей форме вы передаете функцию, которую вы хотите дифференцировать, команде diff в качестве аргумента.
Например, давайте вычислим производную функции f (t) = 3t 2 + 2t -2
пример
Создайте файл сценария и введите в него следующий код —
syms t f = 3*t^2 + 2*t^(-2); diff(f)
Когда приведенный выше код компилируется и выполняется, он дает следующий результат —
ans = 6*t - 4/t^3
Ниже приведен октавный эквивалент приведенного выше расчета —
pkg load symbolic symbols t = sym("t"); f = 3*t^2 + 2*t^(-2); differentiate(f,t)
Octave выполняет код и возвращает следующий результат —
ans = -(4.0)*t^(-3.0)+(6.0)*t
Проверка элементарных правил дифференциации
Кратко сформулируем различные уравнения или правила дифференцирования функций и проверим эти правила. Для этого мы напишем f ‘(x) для производной первого порядка и f «(x) для производной второго порядка.
Ниже приведены правила для дифференциации —
Правило 1
Для любых функций f и g и любых действительных чисел a и b являются производными функции —
h (x) = af (x) + bg (x) относительно x определяется как —
h ‘(x) = af’ (x) + bg ‘(x)
Правило 2
Правила сумм и вычитаний гласят, что если f и g две функции, то f ‘и g’ являются их производными соответственно, тогда
( f + g) ‘= f’ + g ‘
(f — g) ‘= f’ — g ‘
Правило 3
Правило произведения гласит, что если f и g две функции, f ‘и g’ являются их производными соответственно, то
(fg) ‘= f’.g + g’.f
Правило 4
Правило отношения гласит, что если f и g две функции, f ‘и g’ являются их производными соответственно, то
(f / g) ‘= (f’.g — g’.f) / g 2
Правило 5
Полиномиальное или элементарное степенное правило гласит, что если y = f (x) = x n , то f ‘= n. х (н-1)
Прямым результатом этого правила является то, что производная любой константы равна нулю, т. Е. Если y = k , любая константа, то
f ‘= 0
Правило 6
Правило цепочки гласит, что производная функции функции h (x) = f (g (x)) по x равна
h ‘(x) = f’ (g (x)). g ‘(x)
пример
Создайте файл сценария и введите в него следующий код —
syms x syms t f = (x + 2)*(x^2 + 3) der1 = diff(f) f = (t^2 + 3)*(sqrt(t) + t^3) der2 = diff(f) f = (x^2 - 2*x + 1)*(3*x^3 - 5*x^2 + 2) der3 = diff(f) f = (2*x^2 + 3*x)/(x^3 + 1) der4 = diff(f) f = (x^2 + 1)^17 der5 = diff(f) f = (t^3 + 3* t^2 + 5*t -9)^(-6) der6 = diff(f)
Когда вы запускаете файл, MATLAB отображает следующий результат —
f = (x^2 + 3)*(x + 2) der1 = 2*x*(x + 2) + x^2 + 3 f = (t^(1/2) + t^3)*(t^2 + 3) der2 = (t^2 + 3)*(3*t^2 + 1/(2*t^(1/2))) + 2*t*(t^(1/2) + t^3) f = (x^2 - 2*x + 1)*(3*x^3 - 5*x^2 + 2) der3 = (2*x - 2)*(3*x^3 - 5*x^2 + 2) - (- 9*x^2 + 10*x)*(x^2 - 2*x + 1) f = (2*x^2 + 3*x)/(x^3 + 1) der4 = (4*x + 3)/(x^3 + 1) - (3*x^2*(2*x^2 + 3*x))/(x^3 + 1)^2 f = (x^2 + 1)^17 der5 = 34*x*(x^2 + 1)^16 f = 1/(t^3 + 3*t^2 + 5*t - 9)^6 der6 = -(6*(3*t^2 + 6*t + 5))/(t^3 + 3*t^2 + 5*t - 9)^7
Ниже приведен октавный эквивалент приведенного выше расчета —
pkg load symbolic symbols x = sym("x"); t = sym("t"); f = (x + 2)*(x^2 + 3) der1 = differentiate(f,x) f = (t^2 + 3)*(t^(1/2) + t^3) der2 = differentiate(f,t) f = (x^2 - 2*x + 1)*(3*x^3 - 5*x^2 + 2) der3 = differentiate(f,x) f = (2*x^2 + 3*x)/(x^3 + 1) der4 = differentiate(f,x) f = (x^2 + 1)^17 der5 = differentiate(f,x) f = (t^3 + 3* t^2 + 5*t -9)^(-6) der6 = differentiate(f,t)
Octave выполняет код и возвращает следующий результат —
f = (2.0+x)*(3.0+x^(2.0)) der1 = 3.0+x^(2.0)+(2.0)*(2.0+x)*x f = (t^(3.0)+sqrt(t))*(3.0+t^(2.0)) der2 = (2.0)*(t^(3.0)+sqrt(t))*t+((3.0)*t^(2.0)+(0.5)*t^(-0.5))*(3.0+t^(2.0)) f = (1.0+x^(2.0)-(2.0)*x)*(2.0-(5.0)*x^(2.0)+(3.0)*x^(3.0)) der3 = (-2.0+(2.0)*x)*(2.0-(5.0)*x^(2.0)+(3.0)*x^(3.0))+((9.0)*x^(2.0)-(10.0)*x)*(1.0+x^(2.0)-(2.0)*x) f = (1.0+x^(3.0))^(-1)*((2.0)*x^(2.0)+(3.0)*x) der4 = (1.0+x^(3.0))^(-1)*(3.0+(4.0)*x)-(3.0)*(1.0+x^(3.0))^(-2)*x^(2.0)*((2.0)*x^(2.0)+(3.0)*x) f = (1.0+x^(2.0))^(17.0) der5 = (34.0)*(1.0+x^(2.0))^(16.0)*x f = (-9.0+(3.0)*t^(2.0)+t^(3.0)+(5.0)*t)^(-6.0) der6 = -(6.0)*(-9.0+(3.0)*t^(2.0)+t^(3.0)+(5.0)*t)^(-7.0)*(5.0+(3.0)*t^(2.0)+(6.0)*t)
Производные экспоненциальных, логарифмических и тригонометрических функций
В следующей таблице приведены производные от часто используемых экспоненциальных, логарифмических и тригонометрических функций.
| функция | производный |
|---|---|
| топор с | c ax. ln ca (ln — натуральный логарифм) |
| е х | е х |
| ln x | 1 / х |
| ln c x | 1 / x.ln c |
| х х | х х (1 + лн х) |
| грех (х) | сов (х) |
| сов (х) | -sin (х) |
| тангенс (х) | sec 2 (x), или 1 / cos 2 (x), или 1 + tan 2 (x) |
| кроватка (х) | -csc 2 (x) или -1 / sin 2 (x) или — (1 + кроватка 2 (x)) |
| с (х) | с (х) .tan (х) |
| CSC (х) | -csc (х) .cot (х) |
пример
Создайте файл сценария и введите в него следующий код —
syms x y = exp(x) diff(y) y = x^9 diff(y) y = sin(x) diff(y) y = tan(x) diff(y) y = cos(x) diff(y) y = log(x) diff(y) y = log10(x) diff(y) y = sin(x)^2 diff(y) y = cos(3*x^2 + 2*x + 1) diff(y) y = exp(x)/sin(x) diff(y)
Когда вы запускаете файл, MATLAB отображает следующий результат —
y = exp(x) ans = exp(x) y = x^9 ans = 9*x^8 y = sin(x) ans = cos(x) y = tan(x) ans = tan(x)^2 + 1 y = cos(x) ans = -sin(x) y = log(x) ans = 1/x y = log(x)/log(10) ans = 1/(x*log(10)) y = sin(x)^2 ans = 2*cos(x)*sin(x) y = cos(3*x^2 + 2*x + 1) ans = -sin(3*x^2 + 2*x + 1)*(6*x + 2) y = exp(x)/sin(x) ans = exp(x)/sin(x) - (exp(x)*cos(x))/sin(x)^2
Ниже приведен октавный эквивалент приведенного выше расчета —
pkg load symbolic symbols x = sym("x"); y = Exp(x) differentiate(y,x) y = x^9 differentiate(y,x) y = Sin(x) differentiate(y,x) y = Tan(x) differentiate(y,x) y = Cos(x) differentiate(y,x) y = Log(x) differentiate(y,x) % symbolic packages does not have this support %y = Log10(x) %differentiate(y,x) y = Sin(x)^2 differentiate(y,x) y = Cos(3*x^2 + 2*x + 1) differentiate(y,x) y = Exp(x)/Sin(x) differentiate(y,x)
Octave выполняет код и возвращает следующий результат —
y = exp(x) ans = exp(x) y = x^(9.0) ans = (9.0)*x^(8.0) y = sin(x) ans = cos(x) y = tan(x) ans = 1+tan(x)^2 y = cos(x) ans = -sin(x) y = log(x) ans = x^(-1) y = sin(x)^(2.0) ans = (2.0)*sin(x)*cos(x) y = cos(1.0+(2.0)*x+(3.0)*x^(2.0)) ans = -(2.0+(6.0)*x)*sin(1.0+(2.0)*x+(3.0)*x^(2.0)) y = sin(x)^(-1)*exp(x) ans = sin(x)^(-1)*exp(x)-sin(x)^(-2)*cos(x)*exp(x)
Вычисление производных высшего порядка
Для вычисления старших производных функции f мы используем синтаксис diff (f, n) .
Вычислим вторую производную функции y = f (x) = x .e -3x
f = x*exp(-3*x); diff(f, 2)
MATLAB выполняет код и возвращает следующий результат —
ans = 9*x*exp(-3*x) - 6*exp(-3*x)
Ниже приведен октавный эквивалент приведенного выше расчета —
pkg load symbolic symbols x = sym("x"); f = x*Exp(-3*x); differentiate(f, x, 2)
Octave выполняет код и возвращает следующий результат —
ans = (9.0)*exp(-(3.0)*x)*x-(6.0)*exp(-(3.0)*x)
пример
В этом примере давайте решим проблему. Учитывая, что функция y = f (x) = 3 sin (x) + 7 cos (5x) . Нам нужно выяснить, выполняется ли уравнение f «+ f = -5cos (2x) .
Создайте файл сценария и введите в него следующий код —
syms x y = 3*sin(x)+7*cos(5*x); % defining the function lhs = diff(y,2)+y; %evaluting the lhs of the equation rhs = -5*cos(2*x); %rhs of the equation if(isequal(lhs,rhs)) disp('Yes, the equation holds true'); else disp('No, the equation does not hold true'); end disp('Value of LHS is: '), disp(lhs);
Когда вы запускаете файл, он показывает следующий результат —
No, the equation does not hold true Value of LHS is: -168*cos(5*x)
Ниже приведен октавный эквивалент приведенного выше расчета —
pkg load symbolic symbols x = sym("x"); y = 3*Sin(x)+7*Cos(5*x); % defining the function lhs = differentiate(y, x, 2) + y; %evaluting the lhs of the equation rhs = -5*Cos(2*x); %rhs of the equation if(lhs == rhs) disp('Yes, the equation holds true'); else disp('No, the equation does not hold true'); end disp('Value of LHS is: '), disp(lhs);
Octave выполняет код и возвращает следующий результат —
No, the equation does not hold true Value of LHS is: -(168.0)*cos((5.0)*x)
Нахождение максимумов и минимумов кривой
Если мы ищем локальные максимумы и минимумы для графика, мы в основном ищем самые высокие или самые низкие точки на графике функции в определенной местности или для определенного диапазона значений символической переменной.
Для функции y = f (x) точки на графе, где граф имеет нулевой наклон, называются стационарными точками . Другими словами, стационарные точки — это где f ‘(x) = 0.
Чтобы найти стационарные точки функции, которую мы дифференцируем, нам нужно установить производную равной нулю и решить уравнение.
пример
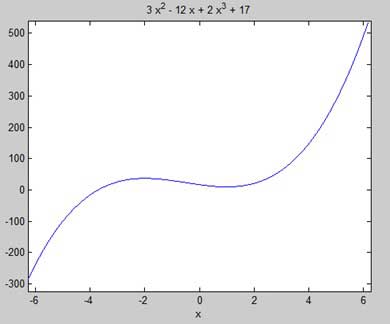
Найдем стационарные точки функции f (x) = 2x 3 + 3x 2 — 12x + 17
Сделайте следующие шаги —
Сначала давайте введем функцию и построим ее график.
syms x y = 2*x^3 + 3*x^2 - 12*x + 17; % defining the function ezplot(y)
MATLAB выполняет код и возвращает следующий график —
Вот октавный эквивалентный код для приведенного выше примера —
pkg load symbolic symbols x = sym('x'); y = inline("2*x^3 + 3*x^2 - 12*x + 17"); ezplot(y) print -deps graph.eps
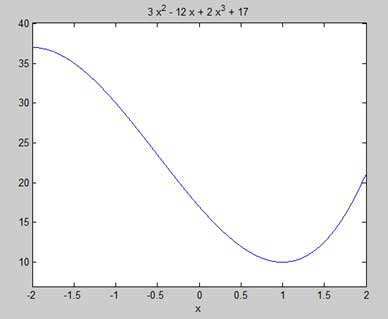
Наша цель — найти некоторые локальные максимумы и минимумы на графике, поэтому давайте найдем локальные максимумы и минимумы для интервала [-2, 2] на графике.
syms x y = 2*x^3 + 3*x^2 - 12*x + 17; % defining the function ezplot(y, [-2, 2])
MATLAB выполняет код и возвращает следующий график —
Вот октавный эквивалентный код для приведенного выше примера —
pkg load symbolic symbols x = sym('x'); y = inline("2*x^3 + 3*x^2 - 12*x + 17"); ezplot(y, [-2, 2]) print -deps graph.eps
Далее, давайте вычислим производную.
g = diff(y)
MATLAB выполняет код и возвращает следующий результат —
g = 6*x^2 + 6*x - 12
Вот октавный эквивалент приведенного выше расчета —
pkg load symbolic symbols x = sym("x"); y = 2*x^3 + 3*x^2 - 12*x + 17; g = differentiate(y,x)
Octave выполняет код и возвращает следующий результат —
g = -12.0+(6.0)*x+(6.0)*x^(2.0)
Давайте решим производную функцию g, чтобы получить значения, где она становится равной нулю.
s = solve(g)
MATLAB выполняет код и возвращает следующий результат —
s = 1 -2
Ниже приведен октавный эквивалент приведенного выше расчета —
pkg load symbolic symbols x = sym("x"); y = 2*x^3 + 3*x^2 - 12*x + 17; g = differentiate(y,x) roots([6, 6, -12])
Octave выполняет код и возвращает следующий результат —
g = -12.0+(6.0)*x^(2.0)+(6.0)*x ans = -2 1
Это согласуется с нашим сюжетом. Итак, давайте оценим функцию f в критических точках x = 1, -2. Мы можем подставить значение в символическую функцию с помощью команды subs .
subs(y, 1), subs(y, -2)
MATLAB выполняет код и возвращает следующий результат —
ans = 10 ans = 37
Ниже приведен октавный эквивалент приведенного выше расчета —
pkg load symbolic symbols x = sym("x"); y = 2*x^3 + 3*x^2 - 12*x + 17; g = differentiate(y,x) roots([6, 6, -12]) subs(y, x, 1), subs(y, x, -2)
ans = 10.0 ans = 37.0-4.6734207789940138748E-18*I
Следовательно, минимальное и максимальное значения для функции f (x) = 2x 3 + 3x 2 — 12x + 17 в интервале [-2,2] составляют 10 и 37.
Решение дифференциальных уравнений
MATLAB предоставляет команду dsolve для символического решения дифференциальных уравнений.
Наиболее простой формой команды dsolve для поиска решения одного уравнения является
dsolve('eqn')
где eqn — текстовая строка, используемая для ввода уравнения.
Он возвращает символическое решение с набором произвольных констант, которые MATLAB помечает C1, C2 и так далее.
Вы также можете указать начальные и граничные условия для задачи в виде списка с разделителями-запятыми после уравнения в виде —
dsolve('eqn','cond1', 'cond2',…)
В целях использования команды dsolve производные обозначены знаком D. Например, уравнение типа f ‘(t) = -2 * f + стоимость (t) вводится как —
‘Df = -2 * f + cos (t)’
Высшие производные обозначены следующим за D порядком производной.
Например, уравнение f «(x) + 2f ‘(x) = 5sin3x должно быть введено как —
‘D2y + 2Dy = 5 * sin (3 * x)’
Давайте рассмотрим простой пример дифференциального уравнения первого порядка: y ‘= 5y.
s = dsolve('Dy = 5*y')
MATLAB выполняет код и возвращает следующий результат —
s = C2*exp(5*t)
Давайте рассмотрим другой пример дифференциального уравнения второго порядка: y «- y = 0, y (0) = -1, y ‘(0) = 2.
dsolve('D2y - y = 0','y(0) = -1','Dy(0) = 2')
MATLAB выполняет код и возвращает следующий результат —