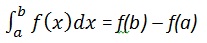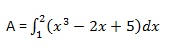Учебники

MATLAB — Интеграция

Ноябрь 13, 2018

Интеграция имеет дело с двумя принципиально разными типами проблем.

  • В первом типе дается производная функции, и мы хотим найти функцию. Поэтому мы в основном обращаем вспять процесс дифференциации. Этот обратный процесс известен как антидифференцирование, или нахождение примитивной функции, или нахождение неопределенного интеграла .

  • Второй тип проблем включает сложение очень большого количества очень маленьких величин, а затем определение предела, когда размер величин приближается к нулю, а число членов стремится к бесконечности. Этот процесс приводит к определению определенного интеграла .

В первом типе дается производная функции, и мы хотим найти функцию. Поэтому мы в основном обращаем вспять процесс дифференциации. Этот обратный процесс известен как антидифференцирование, или нахождение примитивной функции, или нахождение неопределенного интеграла .

Второй тип проблем включает сложение очень большого количества очень маленьких величин, а затем определение предела, когда размер величин приближается к нулю, а число членов стремится к бесконечности. Этот процесс приводит к определению определенного интеграла .

Определенные интегралы используются для определения площади, объема, центра тяжести, момента инерции, работы, выполняемой силой, и во многих других приложениях.

Поиск неопределенного интеграла с помощью MATLAB

По определению, если производная функции f (x) есть f ‘(x), то мы говорим, что неопределенный интеграл от f’ (x) по x равен f (x). Например, поскольку производная (по x) x 2 равна 2x, мы можем сказать, что неопределенный интеграл от 2x равен x 2 .

В символах —

f ‘(x 2 ) = 2x , следовательно,

∫ 2xdx = x 2 .

Неопределенный интеграл не является уникальным, потому что производная x 2 + c для любого значения константы c также будет 2x.

Это выражается в символах как —

∫ 2xdx = x 2 + c .

Где c называется «произвольной константой».

MATLAB предоставляет команду int для вычисления интеграла выражения. Чтобы вывести выражение для неопределенного интеграла функции, мы пишем — 

int(f);

Например, из нашего предыдущего примера — 

syms x 
int(2*x)

MATLAB выполняет приведенный выше оператор и возвращает следующий результат — 

ans =
   x^2

Пример 1

В этом примере давайте найдем интеграл некоторых часто используемых выражений. Создайте файл сценария и введите в нем следующий код — 

syms x n

int(sym(x^n))
f = 'sin(n*t)'
int(sym(f))
syms a t
int(a*cos(pi*t))
int(a^x)

Когда вы запускаете файл, он показывает следующий результат — 

ans =
   piecewise([n == -1, log(x)], [n ~= -1, x^(n + 1)/(n + 1)])
f =
sin(n*t)
ans =
   -cos(n*t)/n
   ans =
   (a*sin(pi*t))/pi
   ans =
   a^x/log(a)

Пример 2

Создайте файл сценария и введите в нем следующий код — 

syms x n
int(cos(x))
int(exp(x))
int(log(x))
int(x^-1)
int(x^5*cos(5*x))
pretty(int(x^5*cos(5*x)))

int(x^-5)
int(sec(x)^2)
pretty(int(1 - 10*x + 9 * x^2))

int((3 + 5*x -6*x^2 - 7*x^3)/2*x^2)
pretty(int((3 + 5*x -6*x^2 - 7*x^3)/2*x^2))

Обратите внимание, что функция pretty возвращает выражение в более читаемом формате.

Когда вы запускаете файл, он показывает следующий результат — 

ans =
   sin(x)
 
ans =
   exp(x)
 
ans =
   x*(log(x) - 1)
 
ans =
   log(x)
 
ans =
(24*cos(5*x))/3125 + (24*x*sin(5*x))/625 - (12*x^2*cos(5*x))/125 + (x^4*cos(5*x))/5 - (4*x^3*sin(5*x))/25 + (x^5*sin(5*x))/5
                                    2             4 
   24 cos(5 x)   24 x sin(5 x)   12 x  cos(5 x)   x  cos(5 x) 
   ----------- + ------------- - -------------- + ------------ 
      3125            625             125              5 
   
        3             5 
 
   4 x  sin(5 x)   x  sin(5 x) 
   ------------- + ----------- 
         25              5
 
ans =
-1/(4*x^4)
 
ans =
tan(x)
        2 
  x (3 x  - 5 x + 1)
 
ans = 
- (7*x^6)/12 - (3*x^5)/5 + (5*x^4)/8 + x^3/2
 
      6      5      4    3 
    7 x    3 x    5 x    x 
  - ---- - ---- + ---- + -- 
     12     5      8     2

Нахождение определенного интеграла с помощью MATLAB

По определению, определенный интеграл в основном является пределом суммы. Мы используем определенные интегралы, чтобы найти области, такие как область между кривой и осью x и область между двумя кривыми. Определенные интегралы могут также использоваться в других ситуациях, где требуемое количество может быть выражено как предел суммы.

Функция int может использоваться для определенной интеграции, передавая пределы, по которым вы хотите вычислить интеграл.

Вычислять

Определенный Интеграл

мы пишем, 

int(x, a, b)

Например, для расчета стоимости 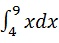пример мы пишем — 

int(x, 4, 9)

MATLAB выполняет приведенный выше оператор и возвращает следующий результат — 

ans =
   65/2

Ниже приведен октавный эквивалент приведенного выше расчета — 

pkg load symbolic
symbols

x = sym("x");
f = x;
c = [1, 0];
integral = polyint(c);

a = polyval(integral, 9) - polyval(integral, 4);
display('Area: '), disp(double(a));

Octave выполняет код и возвращает следующий результат — 

Area: 

   32.500

Альтернативное решение может быть дано с помощью функции quad (), предоставляемой Octave следующим образом: 

pkg load symbolic
symbols

f = inline("x");
[a, ierror, nfneval] = quad(f, 4, 9);

display('Area: '), disp(double(a));

Octave выполняет код и возвращает следующий результат — 

Area: 
   32.500

Пример 1

Вычислим площадь, заключенную между осью x и кривой y = x 3 -2x + 5 и ординатами x = 1 и x = 2.

Требуемая площадь определяется как —

Расчет площади

Создайте файл сценария и введите следующий код — 

f = x^3 - 2*x +5;
a = int(f, 1, 2)
display('Area: '), disp(double(a));

Когда вы запускаете файл, он показывает следующий результат — 

a =
23/4
Area: 
   5.7500

Ниже приведен октавный эквивалент приведенного выше расчета — 

pkg load symbolic
symbols

x = sym("x");
f = x^3 - 2*x +5;
c = [1, 0, -2, 5];
integral = polyint(c);

a = polyval(integral, 2) - polyval(integral, 1);
display('Area: '), disp(double(a));

Octave выполняет код и возвращает следующий результат — 

Area: 

   5.7500

Альтернативное решение может быть дано с помощью функции quad (), предоставляемой Octave следующим образом: 

pkg load symbolic
symbols

x = sym("x");
f = inline("x^3 - 2*x +5");

[a, ierror, nfneval] = quad(f, 1, 2);
display('Area: '), disp(double(a));

Octave выполняет код и возвращает следующий результат — 

Area: 
   5.7500

Пример 2

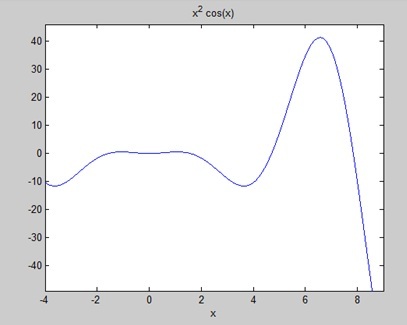
Найдите площадь под кривой: f (x) = x 2 cos (x) для −4 ≤ x ≤ 9.

Создайте файл сценария и напишите следующий код — 

f = x^2*cos(x);
ezplot(f, [-4,9])
a = int(f, -4, 9)
disp('Area: '), disp(double(a));

Когда вы запускаете файл, MATLAB строит график —

Определенный Интеграл

Выход дан ниже — 

a = 
8*cos(4) + 18*cos(9) + 14*sin(4) + 79*sin(9)
 
Area: 
   0.3326

Ниже приведен октавный эквивалент приведенного выше расчета —

291
Share: