Цифровая связь — аналого-цифровая

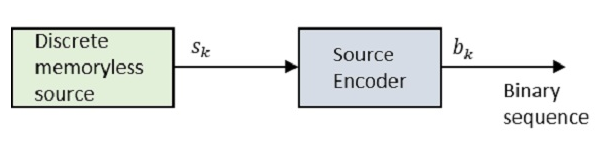
Общение, которое происходит в нашей повседневной жизни, происходит в форме сигналов. Эти сигналы, такие как звуковые сигналы, как правило, имеют аналоговый характер. Когда связь должна быть установлена ​​на расстоянии, тогда аналоговые сигналы передаются по проводам, используя различные методы для эффективной передачи.

Необходимость оцифровки

Традиционные методы связи используют аналоговые сигналы для связи на большие расстояния, которые страдают от многих потерь, таких как искажения, помехи и другие потери, включая нарушения безопасности.

Чтобы преодолеть эти проблемы, сигналы оцифровываются с использованием различных методов. Оцифрованные сигналы позволяют более четкой и точной связи без потерь.

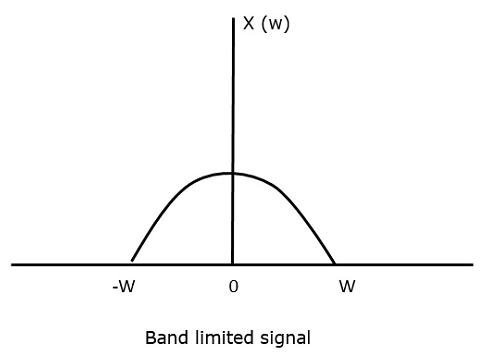
На следующем рисунке показана разница между аналоговыми и цифровыми сигналами. Цифровые сигналы состоят из 1 и 0, которые указывают высокие и низкие значения соответственно.

Преимущества цифровой связи

Поскольку сигналы оцифровываются, существует много преимуществ цифровой связи по сравнению с аналоговой связью, таких как —

• Влияние искажений, шума и помех значительно меньше в цифровых сигналах, поскольку они менее подвержены влиянию.

• Цифровые схемы более надежны.

• Цифровые схемы просты в разработке и дешевле аналоговых.

• Аппаратная реализация в цифровых схемах более гибкая, чем аналоговая.

• Появление перекрестных помех очень редко встречается в цифровой связи.

• Сигнал не изменяется, так как импульсу требуется сильное возмущение, чтобы изменить его свойства, что очень сложно.

• Функции обработки сигналов, такие как шифрование и сжатие, используются в цифровых каналах для сохранения секретности информации.

• Вероятность возникновения ошибки уменьшается за счет использования кодов обнаружения ошибок и исправления ошибок.

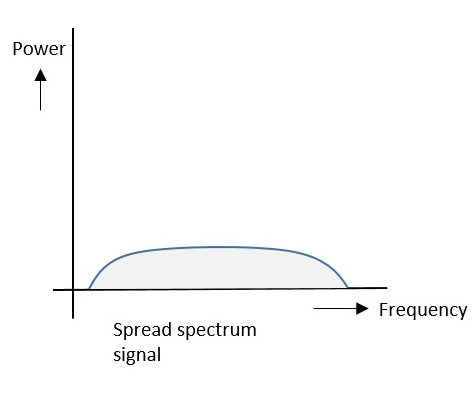
• Метод расширенного спектра используется, чтобы избежать помех.

• Объединение цифровых сигналов с использованием мультиплексирования с временным разделением (TDM) проще, чем объединение аналоговых сигналов с использованием мультиплексирования с частотным разделением (FDM).

• Процесс настройки цифровых сигналов проще, чем аналоговых сигналов.

• Цифровые сигналы могут быть сохранены и извлечены более удобно, чем аналоговые сигналы.

• Многие из цифровых схем имеют почти общие методы кодирования, и, следовательно, аналогичные устройства могут использоваться для ряда целей.

• Пропускная способность канала эффективно используется цифровыми сигналами.

Влияние искажений, шума и помех значительно меньше в цифровых сигналах, поскольку они менее подвержены влиянию.

Цифровые схемы более надежны.

Цифровые схемы просты в разработке и дешевле аналоговых.

Аппаратная реализация в цифровых схемах более гибкая, чем аналоговая.

Появление перекрестных помех очень редко встречается в цифровой связи.

Сигнал не изменяется, так как импульсу требуется сильное возмущение, чтобы изменить его свойства, что очень сложно.

Функции обработки сигналов, такие как шифрование и сжатие, используются в цифровых каналах для сохранения секретности информации.

Вероятность возникновения ошибки уменьшается за счет использования кодов обнаружения ошибок и исправления ошибок.

Метод расширенного спектра используется, чтобы избежать помех.

Объединение цифровых сигналов с использованием мультиплексирования с временным разделением (TDM) проще, чем объединение аналоговых сигналов с использованием мультиплексирования с частотным разделением (FDM).

Процесс настройки цифровых сигналов проще, чем аналоговых сигналов.

Цифровые сигналы могут быть сохранены и извлечены более удобно, чем аналоговые сигналы.

Многие из цифровых схем имеют почти общие методы кодирования, и, следовательно, аналогичные устройства могут использоваться для ряда целей.

Пропускная способность канала эффективно используется цифровыми сигналами.

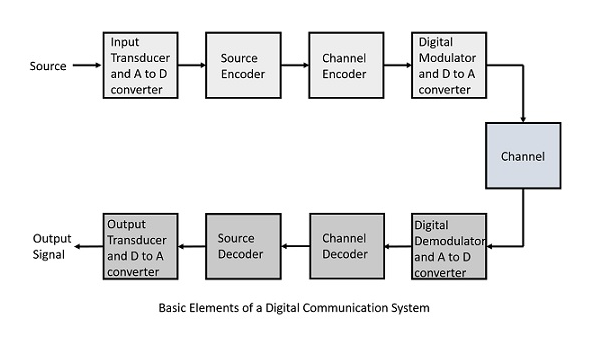
Элементы цифровой связи

Элементы, которые формируют цифровую систему связи, представлены следующей блок-схемой для простоты понимания.

Ниже приведены разделы цифровой системы связи.

Источник

Источником может быть аналоговый сигнал. Пример : звуковой сигнал

Входной преобразователь

Это преобразователь, который принимает физический вход и преобразует его в электрический сигнал (например, микрофон). Этот блок также состоит из аналого-цифрового преобразователя, где цифровой сигнал необходим для дальнейших процессов.

Цифровой сигнал обычно представлен двоичной последовательностью.

Исходный кодер

Исходный кодер сжимает данные в минимальное количество битов. Этот процесс помогает эффективно использовать пропускную способность. Он удаляет избыточные биты (ненужные лишние биты, т. Е. Нули).

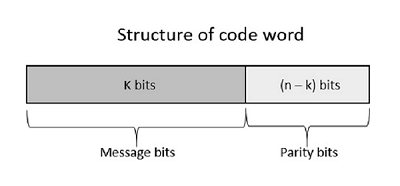
Канальный кодер

Канальный кодер, выполняет кодирование для исправления ошибок. Во время передачи сигнала из-за шума в канале сигнал может быть изменен и, следовательно, чтобы избежать этого, канальный кодер добавляет некоторые избыточные биты к передаваемым данным. Это биты, исправляющие ошибки.

Цифровой модулятор

Передаваемый сигнал здесь модулируется несущей. Сигнал также преобразуется в аналоговый из цифровой последовательности, чтобы заставить его проходить через канал или среду.

канал

Канал или среда, позволяет аналоговому сигналу передавать от конца передатчика к концу приемника.

Цифровой демодулятор

Это первый шаг на стороне получателя. Полученный сигнал демодулируется, а также снова преобразуется из аналогового в цифровой. Сигнал восстанавливается здесь.

Канальный декодер

Канальный декодер, после обнаружения последовательности, делает некоторые исправления ошибок. Искажения, которые могут возникнуть во время передачи, исправляются путем добавления некоторых избыточных битов. Это добавление битов помогает в полном восстановлении исходного сигнала.

Исходный декодер

Результирующий сигнал снова оцифровывается путем дискретизации и квантования, так что чистый цифровой выход получается без потери информации. Исходный декодер воссоздает исходный вывод.

Выходной преобразователь

Это последний блок, который преобразует сигнал в исходную физическую форму, которая была на входе передатчика. Он преобразует электрический сигнал в физический выход (например, громкоговоритель).

Выходной сигнал

Это результат, который создается после всего процесса. Пример — Звуковой сигнал получен.

Это подразделение занималось внедрением, оцифровкой сигналов, преимуществами и элементами цифровой связи. В следующих главах мы подробно узнаем о концепции цифровой связи.

Импульсная кодовая модуляция

Модуляция — это процесс изменения одного или нескольких параметров сигнала несущей в соответствии с мгновенными значениями сигнала сообщения.

Сигнал сообщения — это сигнал, который передается для связи, а сигнал несущей — это высокочастотный сигнал, который не имеет данных, но используется для передачи на большие расстояния.

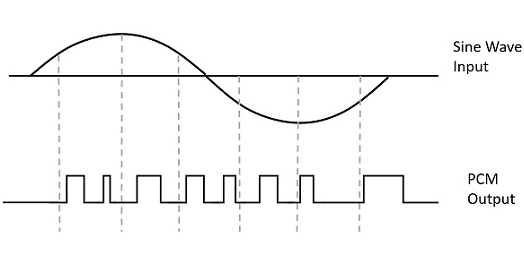
Существует много методов модуляции, которые классифицируются в зависимости от типа используемой модуляции. Из всех этих методов используется цифровая модуляция импульсно-кодовой модуляции (ИКМ) .

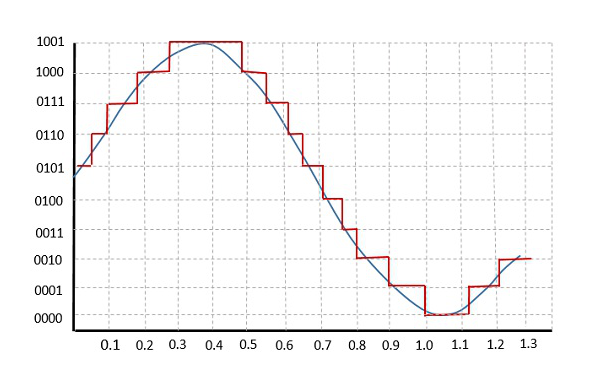
Сигнал подвергается импульсной кодовой модуляции для преобразования его аналоговой информации в двоичную последовательность, т. Е. 1 и 0 . Выход PCM будет напоминать двоичную последовательность. На следующем рисунке показан пример вывода ИКМ по отношению к мгновенным значениям данной синусоидальной волны.

Вместо последовательности импульсов PCM производит серию цифр или цифр, и поэтому этот процесс называется цифровым . Каждая из этих цифр, хотя и в двоичном коде, представляет приблизительную амплитуду выборки сигнала в этот момент.

В импульсной кодовой модуляции сигнал сообщения представлен последовательностью кодированных импульсов. Этот сигнал сообщения достигается путем представления сигнала в дискретной форме как по времени, так и по амплитуде.

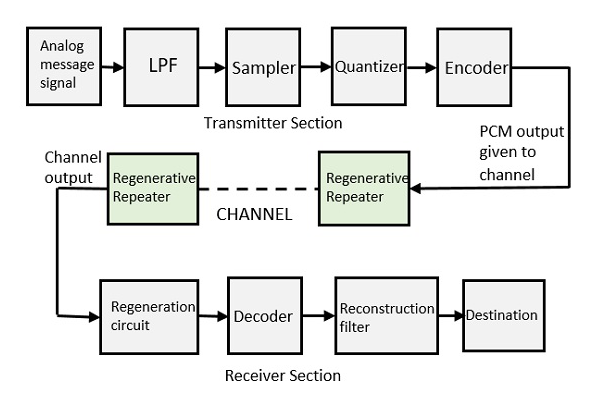
Основные элементы ПКМ

Секция передатчика схемы импульсного кода состоит из выборки, квантования и кодирования , которые выполняются в секции аналого-цифрового преобразователя. Фильтр нижних частот перед выборкой предотвращает наложение сигнала сообщения.

Основными операциями в секции приемника являются регенерация искаженных сигналов, декодирование и восстановление квантованной последовательности импульсов. Ниже приведена блок-схема PCM, которая представляет основные элементы секций передатчика и приемника.

Фильтр низких частот

Этот фильтр исключает высокочастотные составляющие, присутствующие во входном аналоговом сигнале, который превышает максимальную частоту сигнала сообщения, чтобы избежать наложения сигнала сообщения.

пробоотборник

Это метод, который помогает собирать данные выборки при мгновенных значениях сигнала сообщения, чтобы восстановить исходный сигнал. Частота дискретизации должна быть более чем в два раза больше, чем самая высокая частотная составляющая W сигнала сообщения, в соответствии с теоремой дискретизации.

квантователь

Квантование — это процесс уменьшения избыточных битов и ограничения данных. Выбранный выходной сигнал при передаче в Quantizer уменьшает избыточные биты и сжимает значение.

кодировщик

Оцифровка аналогового сигнала осуществляется кодером. Каждый квантованный уровень обозначается двоичным кодом. Выборка, сделанная здесь, является процессом выборки и удержания. Эти три секции (LPF, Sampler и Quantizer) будут действовать как аналого-цифровой преобразователь. Кодирование минимизирует используемую пропускную способность.

Регенеративный Повторитель

Этот раздел увеличивает уровень сигнала. Выход канала также имеет одну схему регенеративного повторителя, чтобы компенсировать потерю сигнала и реконструировать сигнал, а также увеличить его силу.

дешифратор

Схема декодера декодирует форму импульса с кодированием для воспроизведения исходного сигнала. Эта схема действует как демодулятор.

Фильтр реконструкции

После того, как цифроаналоговое преобразование выполнено регенеративной схемой и декодером, используется фильтр нижних частот, называемый фильтром восстановления, чтобы вернуть исходный сигнал.

Следовательно, схема модулятора импульсного кода оцифровывает данный аналоговый сигнал, кодирует его и дискретизирует, а затем передает его в аналоговой форме. Весь этот процесс повторяется в обратном порядке для получения исходного сигнала.

Цифровая связь — выборка

Выборка определяется как «Процесс измерения мгновенных значений непрерывного сигнала в дискретной форме».

Выборка — это фрагмент данных, взятый из целых данных, который непрерывен во временной области.

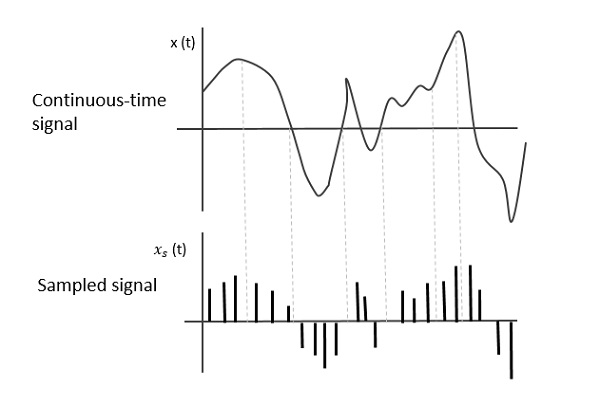
Когда источник генерирует аналоговый сигнал и если он должен быть оцифрован, имея 1 с и 0 с, то есть Высокий или Низкий, сигнал должен быть дискретизирован по времени. Эта дискретизация аналогового сигнала называется выборкой.

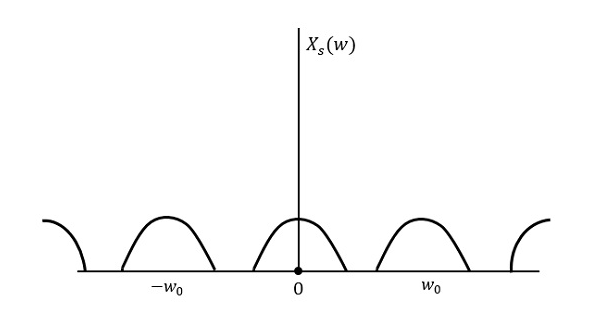
На следующем рисунке показан непрерывный сигнал x (t) и дискретизированный сигнал x _s (t) . Когда x (t) умножается на периодическую последовательность импульсов, получается дискретный сигнал x _s (t) .

Частота выборки

Чтобы дискретизировать сигналы, промежуток между выборками должен быть исправлен. Этот разрыв можно назвать периодом выборки T _s .

SamplingFrequency= frac1Ts=fs $$Sampling \: Frequency = \ frac {1} {T_ {s}} = f_s$$

Куда,

• $T_s$ — время выборки

• $f_s$ — частота дискретизации или частота дискретизации.

$T_s$ — время выборки

$f_s$ — частота дискретизации или частота дискретизации.

Частота выборки является обратной величиной периода выборки. Эту частоту дискретизации можно просто назвать частотой дискретизации . Частота дискретизации обозначает количество выборок в секунду или для конечного набора значений.

Для восстановления аналогового сигнала по оцифрованному сигналу частота дискретизации должна быть высоко оценена. Частота дискретизации должна быть такой, чтобы данные в сигнале сообщения не терялись и не перекрывались. Следовательно, ставка была фиксированной для этого, называемой скоростью Найквиста.

Рейтинг Найквиста

Предположим, что сигнал ограничен полосой частот без частотных составляющих выше, чем W герц. Это означает, что W — самая высокая частота. Для такого сигнала для эффективного воспроизведения исходного сигнала частота дискретизации должна быть в два раза выше самой высокой частоты.

Что значит,

$$f_S = 2W$$

Куда,

• $f_S$ — частота дискретизации

• W самая высокая частота

$f_S$ — частота дискретизации

W самая высокая частота

Эта частота дискретизации называется частотой Найквиста .

Была сформулирована теорема под названием «Теорема выборки» о теории скорости Найквиста.

Теорема выборки

Теорема отсчетов, которая также называется теоремой Найквиста , дает теорию достаточной частоты дискретизации в терминах полосы пропускания для класса функций с ограниченной полосой пропускания.

Теорема отсчетов гласит, что «сигнал может быть точно воспроизведен, если он дискретизируется с частотой f _s, которая в два раза превышает максимальную частоту W ».

Чтобы понять эту теорему отсчетов, давайте рассмотрим сигнал с ограниченной полосой частот, т. Е. Сигнал, значение которого не равно нулю между некоторыми значениями –W и W Герц.

Такой сигнал представляется как x(f)=0for midf mid>W$x (f) = 0 \: for \: \ mid f \ mid> W$

Для сигнала непрерывного времени x (t) , сигнала с ограниченной полосой частот в частотной области, можно представить, как показано на следующем рисунке.

Нам нужна частота выборки, частота, на которой не должно быть потери информации даже после выборки. Для этого у нас есть частота Найквиста, что частота дискретизации должна быть в два раза больше максимальной частоты. Это критическая частота выборки.

Если сигнал x (t) дискретизируется выше частоты Найквиста, исходный сигнал может быть восстановлен, а если он дискретизирован ниже частоты Найквиста, сигнал не может быть восстановлен.

На следующем рисунке поясняется сигнал, если он дискретизируется с более высокой скоростью, чем 2 Вт в частотной области.

На приведенном выше рисунке показано преобразование Фурье сигнала x _s (t) . Здесь информация воспроизводится без каких-либо потерь. Там нет путаницы и, следовательно, восстановление возможно.

Преобразование Фурье сигнала x _s (t)

$$X_s (w) = \ frac {1} {T_ {s}} \ sum_ {n = - \ infty} ^ \ infty X (w-nw_0)$$

Где $T_s$ = период выборки и $w_0 = \ frac {2 \ pi} {T_s}$

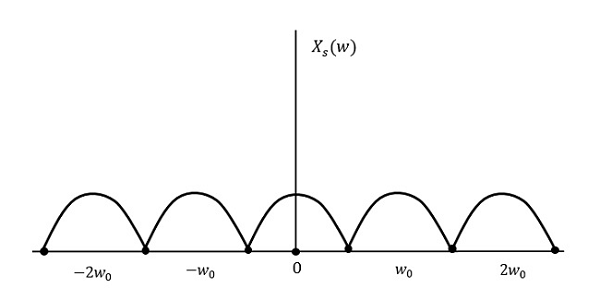
Давайте посмотрим, что произойдет, если частота дискретизации равна двойной максимальной частоте ( 2 Вт )

Это означает,

$$f_s = 2W$$

Куда,

• $f_s$ — частота дискретизации

• W самая высокая частота

$f_s$ — частота дискретизации

W самая высокая частота

Результат будет таким, как показано на рисунке выше. Информация заменяется без каких-либо потерь. Следовательно, это также хорошая частота дискретизации.

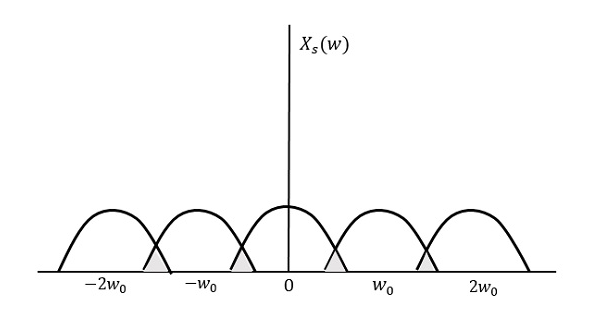
Теперь давайте посмотрим на состояние,

$$f_s <2W$$

Результирующий шаблон будет выглядеть следующим образом.

Из приведенного выше паттерна можно наблюдать, что происходит перекрытие информации, что приводит к смешению и потере информации. Это нежелательное явление перекрытия называется Aliasing.

Aliasing

Псевдоним может быть назван «явлением высокочастотного компонента в спектре сигнала, принимающего идентичность низкочастотного компонента в спектре его дискретизированной версии».

Корректирующие меры, принятые для уменьшения эффекта алиасинга, —

• В секции передатчика PCM перед сэмплером используется фильтр сглаживания нижних частот , чтобы устранить нежелательные высокочастотные компоненты.

• Сигнал, который дискретизируется после фильтрации, дискретизируется со скоростью, немного превышающей частоту Найквиста.

В секции передатчика PCM перед сэмплером используется фильтр сглаживания нижних частот , чтобы устранить нежелательные высокочастотные компоненты.

Сигнал, который дискретизируется после фильтрации, дискретизируется со скоростью, немного превышающей частоту Найквиста.

Этот выбор частоты дискретизации выше, чем частота Найквиста, также помогает упростить конструкцию фильтра восстановления в приемнике.

Область преобразования Фурье

Обычно наблюдается, что мы ищем помощи рядов Фурье и преобразований Фурье в анализе сигналов, а также в доказательстве теорем. Это потому что —

• Преобразование Фурье является расширением ряда Фурье для непериодических сигналов.

• Преобразование Фурье является мощным математическим инструментом, который помогает просматривать сигналы в разных областях и помогает легко анализировать сигналы.

• Любой сигнал может быть разложен по сумме синусов и косинусов с использованием этого преобразования Фурье.

Преобразование Фурье является расширением ряда Фурье для непериодических сигналов.

Преобразование Фурье является мощным математическим инструментом, который помогает просматривать сигналы в разных областях и помогает легко анализировать сигналы.

Любой сигнал может быть разложен по сумме синусов и косинусов с использованием этого преобразования Фурье.

В следующей главе давайте поговорим о концепции квантования.

Цифровая связь — квантование

Оцифровка аналоговых сигналов включает округление значений, которые приблизительно равны аналоговым значениям. Метод выборки выбирает несколько точек на аналоговом сигнале, а затем эти точки объединяются, чтобы округлить значение до почти стабилизированного значения. Такой процесс называется квантованием .

Квантование аналогового сигнала

Аналого-цифровые преобразователи выполняют функцию этого типа для создания серии цифровых значений из данного аналогового сигнала. На следующем рисунке представлен аналоговый сигнал. Этот сигнал, чтобы быть преобразованным в цифровой, должен пройти выборку и квантование.

Квантование аналогового сигнала выполняется путем дискретизации сигнала с несколькими уровнями квантования. Квантование представляет выборочные значения амплитуды с помощью конечного набора уровней, что означает преобразование выборки с непрерывной амплитудой в сигнал с дискретным временем.

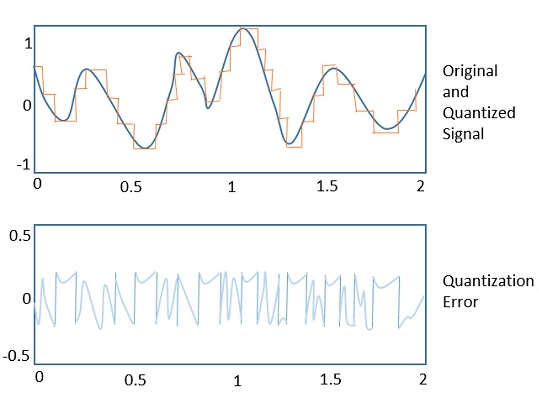
На следующем рисунке показано, как аналоговый сигнал квантуется. Синяя линия представляет аналоговый сигнал, а коричневая представляет квантованный сигнал.

Как выборка, так и квантование приводят к потере информации. Качество выходного сигнала квантователя зависит от количества используемых уровней квантования. Дискретные амплитуды квантованного выхода называются уровнями представления или уровнями восстановления . Интервал между двумя соседними уровнями представления называется квантовым или ступенчатым размером .

На следующем рисунке показан результирующий квантованный сигнал, который является цифровой формой для данного аналогового сигнала.

Это также называется волновой формой лестничной клетки, в соответствии с ее формой.

Типы квантования

Существует два типа квантования — равномерное квантование и неоднородное квантование.

Тип квантования, при котором уровни квантования расположены равномерно, называется равномерным квантованием . Тип квантования, при котором уровни квантования являются неравными, и главным образом соотношение между ними является логарифмическим, называется неравномерным квантованием .

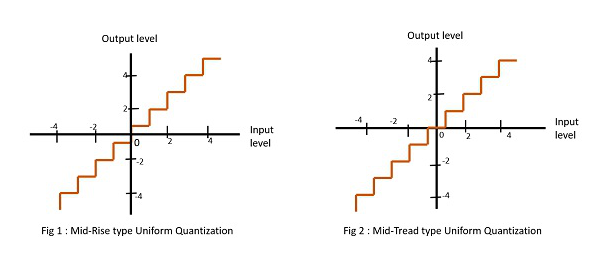
Существует два типа равномерного квантования. Это тип Mid-Rise и тип Mid-Tread. На следующих рисунках представлены два типа равномерного квантования.

На рисунке 1 показан тип среднего роста, а на рисунке 2 — тип среднего протектора с равномерным квантованием.

• Тип Mid-Rise назван так потому, что начало координат лежит в середине поднимающейся части лестничной клетки, такой как граф. Уровни квантования в этом типе чётные.

• Тип середины ступени называется так, потому что источник лежит в середине ступени лестничной клетки, как граф. Уровни квантования в этом типе нечетные по количеству.

• Как средние, так и средние протекторные типы однородных квантователей симметричны относительно происхождения.

Тип Mid-Rise назван так потому, что начало координат лежит в середине поднимающейся части лестничной клетки, такой как граф. Уровни квантования в этом типе чётные.

Тип середины ступени называется так, потому что источник лежит в середине ступени лестничной клетки, как граф. Уровни квантования в этом типе нечетные по количеству.

Как средние, так и средние протекторные типы однородных квантователей симметричны относительно происхождения.

Ошибка квантования

Для любой системы при ее функционировании всегда существует разница в значениях ее входа и выхода. Обработка системы приводит к ошибке, которая является разницей этих значений.

Разница между входным значением и его квантованным значением называется ошибкой квантования . Квантизатор — это логарифмическая функция, которая выполняет квантование (округление значения). Аналого-цифровой преобразователь ( АЦП ) работает как квантователь.

На следующем рисунке показан пример ошибки квантования, показывающий разницу между исходным сигналом и квантованным сигналом.

Шум квантования

Это тип ошибки квантования, который обычно возникает в аналоговом звуковом сигнале при квантовании его в цифровой. Например, в музыке сигналы постоянно меняются, где закономерность не обнаруживается в ошибках. Такие ошибки создают широкополосный шум, называемый шумом квантования .

Компандирование в PCM

Слово Companding — это комбинация Compressing и Expanding, что означает, что оно делает и то, и другое. Это нелинейный метод, используемый в PCM, который сжимает данные в передатчике и расширяет те же данные в приемнике. Эффекты шума и перекрестных помех уменьшаются при использовании этой техники.

Существует два типа техники компандирования. Они —

Техника компандирования по закону

• Равномерное квантование достигается при A = 1 , где характеристическая кривая является линейной и сжатие не выполняется.

• А-закон имеет средний рост в начале координат. Следовательно, он содержит ненулевое значение.

• Компандирование по закону используется для телефонных систем PCM.

Равномерное квантование достигается при A = 1 , где характеристическая кривая является линейной и сжатие не выполняется.

А-закон имеет средний рост в начале координат. Следовательно, он содержит ненулевое значение.

Компандирование по закону используется для телефонных систем PCM.

Техника Компандирования µ-закона

• Равномерное квантование достигается при µ = 0 , где характеристическая кривая является линейной и сжатие не выполняется.

• µ-закон имеет середину протектора в начале координат. Следовательно, он содержит нулевое значение.

• µ-закон компандирования используется для речевых и музыкальных сигналов.

Равномерное квантование достигается при µ = 0 , где характеристическая кривая является линейной и сжатие не выполняется.

µ-закон имеет середину протектора в начале координат. Следовательно, он содержит нулевое значение.

µ-закон компандирования используется для речевых и музыкальных сигналов.

µ-закон используется в Северной Америке и Японии.

Цифровая связь — дифференциальный PCM

Для семплов с высокой степенью корреляции при кодировании методом PCM оставьте избыточную информацию позади. Чтобы обработать эту избыточную информацию и получить лучший вывод, разумно принять прогнозируемое значение выборки, взятое из его предыдущего вывода, и суммировать их с квантованными значениями. Такой процесс называется техникой дифференциального PCM (DPCM) .

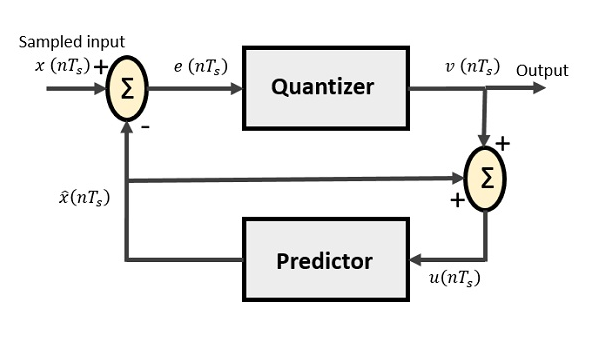
DPCM передатчик

Передатчик DPCM состоит из квантователя и предиктора с двумя летними цепями. Ниже приведена блок-схема передатчика DPCM.

Сигналы в каждой точке обозначаются как —

• $x (nT_s)$ — выборочный вход

• $\ widehat {x} (nT_s)$ — прогнозируемая выборка

• $e (nT_s)$ — это разность выборочных входных данных и прогнозируемых выходных данных, часто называемая ошибкой прогнозирования.

• $v (nT_s)$ — квантованный вывод

• $u (nT_s)$ — это входной сигнал предиктора, который на самом деле является летним выходом выходного сигнала предиктора и выходного сигнала квантователя.

$x (nT_s)$ — выборочный вход

$\ widehat {x} (nT_s)$ — прогнозируемая выборка

$e (nT_s)$ — это разность выборочных входных данных и прогнозируемых выходных данных, часто называемая ошибкой прогнозирования.

$v (nT_s)$ — квантованный вывод

$u (nT_s)$ — это входной сигнал предиктора, который на самом деле является летним выходом выходного сигнала предиктора и выходного сигнала квантователя.

Предиктор формирует предполагаемые выборки из предыдущих выходов схемы передатчика. Входными данными для этого предиктора являются квантованные версии входного сигнала $x (nT_s)$.

Выход квантователя представлен как —

$$v (nT_s) = Q [e (nT_s)]$$

$= e (nT_s) + q (nT_s)$

Где q (nT _s ) — ошибка квантования

Вход предиктора является суммой выходного сигнала квантователя и выходного сигнала предиктора,

$$u (nT_s) = \ widehat {x} (nT_s) + v (nT_s)$$

$u (nT_s) = \ widehat {x} (nT_s) + e (nT_s) + q (nT_s)$

$$u (nT_s) = x (nT_s) + q (nT_s)$$

Та же схема предиктора используется в декодере для восстановления исходного ввода.

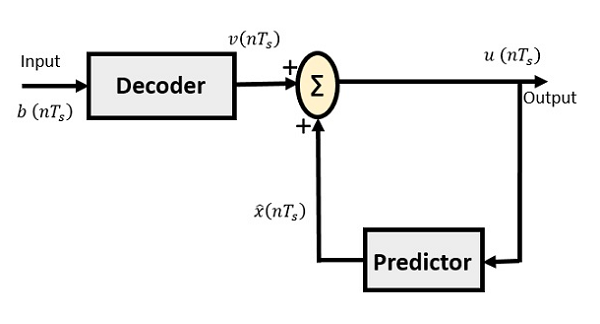
DPCM-приемник

Блок-схема приемника DPCM состоит из декодера, предиктора и летней схемы. Ниже приведена схема приемника DPCM.

Обозначение сигналов такое же, как и у предыдущих. При отсутствии шума кодированный вход приемника будет таким же, как кодированный выход передатчика.

Как упоминалось ранее, предиктор принимает значение, основанное на предыдущих выходных данных. Входные данные, данные декодеру, обрабатываются, и эти выходные данные суммируются с выходными данными предиктора, чтобы получить лучший выходной сигнал.

Цифровая связь — дельта-модуляция

Частота дискретизации сигнала должна быть выше, чем частота Найквиста, чтобы добиться лучшей дискретизации. Если этот интервал дискретизации в дифференциальной ИКМ значительно уменьшается, разность амплитуд между выборками очень мала, как если бы разность составляла 1-битовое квантование , тогда размер шага будет очень малым, то есть Δ (дельта).

Дельта-модуляция

Тип модуляции, где частота дискретизации намного выше и при которой размер шага после квантования имеет меньшее значение, такая модуляция называется дельта-модуляцией .

Особенности дельта-модуляции

Ниже приведены некоторые особенности дельта-модуляции.

• Вход с избыточной дискретизацией используется для полного использования корреляции сигнала.

• Дизайн квантования прост.

• Входная последовательность намного выше, чем скорость Найквиста.

• Качество умеренное.

• Конструкция модулятора и демодулятора проста.

• Лестничная аппроксимация выходного сигнала.

• Размер шага очень мал, т. Е. Δ (дельта).

• Скорость передачи данных может быть выбрана пользователем.

• Это предполагает более простую реализацию.

Вход с избыточной дискретизацией используется для полного использования корреляции сигнала.

Дизайн квантования прост.

Входная последовательность намного выше, чем скорость Найквиста.

Качество умеренное.

Конструкция модулятора и демодулятора проста.

Лестничная аппроксимация выходного сигнала.

Размер шага очень мал, т. Е. Δ (дельта).

Скорость передачи данных может быть выбрана пользователем.

Это предполагает более простую реализацию.

Дельта-модуляция — это упрощенная форма метода DPCM, также рассматриваемая как 1-битная схема DPCM . При уменьшении интервала выборки корреляция сигнала будет выше.

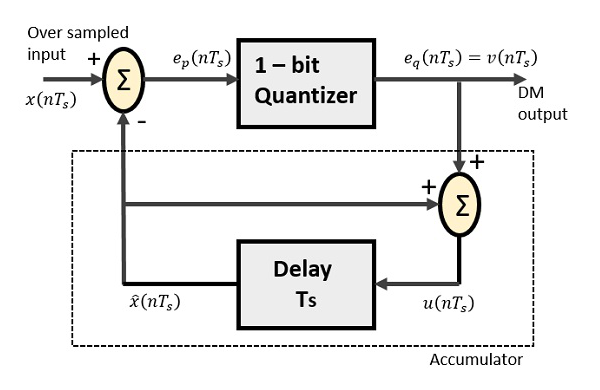
Дельта модулятор

Дельта-модулятор состоит из 1-битного квантователя и цепи задержки, а также двух летних цепей. Ниже приведена блок-схема дельта-модулятора.

Схема предиктора в DPCM заменяется простой схемой задержки в DM.

Из приведенной выше диаграммы мы имеем обозначения как —

• $x (nT_s)$ = более дискретный ввод

• $e_p (nT_s)$ = летний выход и вход квантователя

• $e_q (nT_s)$ = выход квантователя = $v (nT_s)$

• $\ widehat {x} (nT_s)$ = выход схемы задержки

• $u (nT_s)$ = вход цепи задержки

$x (nT_s)$ = более дискретный ввод

$e_p (nT_s)$ = летний выход и вход квантователя

$e_q (nT_s)$ = выход квантователя = $v (nT_s)$

$\ widehat {x} (nT_s)$ = выход схемы задержки

$u (nT_s)$ = вход цепи задержки

Используя эти обозначения, теперь мы попытаемся выяснить процесс дельта-модуляции.

$e_p (nT_s) = x (nT_s) - \ widehat {x} (nT_s)$

——— уравнение 1

$= x (nT_s) - u ([n - 1] T_s)$

$= x (nT_s) - [\ widehat {x} [[n - 1] T_s] + v [[n-1] T_s]]$

——— уравнение 2

В дальнейшем,

$v (nT_s) = e_q (nT_s) = S.sig. [e_p (nT_s)]$

——— уравнение 3

$u (nT_s) = \ widehat {x} (nT_s) + e_q (nT_s)$

Куда,

• $\ widehat {x} (nT_s)$ = предыдущее значение схемы задержки

• $e_q (nT_s)$ = выход квантователя = $v (nT_s)$

$\ widehat {x} (nT_s)$ = предыдущее значение схемы задержки

$e_q (nT_s)$ = выход квантователя = $v (nT_s)$

Следовательно,

$u (nT_s) = u ([n-1] T_s) + v (nT_s)$

——— уравнение 4

Что значит,

Настоящий вход блока задержки

= (Предыдущий выход блока задержки) + (текущий выход квантователя)

Предполагая нулевое условие накопления,

$u (nT_s) = S \ displaystyle \ sum \ limit_ {j = 1} ^ n сиг [e_p (jT_s)]$

Накопленная версия вывода DM = $\ displaystyle \ sum \ limit_ {j = 1} ^ nv (jT_s)$

——— уравнение 5

Теперь обратите внимание, что

$\ widehat {x} (nT_s) = u ([n-1] T_s)$

$= \ displaystyle \ sum \ limit_ {j = 1} ^ {n - 1} v (jT_s)$

——— уравнение 6

Выход блока задержки — это отставание выхода Аккумулятора на одну выборку.

Из уравнений 5 и 6 мы получаем возможную структуру для демодулятора.

Аппроксимированная форма волны в лестничной клетке будет выходом дельта-модулятора с размером шага в виде дельты ( Δ ). Качество выходного сигнала умеренное.

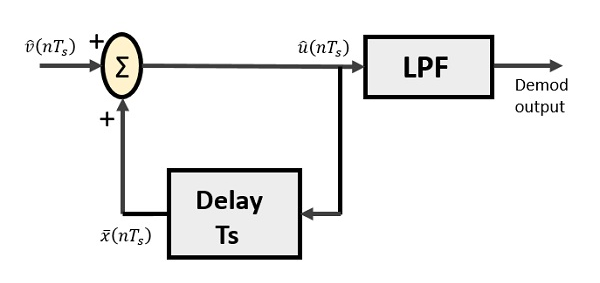
Дельта Демодулятор

Дельта-демодулятор состоит из фильтра нижних частот, летнего датчика и цепи задержки. Схема предиктора здесь исключена, и, следовательно, предполагаемый вход не поступает на демодулятор.

Ниже приведена схема для дельта-демодулятора.

Из приведенной выше диаграммы мы имеем обозначения как —

• $\ widehat {v} (nT_s)$ — входная выборка

• $\ widehat {u} (nT_s)$ — летний результат

• $\ bar {x} (nT_s)$ — задержанный вывод

$\ widehat {v} (nT_s)$ — входная выборка

$\ widehat {u} (nT_s)$ — летний результат

$\ bar {x} (nT_s)$ — задержанный вывод

Двоичная последовательность будет передана в качестве входа в демодулятор. Примерный выход лестничной клетки дан LPF.

Фильтр нижних частот используется по многим причинам, но основной причиной является устранение шума для внеполосных сигналов. Ошибка размера шага, которая может возникнуть в передатчике, называется зернистым шумом , который здесь исключается. Если шум отсутствует, то выход модулятора равен входу демодулятора.

Преимущества DM над DPCM

• 1-битный квантователь

• Очень легкая конструкция модулятора и демодулятора

1-битный квантователь

Очень легкая конструкция модулятора и демодулятора

Однако в DM существует некоторый шум.

• Искажение наклона при перегрузке (когда Δ мало)

• Зернистый шум (когда Δ велико)

Искажение наклона при перегрузке (когда Δ мало)

Зернистый шум (когда Δ велико)

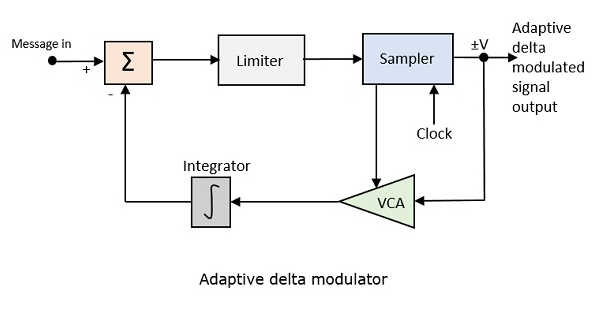
Адаптивная дельта-модуляция (ADM)

В цифровой модуляции мы столкнулись с определенной проблемой определения размера шага, который влияет на качество выходной волны.

Больший размер шага необходим в крутом наклоне модулирующего сигнала, а меньший размер шага необходим там, где сообщение имеет небольшой наклон. Мельчайшие детали упускаются в процессе. Таким образом, было бы лучше, если бы мы могли регулировать размер шага в соответствии с нашим требованием, чтобы получить выборку желаемым способом. Это концепция адаптивной дельта-модуляции .

Ниже приведена блок-схема адаптивного дельта-модулятора.

Усиление усилителя, управляемого напряжением, регулируется выходным сигналом сэмплера. Усиление усилителя определяет размер шага, и оба пропорциональны.

ADM квантует разницу между значением текущей выборки и прогнозируемой величиной следующей выборки. Он использует переменную высоту шага для прогнозирования следующих значений для точного воспроизведения быстро меняющихся значений.

Цифровая связь — техника

Есть несколько методов, которые проложили основной путь к цифровым коммуникационным процессам. Для оцифровки сигналов у нас есть методы дискретизации и квантования.

Чтобы они были представлены математически, у нас есть технологии LPC и цифрового мультиплексирования. Эти методы цифровой модуляции дополнительно обсуждаются.

Линейное прогнозирующее кодирование

Линейное прогнозирующее кодирование (LPC) — это инструмент, который представляет цифровые речевые сигналы в модели линейного прогнозирования. Это в основном используется при обработке аудиосигналов, синтезе речи, распознавании речи и т. Д.

Линейное предсказание основано на идее, что текущая выборка основана на линейной комбинации прошлых выборок. Анализ оценивает значения сигнала с дискретным временем как линейную функцию предыдущих выборок.

Спектральная огибающая представляется в сжатом виде, используя информацию линейной прогнозирующей модели. Это может быть математически представлено как —

$s (n) = \ displaystyle \ sum \ limit_ {k = 1} ^ p \ alpha_k s (n - k)$ для некоторого значения p и α _k

куда

• s (n) — текущий образец речи

• к конкретный образец

• р является самым последним значением

• α _k — коэффициент предиктора

• s (n — k) — предыдущий образец речи

s (n) — текущий образец речи

к конкретный образец

р является самым последним значением

α _k — коэффициент предиктора

s (n — k) — предыдущий образец речи

Для LPC значения коэффициента предиктора определяются путем минимизации суммы квадратов разностей (за конечный интервал) между фактическими речевыми выборками и линейно предсказанными.

Это очень полезный метод для кодирования речи с низкой скоростью передачи данных. Метод LPC очень близок к методу быстрого преобразования Фурье (FFT) .

мультиплексирование

Мультиплексирование — это процесс объединения нескольких сигналов в один сигнал через общую среду. Эти сигналы, если они аналоговые по своей природе, этот процесс называется аналоговым мультиплексированием . Если цифровые сигналы мультиплексируются, это называется цифровым мультиплексированием .

Мультиплексирование впервые было разработано в телефонии. Ряд сигналов были объединены для отправки по одному кабелю. Процесс мультиплексирования делит канал связи на несколько логических каналов, выделяя каждый канал для другого сигнала сообщения или потока данных для передачи. Устройство, которое выполняет мультиплексирование, может называться MUX . Обратный процесс, т. Е. Извлечение количества каналов из одного, что выполняется в приемнике, называется демультиплексированием . Устройство, которое выполняет демультиплексирование, называется DEMUX .

Следующие цифры представляют MUX и DEMUX. Их основное использование в области связи.

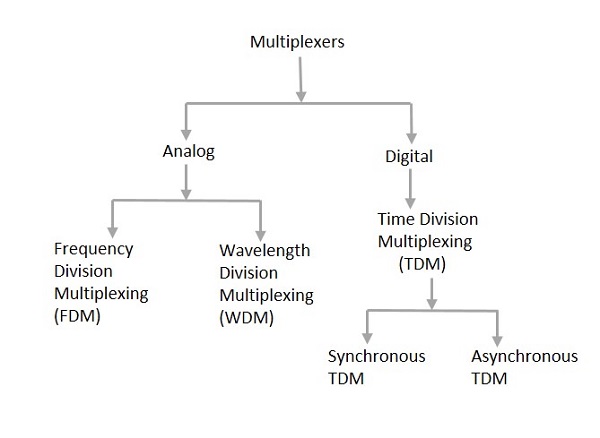
Типы мультиплексоров

Существует в основном два типа мультиплексоров, а именно аналоговый и цифровой. Они также делятся на FDM, WDM и TDM. Следующий рисунок дает подробное представление об этой классификации.

На самом деле, существует много типов методов мультиплексирования. Из них все мы имеем основные типы с общей классификацией, упомянутые на рисунке выше.

Аналоговое мультиплексирование

Методы аналогового мультиплексирования включают сигналы, которые являются аналоговыми по своей природе. Аналоговые сигналы мультиплексируются в соответствии с их частотой (FDM) или длиной волны (WDM).

Мультиплексирование с частотным разделением (FDM)

В аналоговом мультиплексировании наиболее часто используемым методом является мультиплексирование с частотным разделением (FDM) . Этот метод использует различные частоты для объединения потоков данных, для отправки их на коммуникационную среду, в виде единого сигнала.

Пример . Традиционный телевизионный передатчик, который передает несколько каналов по одному кабелю, использует FDM.

Мультиплексирование с разделением по длине волны (WDM)

Мультиплексирование с разделением по длине волны представляет собой аналоговый метод, в котором множество потоков данных с различными длинами волн передаются в световом спектре. Если длина волны увеличивается, частота сигнала уменьшается. Призма, которая может превращать волны различной длины в одну линию, может использоваться на выходе MUX и входе DEMUX.

Пример. В оптоволоконной связи используется метод WDM для объединения различных длин волн в один источник света для связи.

Цифровое мультиплексирование

Термин цифровой представляет дискретные биты информации. Следовательно, доступные данные находятся в форме кадров или пакетов, которые являются дискретными.

Мультиплексирование с временным разделением (TDM)

В TDM временные рамки делятся на временные интервалы. Этот метод используется для передачи сигнала по одному каналу связи путем выделения одного интервала для каждого сообщения.

Из всех типов TDM основными являются синхронный и асинхронный TDM.

Синхронный TDM

В синхронном TDM вход подключен к кадру. Если имеется n соединений, то кадр делится на n слотов. Один слот выделяется для каждой входной линии.

В этом методе частота дискретизации является общей для всех сигналов и, следовательно, задается один и тот же тактовый вход. MUX постоянно выделяет один и тот же слот каждому устройству.

Асинхронный TDM

В асинхронном TDM частота дискретизации отличается для каждого из сигналов, и общий тактовый генератор не требуется. Если выделенное устройство в течение временного интервала ничего не передает и бездействует, то этот слот выделяется другому устройству, в отличие от синхронного. Этот тип TDM используется в сетях с асинхронным режимом передачи.

Регенеративный Повторитель

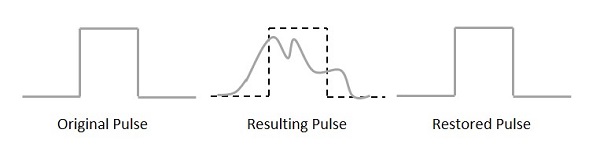
Чтобы любая система связи была надежной, она должна передавать и принимать сигналы эффективно, без потерь. Волна PCM после передачи по каналу искажается из-за шума, вносимого каналом.

Регенеративный импульс по сравнению с исходным и полученным импульсом будет таким, как показано на следующем рисунке.

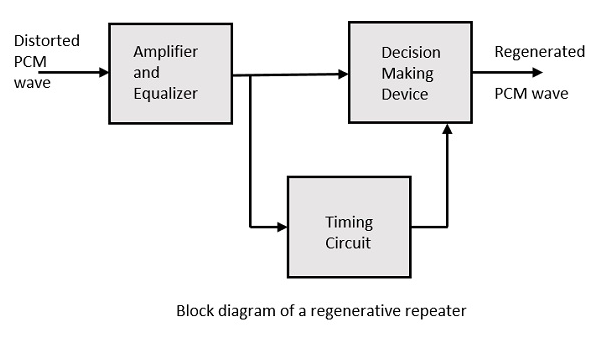
Для лучшего воспроизведения сигнала в тракте перед приемником используется схема, называемая регенеративным повторителем . Это помогает восстановить сигналы от произошедших потерь. Ниже приведено схематическое изображение.

Он состоит из эквалайзера, усилителя, схемы синхронизации и устройства для принятия решений. Их работа каждого из компонентов подробно описана ниже.

Эквалайзер

Канал производит амплитудные и фазовые искажения для сигналов. Это связано с характеристиками передачи канала. Схема эквалайзера компенсирует эти потери путем формирования принятых импульсов.

Цепь времени

Для получения качественного выхода выборка импульсов должна выполняться там, где отношение сигнал / шум (ОСШ) является максимальным. Для достижения этой идеальной выборки периодическая последовательность импульсов должна быть получена из принятых импульсов, что выполняется схемой синхронизации.

Следовательно, схема синхронизации выделяет интервал синхронизации для выборки при высоком SNR посредством принятых импульсов.

Устройство принятия решений

Схема синхронизации определяет время выборки. Устройство принятия решения включено в эти времена выборки. Устройство принятия решения определяет свой выходной сигнал на основе того, превышает ли амплитуда квантованного импульса и шум заранее установленное значение или нет.

Это несколько методов, используемых в цифровой связи. Есть и другие важные методы, которые необходимо изучить, называемые методами кодирования данных. Давайте узнаем о них в следующих главах, после того как взглянем на строковые коды.

Цифровая связь — линейные коды

Линейный код — это код, используемый для передачи данных цифрового сигнала по линии передачи. Этот процесс кодирования выбирается таким образом, чтобы избежать наложения и искажения сигнала, таких как межсимвольные помехи.

Свойства линейного кодирования

Ниже приведены свойства линейного кодирования —

• Поскольку кодирование выполняется для передачи большего количества битов в одном сигнале, используемая ширина полосы значительно уменьшается.

• Для данной полосы пропускания мощность используется эффективно.

• Вероятность ошибки значительно снижается.

• Обнаружение ошибок сделано, и биполярный также имеет возможность исправления.

• Плотность мощности очень благоприятная.

• Содержание времени является адекватным.

• Длинные строки 1 и 0 избегают, чтобы сохранить прозрачность.

Поскольку кодирование выполняется для передачи большего количества битов в одном сигнале, используемая ширина полосы значительно уменьшается.

Для данной полосы пропускания мощность используется эффективно.

Вероятность ошибки значительно снижается.

Обнаружение ошибок сделано, и биполярный также имеет возможность исправления.

Плотность мощности очень благоприятная.

Содержание времени является адекватным.

Длинные строки 1 и 0 избегают, чтобы сохранить прозрачность.

Типы линейного кодирования

Есть 3 типа линейного кодирования

• униполярный
• полярный
• Би-полярный

Униполярный сигнал

Однополярная сигнализация также называется включением-выключением или просто OOK .

Наличие импульса представляет собой 1, а отсутствие импульса представляет собой 0 .

Существует две разновидности униполярной сигнализации:

• Невозврат в ноль (NRZ)
• Возвращение к нулю (RZ)

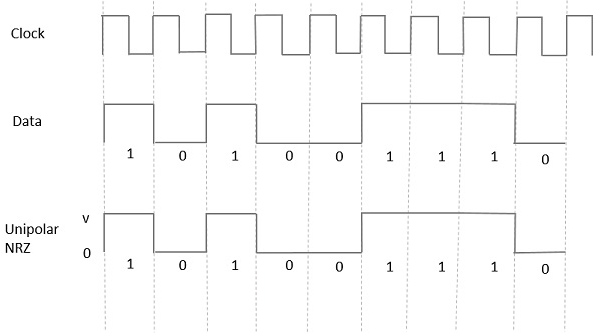
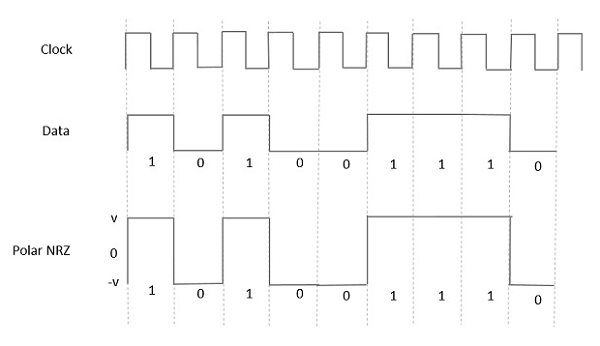
Униполярный невозврат в ноль (NRZ)

В этом типе однополярной сигнализации высокий уровень данных представлен положительным импульсом, называемым меткой , который имеет длительность T _0, равную длительности бит символа. Низкий входной сигнал не имеет импульса.

Следующий рисунок ясно показывает это.

преимущества

Преимущества Unipolar NRZ —

• Это просто.
• Требуется меньшая пропускная способность.

Недостатки

Недостатками Униполярного НРЗ являются —

• Исправление ошибок не производится.

• Присутствие низкочастотных компонентов может привести к снижению сигнала.

• Нет часов нет.

• Возможна потеря синхронизации (особенно для длинных строк 1 и 0 ).

Исправление ошибок не производится.

Присутствие низкочастотных компонентов может привести к снижению сигнала.

Нет часов нет.

Возможна потеря синхронизации (особенно для длинных строк 1 и 0 ).

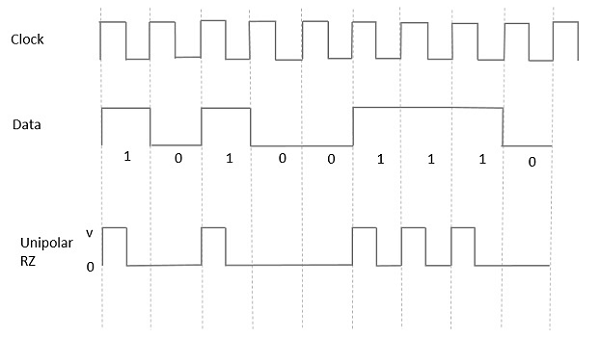
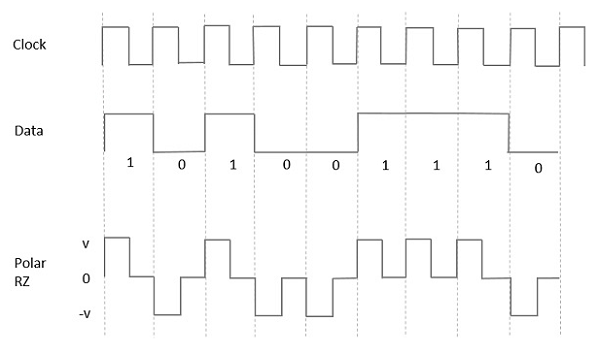
Униполярный возврат в ноль (RZ)

В этом типе униполярной сигнализации, высокого уровня данных, хотя он представлен импульсом Марка , его длительность T ₀ меньше, чем длительность бит символа. Половина битовой длительности остается высокой, но она немедленно возвращается к нулю и показывает отсутствие импульса в течение оставшейся половины битовой длительности.

Это ясно понять с помощью следующего рисунка.

преимущества

Преимущества Unipolar RZ —

• Это просто.
• Спектральная линия, присутствующая на скорости передачи символов, может использоваться в качестве часов.

Недостатки

Недостатками Unipolar RZ являются —

• Нет исправления ошибок.
• Занимает вдвое большую пропускную способность, чем униполярный NRZ.
• Снижение сигнала происходит в местах, где сигнал ненулевой при 0 Гц.

Полярная Сигнализация

Существует два метода полярной сигнализации. Они —

• Полярный НРЗ
• Полярный РЗ

Полярный НРЗ

В этом типе передачи сигналов Polar максимум данных представлен положительным импульсом, а минимум данных представлен отрицательным импульсом. На следующем рисунке это хорошо видно.

преимущества

Преимущества Polar NRZ —

• Это просто.
• Низкочастотных компонентов нет.

Недостатки

Недостатками Полярного НРЗ являются —

• Нет исправления ошибок.

• Нет часов нет.

• Снижение сигнала происходит в местах, где сигнал ненулевой при 0 Гц .

Нет исправления ошибок.

Нет часов нет.

Снижение сигнала происходит в местах, где сигнал ненулевой при 0 Гц .

Полярный РЗ

В этом типе сигнализации Polar, High в данных, хотя они представлены импульсом Mark , его длительность T ₀ меньше, чем длительность бит символа. Половина битовой длительности остается высокой, но она немедленно возвращается к нулю и показывает отсутствие импульса в течение оставшейся половины битовой длительности.

Тем не менее, для входного сигнала Low, отрицательный импульс представляет данные, и нулевой уровень остается тем же самым в течение другой половины битовой длительности. На следующем рисунке это ясно видно.

преимущества

Преимущества Polar RZ —

• Это просто.
• Низкочастотных компонентов нет.

Недостатки

Недостатками Polar RZ являются —

• Нет исправления ошибок.

• Нет часов нет.

• Занимает вдвое большую пропускную способность Полярного НРЗ.

• Снижение сигнала происходит в местах, где сигнал ненулевой при 0 Гц .

Нет исправления ошибок.

Нет часов нет.

Занимает вдвое большую пропускную способность Полярного НРЗ.

Снижение сигнала происходит в местах, где сигнал ненулевой при 0 Гц .

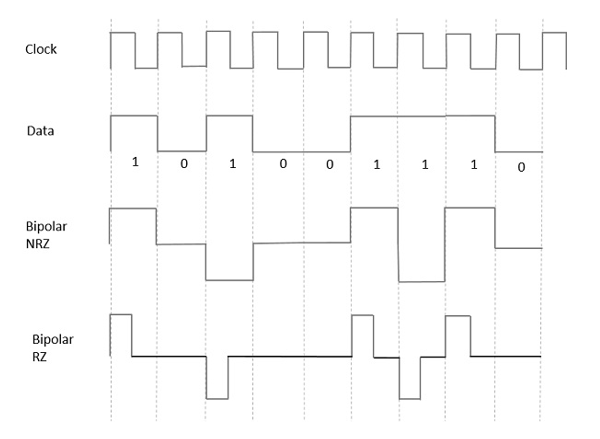
Биполярная Сигнализация

Это метод кодирования, который имеет три уровня напряжения, а именно +, — и 0 . Такой сигнал называется двойным двоичным сигналом .

Примером этого типа является Alverate Mark Inversion (AMI) . Для 1 уровень напряжения получает переход от + к — или от — к +, имеющий чередующиеся 1 с равной полярности. 0 будет иметь нулевой уровень напряжения.

Даже в этом методе у нас есть два типа.

• Биполярный НРЗ
• Биполярный рз

Из моделей, которые мы обсуждали, мы узнали разницу между NRZ и RZ. Здесь тоже все точно так же. Следующий рисунок ясно показывает это.

На приведенном выше рисунке представлены как биполярные сигналы NRZ, так и RZ. Длительность импульса и длительность символа в битах равны в типе NRZ, а длительность импульса составляет половину длительности символа в типе RZ.

преимущества

Ниже приведены преимущества —

• Это просто.

• Низкочастотных компонентов нет.

• Занимает меньшую пропускную способность, чем униполярные и полярные схемы NRZ.

• Этот метод подходит для передачи по соединенным линиям переменного тока, поскольку снижение сигнала здесь не происходит.

• В этом есть возможность обнаружения одной ошибки.

Это просто.

Низкочастотных компонентов нет.

Занимает меньшую пропускную способность, чем униполярные и полярные схемы NRZ.

Этот метод подходит для передачи по соединенным линиям переменного тока, поскольку снижение сигнала здесь не происходит.

В этом есть возможность обнаружения одной ошибки.

Недостатки

Ниже приведены недостатки —

• Нет часов нет.
• Длинные строки данных приводят к потере синхронизации.

Спектральная плотность мощности

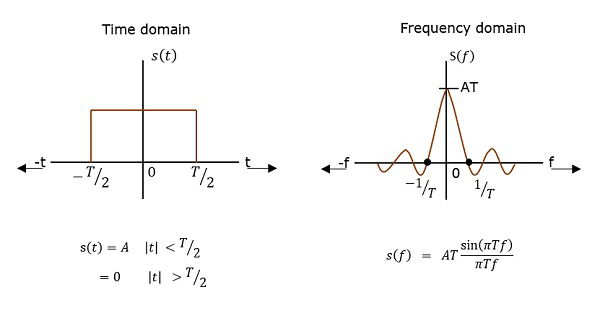
Функция, которая описывает, как мощность сигнала распределяется на различных частотах в частотной области, называется спектральной плотностью мощности (PSD) .

PSD — это Фурье-преобразование автокорреляции (сходство между наблюдениями). Это в форме прямоугольного импульса.

PSD Вывод

Согласно теореме Эйнштейна-Винера-Хинчина, если известна автокорреляционная функция или спектральная плотность мощности случайного процесса, точно можно найти другую.

Следовательно, для получения спектральной плотности мощности мы будем использовать временную автокорреляцию $(R_x (\ tau))$ сигнала мощности $x (t)$, как показано ниже.

$R_x (\ tau) = \ lim_ {T_p \ rightarrow \ infty} \ frac {1} {T_p} \ int _ {\ frac {{- T_p}} {2}} ^ {\ frac {T_p} {2}} x (t) x (t + \ tau) dt$

Поскольку $x (t)$ состоит из импульсов, $R_x (\ tau)$ можно записать в виде

$R_x (\ tau) = \ frac {1} {T} \ displaystyle \ sum \ limit_ {n = - \ infty} ^ \ infty R_n \ delta (\ tau - nT)$

Где $R_n = \ lim_ {N \ rightarrow \ infty} \ frac {1} {N} \ sum_ka_ka_ {k + n}$

Узнав, что $R_n = R _ {- n}$ для реальных сигналов, мы имеем

$S_x (w) = \ frac {1} {T} (R_0 + 2 \ displaystyle \ sum \ limit_ {n = 1} ^ \ infty R_n \ cos nwT)$

Поскольку импульсный фильтр имеет спектр $(w) \ leftrightarrow f (t)$, мы имеем

$s_y (w) = \ mid F (w) \ mid ^ 2S_x (w)$

$= \ frac {\ mid F (w) \ mid ^ 2} {T} (\ displaystyle \ sum \ limit_ {n = - \ infty} ^ \ infty R_ne ^ {- jnwT_ {b}})$

$= \ frac {\ mid F (w) \ mid ^ 2} {T} (R_0 + 2 \ displaystyle \ sum \ limit_ {n = 1} ^ \ infty R_n \ cos nwT)$

Отсюда получаем уравнение для спектральной плотности мощности. Используя это, мы можем найти PSD различных линейных кодов.

Методы кодирования данных

Кодирование — это процесс преобразования данных или заданной последовательности символов, символов, алфавитов и т. Д. В определенный формат для защищенной передачи данных. Декодирование — это обратный процесс кодирования, который заключается в извлечении информации из преобразованного формата.

Кодировка данных

Кодирование — это процесс использования различных комбинаций уровней напряжения или тока для представления единиц и нулей цифровых сигналов в линии передачи.

Распространенными типами кодирования линий являются униполярный, полярный, биполярный и манчестерский.

Методы кодирования

Метод кодирования данных подразделяется на следующие типы в зависимости от типа преобразования данных.

• Аналоговые данные для аналоговых сигналов. К этой категории относятся методы модуляции, такие как амплитудная модуляция, частотная модуляция и фазовая модуляция аналоговых сигналов.

• Аналоговые данные для цифровых сигналов. Этот процесс можно назвать оцифровкой, которая осуществляется с помощью импульсной кодовой модуляции (PCM). Следовательно, это не что иное, как цифровая модуляция. Как мы уже обсуждали, выборка и квантование являются важными факторами в этом. Дельта-модуляция дает лучшую производительность, чем PCM.

• Цифровые данные в аналоговые сигналы . Методы модуляции, такие как амплитудная манипуляция (ASK), частотная манипуляция (FSK), фазовая манипуляция (PSK) и т. Д., Подпадают под эту категорию. Они будут обсуждаться в последующих главах.

• Цифровые данные в цифровые сигналы — это в этом разделе. Есть несколько способов отобразить цифровые данные на цифровые сигналы. Некоторые из них —

Аналоговые данные для аналоговых сигналов. К этой категории относятся методы модуляции, такие как амплитудная модуляция, частотная модуляция и фазовая модуляция аналоговых сигналов.

Аналоговые данные для цифровых сигналов. Этот процесс можно назвать оцифровкой, которая осуществляется с помощью импульсной кодовой модуляции (PCM). Следовательно, это не что иное, как цифровая модуляция. Как мы уже обсуждали, выборка и квантование являются важными факторами в этом. Дельта-модуляция дает лучшую производительность, чем PCM.

Цифровые данные в аналоговые сигналы . Методы модуляции, такие как амплитудная манипуляция (ASK), частотная манипуляция (FSK), фазовая манипуляция (PSK) и т. Д., Подпадают под эту категорию. Они будут обсуждаться в последующих главах.

Цифровые данные в цифровые сигналы — это в этом разделе. Есть несколько способов отобразить цифровые данные на цифровые сигналы. Некоторые из них —

Невозврат в ноль (NRZ)

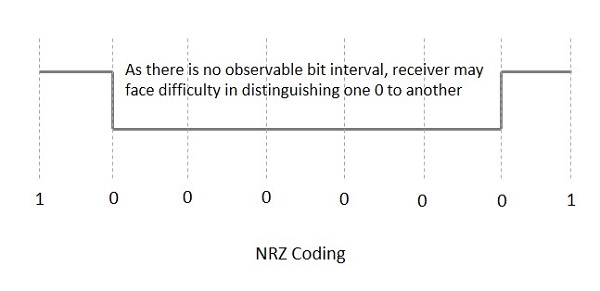
Коды NRZ имеют 1 для высокого уровня напряжения и 0 для низкого уровня напряжения. Основное поведение кодов NRZ состоит в том, что уровень напряжения остается постоянным в течение битового интервала. Конец или начало бита не будут указываться, и он будет поддерживать одно и то же состояние напряжения, если значение предыдущего бита и значение текущего бита совпадают.

На следующем рисунке поясняется концепция кодирования NRZ.

Если рассмотрен вышеприведенный пример, поскольку имеется длинная последовательность постоянного уровня напряжения, и тактовая синхронизация может быть потеряна из-за отсутствия битового интервала, приемнику становится трудно различать 0 и 1.

Есть два варианта в NRZ, а именно —

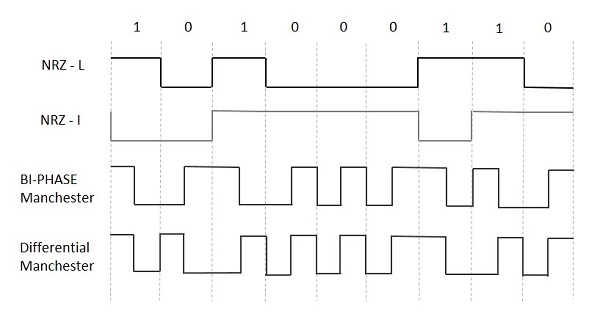
NRZ — L (NRZ — УРОВЕНЬ)

Полярность сигнала изменяется, только когда входной сигнал изменяется с 1 на 0 или с 0 на 1. Он такой же, как NRZ, однако первый бит входного сигнала должен иметь изменение полярности.

NRZ — I (NRZ — INVERTED)

Если 1 появляется во входящем сигнале, то происходит переход в начале битового интервала. Для 0 во входящем сигнале нет перехода в начале битового интервала.

Коды NRZ имеют недостаток , заключающийся в том, что синхронизация часов передатчика с часами приемника полностью нарушается, когда есть строка 1 с и 0 с . Следовательно, должна быть предусмотрена отдельная линия часов.

Двухфазное кодирование

Уровень сигнала проверяется дважды для каждого бита, как в начале, так и в середине. Следовательно, тактовая частота вдвое превышает скорость передачи данных, и, таким образом, частота модуляции также удваивается. Часы взяты из самого сигнала. Ширина полосы, необходимая для этого кодирования, больше.

Существует два типа двухфазного кодирования.

• Бифазный Манчестер
• Дифференциальный Манчестер

Бифазный Манчестер

В этом типе кодирования переход выполняется в середине битового интервала. Переход для результирующего импульса происходит от высокого к низкому в середине интервала для входного бита 1. В то время как переход от низкого к высокому для входного бита 0 .

Дифференциальный Манчестер

В этом типе кодирования всегда происходит переход в середине битового интервала. Если в начале битового интервала происходит переход, то входной бит равен 0 . Если в начале битового интервала перехода не происходит, то входной бит равен 1 .

На следующем рисунке показаны формы сигналов кодирования NRZ-L, NRZ-I, двухфазного Манчестера и дифференциального Манчестера для различных цифровых входов.

Блочное кодирование

Среди типов блочного кодирования известны следующие: кодирование 4B / 5B и кодирование 8B / 6T. Количество битов обрабатывается по-разному, в обоих этих процессах.

4B / 5B Кодировка

В манчестерском кодировании для отправки данных требуются часы с двойной скоростью, а не кодирование NRZ. Здесь, как следует из названия, 4 бита кода отображаются с 5 битами с минимальным количеством 1 бит в группе.

Проблема синхронизации часов в кодировании NRZ-I устраняется путем назначения эквивалентного слова из 5 битов вместо каждого блока из 4 последовательных битов. Эти 5-битные слова предопределены в словаре.

Основная идея выбора 5-битного кода состоит в том, что он должен иметь один ведущий 0 и не более двух конечных 0 . Следовательно, эти слова выбираются так, что в каждом блоке битов происходят две транзакции.

8B / 6T Кодировка

Мы использовали два уровня напряжения для передачи одного бита по одному сигналу. Но если мы используем более 3 уровней напряжения, мы можем отправлять больше битов на сигнал.

Например, если 6 уровней напряжения используются для представления 8 битов в одном сигнале, то такое кодирование называется кодированием 8B / 6T. Следовательно, в этом методе мы имеем целых 729 (3 ^ 6) комбинаций для сигнала и 256 (2 ^ 8) комбинаций для битов.

Эти методы в основном используются для преобразования цифровых данных в цифровые сигналы путем их сжатия или кодирования для надежной передачи данных.

Цифровая связь — Формирование импульса

После прохождения различных типов методов кодирования у нас есть представление о том, как данные подвержены искажениям и как принимаются меры, чтобы предотвратить их воздействие, чтобы установить надежную связь.

Есть еще одно важное искажение, которое наиболее вероятно может возникнуть, называемое межсимвольным вмешательством (ISI) .

Интерсимволы

Это форма искажения сигнала, при которой один или несколько символов мешают последующим сигналам, вызывая шум или обеспечивая плохой выходной сигнал.

Причины ISI

Основными причинами ISI являются —

• Многолучевое распространение
• Нелинейная частота в каналах

ISI нежелателен и должен быть полностью исключен, чтобы получить чистый вывод. Причины ISI также должны быть решены, чтобы уменьшить его эффект.

Чтобы просмотреть ISI в математической форме, присутствующей на выходе приемника, мы можем рассмотреть выход приемника.

Выходной сигнал принимающего фильтра $y (t)$ выбирается в момент времени $t_i = iT_b$ (где i принимает целочисленные значения), получая —

$y (t_i) = \ mu \ displaystyle \ sum \ limit_ {k = - \ infty} ^ {\ infty} a_kp (iT_b - kT_b)$

= muai+ mu displaystyle sum limit inftyk=− inftyk neqiakp(iTb−kTb)$= \ mu a_i + \ mu \ displaystyle \ sum \ limit_ {k = - \ infty \\ k \ neq i} ^ {\ infty} a_kp (iT_b - kT_b)$

В приведенном выше уравнении первый член $\ mu a_i$ создается i- ^м переданным битом.

Второе слагаемое представляет остаточное влияние всех других переданных битов на декодирование i- ^го бита. Этот остаточный эффект называется Inter Symbol Symbol Interference .

В отсутствие ISI, выход будет —

$$y (t_i) = \ mu a_i$$

Это уравнение показывает, что i- ^й переданный бит корректно воспроизводится. Однако наличие ISI вносит битовые ошибки и искажения в вывод.

При проектировании передатчика или приемника важно минимизировать влияние ISI, чтобы получать выходные данные с наименьшей вероятностью появления ошибок.

Коррелятивное кодирование

До сих пор мы обсуждали, что ISI является нежелательным явлением и ухудшает сигнал. Но тот же ISI, если его использовать контролируемым образом, позволяет достичь скорости передачи битов 2 Вт в секунду в канале с шириной полосы W Герц. Такая схема называется схемами сигнализации с корреляционным кодированием или частичным откликом .

Поскольку количество ISI известно, приемник легко спроектировать в соответствии с требованием, чтобы избежать влияния ISI на сигнал. Основная идея корреляционного кодирования достигается путем рассмотрения примера двоичной сигнализации .

Двоично-двоичная сигнализация

Название duo-binary означает удвоение пропускной способности двоичной системы. Чтобы понять это, рассмотрим двоичную входную последовательность {a _k }, состоящую из некоррелированных двоичных цифр, каждая из которых имеет длительность T _a . При этом сигнал 1 представлен +1 вольт, а символ 0 — -1 вольт.

Следовательно, выходные данные двоичного двоичного кодера c _k задаются как сумма существующей двоичной цифры a _k и предыдущего значения a _k-1, как показано в следующем уравнении.

$$c_k = a_k + a_ {k-1}$$

Вышеупомянутое уравнение гласит, что входная последовательность некоррелированной двоичной последовательности {a _k } изменяется на последовательность коррелированных трех импульсов уровня {c _k } . Эта корреляция между импульсами может быть понята как введение ISI в передаваемый сигнал искусственным образом.

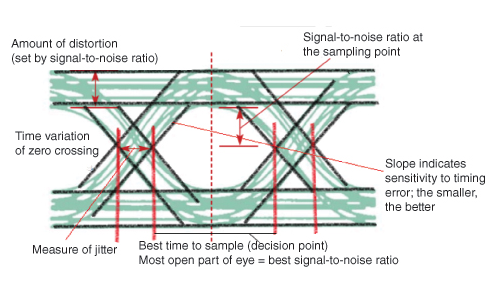
Глаз шаблон

Эффективным способом изучения эффектов ISI является паттерн глаз . Название Eye Pattern было дано из-за его сходства с человеческим глазом для бинарных волн. Внутренняя область рисунка глаза называется открытием глаза . На следующем рисунке показано изображение рисунка глаза.

Джиттер — это кратковременное отклонение момента цифрового сигнала от его идеального положения, которое может привести к ошибкам в данных.

Когда эффект ISI увеличивается, следы от верхней части к нижней части глазного отверстия увеличиваются, и глаз становится полностью закрытым, если ISI очень высокий.

Шаблон глаза предоставляет следующую информацию о конкретной системе.

• Фактические диаграммы зрения используются для оценки частоты ошибок по битам и отношения сигнал / шум.

• Ширина глазного отверстия определяет интервал времени, в течение которого принятая волна может быть дискретизирована без ошибок из ISI.

• Момент времени, когда глазное отверстие широко, будет предпочтительным временем для отбора проб.

• Частота закрытия глаза, в зависимости от времени выборки, определяет, насколько система чувствительна к ошибке синхронизации.

• Высота отверстия глаза в указанное время выборки определяет запас по шуму.

Фактические диаграммы зрения используются для оценки частоты ошибок по битам и отношения сигнал / шум.

Ширина глазного отверстия определяет интервал времени, в течение которого принятая волна может быть дискретизирована без ошибок из ISI.

Момент времени, когда глазное отверстие широко, будет предпочтительным временем для отбора проб.

Частота закрытия глаза, в зависимости от времени выборки, определяет, насколько система чувствительна к ошибке синхронизации.

Высота отверстия глаза в указанное время выборки определяет запас по шуму.

Следовательно, интерпретация структуры глаза является важным фактором.

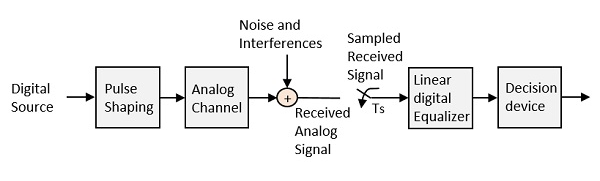
уравнивание

Чтобы установить надежную связь, нам нужен качественный вывод. Потери передачи канала и другие факторы, влияющие на качество сигнала, должны быть обработаны. Самая большая потеря, как мы уже говорили, это ISI.

Чтобы сделать сигнал свободным от ISI и обеспечить максимальное отношение сигнал / шум, нам необходимо реализовать метод, называемый эквалайзером . На следующем рисунке показан эквалайзер в приемной части системы связи.

Шум и помехи, обозначенные на рисунке, могут возникать во время передачи. Регенеративный повторитель имеет схему эквалайзера, которая компенсирует потери при передаче, формируя схему. Эквалайзер можно реализовать.

Вероятность ошибки и показатель качества

Скорость передачи данных называется скоростью передачи данных . Скорость, с которой возникает ошибка в битах, при передаче данных называется частотой ошибок по битам (BER) .

Вероятность появления BER — это вероятность ошибки . Увеличение отношения сигнал / шум (SNR) уменьшает BER, следовательно, вероятность ошибки также уменьшается.

В аналоговом приемнике показатель качества в процессе обнаружения можно назвать отношением выходного SNR к входному SNR. Большим достоинством будет преимущество.

Методы цифровой модуляции

Цифро-аналоговые сигналы — это следующее преобразование, которое мы обсудим в этой главе. Эти методы также называются методами цифровой модуляции .

Цифровая модуляция обеспечивает большую информационную емкость, высокую безопасность данных, быструю доступность системы и отличное качество связи. Следовательно, методы цифровой модуляции имеют большую потребность в их способности передавать большие объемы данных, чем методы аналоговой модуляции.

Существует много типов методов цифровой модуляции, а также их комбинации, в зависимости от необходимости. Из них все мы обсудим выдающиеся.

ASK — Amplitude Shift Keying

Амплитуда результирующего выходного сигнала зависит от входных данных, должен ли он быть нулевым уровнем или изменением положительного и отрицательного в зависимости от несущей частоты.

FSK — частотная манипуляция

Частота выходного сигнала будет высокой или низкой, в зависимости от применяемых входных данных.

PSK — Фазовая манипуляция

Фаза выходного сигнала смещается в зависимости от входа. В основном это два типа, а именно двоичная фазовая манипуляция (BPSK) и квадратурная фазовая манипуляция (QPSK), в зависимости от количества фазовых сдвигов. Другой — это дифференциальная фазовая манипуляция (DPSK), которая изменяет фазу в соответствии с предыдущим значением.

M-арное кодирование

Методы M-арного кодирования — это методы, в которых для передачи одновременно по одному сигналу создается более двух битов. Это помогает в уменьшении пропускной способности.

Типы М-арных техник —

• M-арый ASK
• М-арый ФСК
• М-арый ПСК

Все это обсуждается в последующих главах.

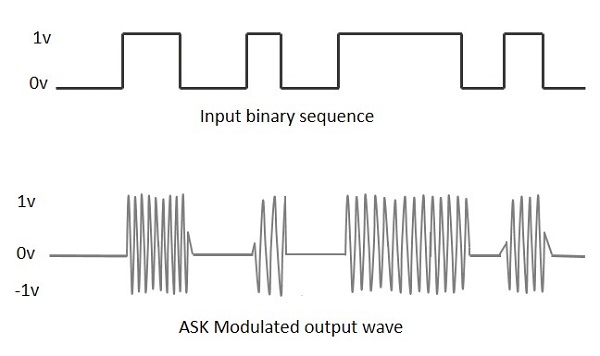
Переключение амплитуды

Amplitude Shift Keying (ASK) — это тип амплитудной модуляции, который представляет двоичные данные в форме изменений амплитуды сигнала.

Любой модулированный сигнал имеет высокочастотную несущую. Двоичный сигнал, когда модулируется ASK, дает нулевое значение для низкого входа, в то время как он дает выход несущей для высокого входа.

На следующем рисунке представлен ASK-модулированный сигнал вместе с его входом.

Чтобы найти процесс получения этой ASK-модулированной волны, давайте узнаем о работе модулятора ASK.

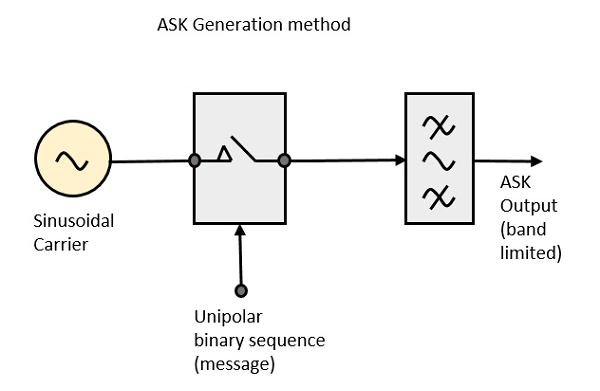
ASK Модулятор

Блок-схема модулятора ASK состоит из генератора несущего сигнала, двоичной последовательности из сигнала сообщения и фильтра с ограниченной полосой частот. Ниже приведена блок-схема модулятора ASK.

Генератор несущих, посылает непрерывную высокочастотную несущую. Бинарная последовательность из сигнала сообщения делает униполярный вход высоким или низким. Высокий сигнал замыкает переключатель, позволяя несущей волне. Следовательно, на выходе будет сигнал несущей на высоком входе. При низком входе переключатель размыкается, и напряжение не появляется. Следовательно, выход будет низким.

Фильтр ограничения полосы формирует импульс в зависимости от амплитудных и фазовых характеристик фильтра ограничения полосы или фильтра формирования импульса.

АСК Демодулятор

Существует два типа методов демодуляции ASK. Они —

• Асинхронная ASK Демодуляция / обнаружение
• Синхронный ASK Демодуляция / обнаружение

Тактовая частота на передатчике, когда она совпадает с тактовой частотой на приемнике, известна как синхронный метод , поскольку частота синхронизируется. В противном случае он известен как асинхронный .

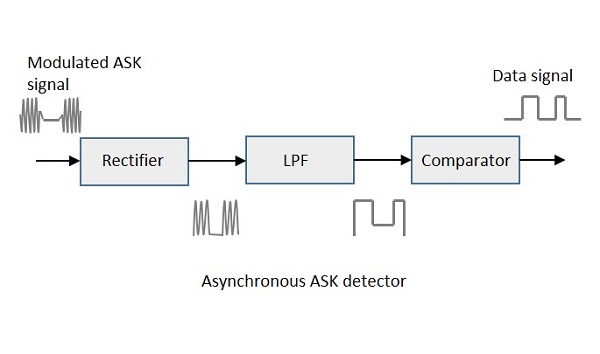
Асинхронный демодулятор ASK

Асинхронный детектор ASK состоит из полуволнового выпрямителя, фильтра низких частот и компаратора. Ниже приведена блок-схема для того же.

Модулированный сигнал ASK поступает на полуволновой выпрямитель, который выдает положительную половину выходного сигнала. Фильтр нижних частот подавляет более высокие частоты и дает выходной сигнал с обнаруженной огибающей, с которого компаратор выдает цифровой выход.

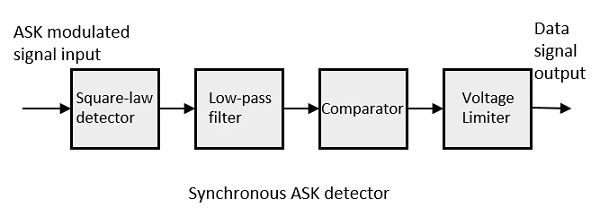
Синхронный демодулятор ASK

Синхронный детектор ASK состоит из детектора квадратичного закона, фильтра низких частот, компаратора и ограничителя напряжения. Ниже приведена блок-схема для того же.

Модулированный входной сигнал ASK подается на детектор квадратичного закона. Квадратный детектор — это детектор, выходное напряжение которого пропорционально квадрату амплитудно-модулированного входного напряжения. Фильтр нижних частот минимизирует более высокие частоты. Компаратор и ограничитель напряжения помогают получить чистый цифровой выход.

Переключение частот

Управление сдвигом частоты (FSK) — это метод цифровой модуляции, в котором частота несущего сигнала изменяется в соответствии с изменениями цифрового сигнала. ФСК представляет собой схему частотной модуляции.

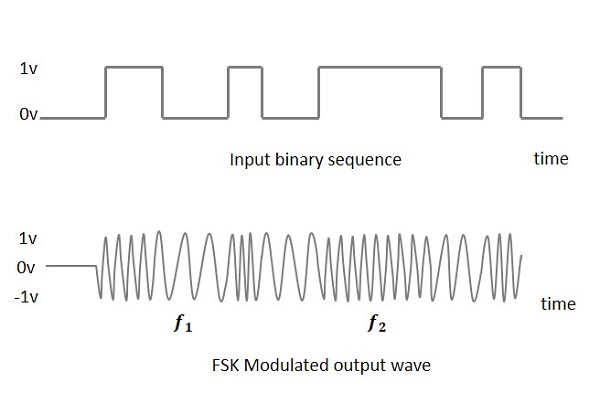
Выход модулированной волны FSK имеет высокую частоту для двоичного входа High и низкую частоту для двоичного входа Low. Двоичные 1 и 0 называются частотами Марка и Космоса.

Следующее изображение является схематическим представлением модулированного сигнала FSK вместе с его входом.

Чтобы найти процесс получения этой FSK-модулированной волны, сообщите нам о работе FSK-модулятора.

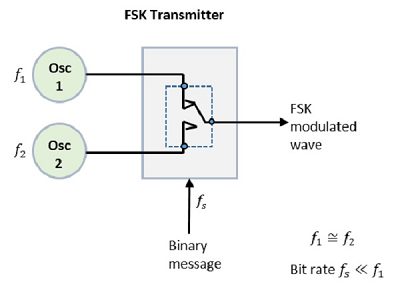
ФСК Модулятор

Блок-схема модулятора FSK состоит из двух генераторов с тактовой частотой и входной двоичной последовательности. Ниже приведена блок-схема.

Два генератора, генерирующие сигналы более высокой и более низкой частоты, подключаются к переключателю вместе с внутренним тактовым сигналом. Чтобы избежать резких скачков фазы выходного сигнала во время передачи сообщения, тактовые импульсы применяются к обоим генераторам внутри. Последовательность двоичных входов применяется к передатчику для выбора частот в соответствии с двоичным входом.

ФСК Демодулятор

Существуют разные методы демодуляции волны FSK. Основными методами обнаружения FSK являются асинхронный детектор и синхронный детектор . Синхронный детектор является когерентным, а асинхронный детектор — некогерентным.

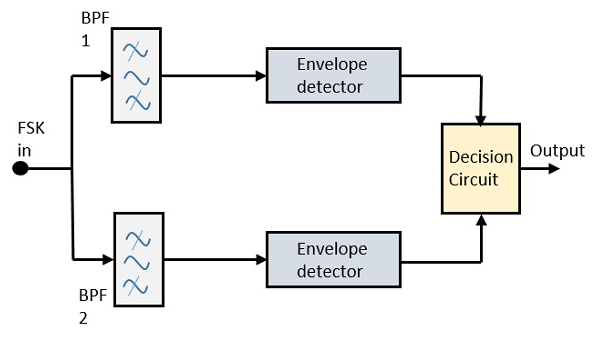
Асинхронный детектор FSK

Блок-схема асинхронного детектора FSK состоит из двух полосовых фильтров, двух детекторов огибающей и схемы принятия решения. Ниже приведено схематическое изображение.

Сигнал FSK пропускается через два полосовых фильтра (BPF), настроенных на частоты Space и Mark . Выходные данные от этих двух BPF выглядят как сигнал ASK, который подается на детектор огибающей. Сигнал в каждом детекторе огибающей модулируется асинхронно.

Схема принятия решения выбирает, какой выход более вероятен, и выбирает его из любого из детекторов огибающей. Это также изменяет форму волны до прямоугольной.

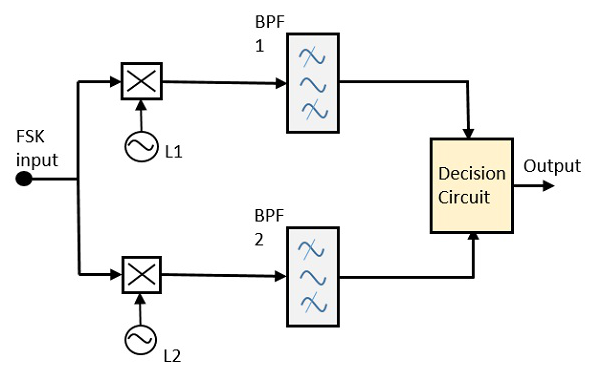
Синхронный детектор FSK

Блок-схема Синхронного детектора FSK состоит из двух смесителей с цепями гетеродина, двух полосовых фильтров и схемы принятия решения. Ниже приведено схематическое изображение.

Входной сигнал FSK подается на два смесителя с цепями гетеродина. Эти два связаны с двумя полосовыми фильтрами. Эти комбинации действуют как демодуляторы, и схема принятия решения выбирает, какой выход более вероятен, и выбирает его из любого из детекторов. Два сигнала имеют минимальное частотное разделение.

Для обоих демодуляторов полоса пропускания каждого из них зависит от их битрейта. Этот синхронный демодулятор немного сложнее, чем демодуляторы асинхронного типа.

Цифровая связь — фазовая манипуляция

Фазовая манипуляция (PSK) — это метод цифровой модуляции, при котором фаза несущего сигнала изменяется путем изменения синусоидальных и косинусных входов в конкретное время. Техника PSK широко используется для беспроводных локальных сетей, биометрических, бесконтактных операций, а также для связи RFID и Bluetooth.

PSK бывает двух типов, в зависимости от фаз, на которые сдвигается сигнал. Они —

Бинарная фазовая манипуляция (BPSK)

Это также называется 2-фазной PSK или фазовой манипуляцией. В этом методе несущая синусоидальной волны принимает два обращения фазы, такие как 0 ° и 180 °.

BPSK — это, по сути, схема модуляции с двухполосной подавленной несущей (DSBSC), поскольку сообщение является цифровой информацией.

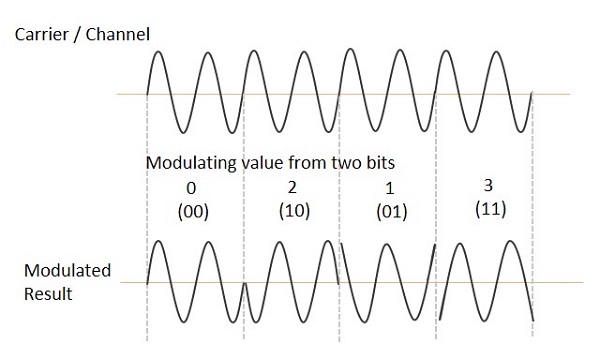
Квадратурная фазовая манипуляция (QPSK)

Это метод фазовой манипуляции, при котором несущая синусоидальной волны принимает четыре фазовых реверса, таких как 0 °, 90 °, 180 ° и 270 °.

Если этот вид методов еще более расширен, PSK также может быть выполнен с восемью или шестнадцатью значениями, в зависимости от требования.

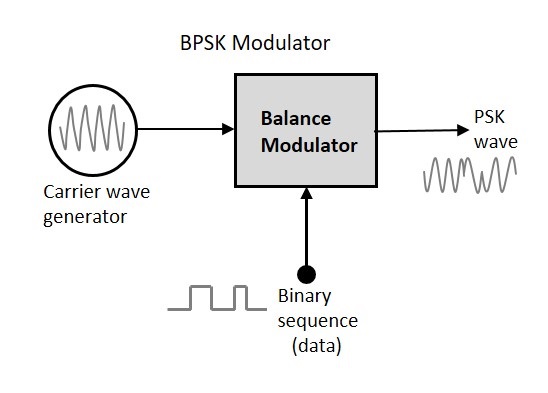
БПСК Модулятор

Блок-схема двоичной фазовой манипуляции состоит из модулятора баланса, в котором синусоида несущей является одним входом, а двоичная последовательность — другим входом. Ниже приведено схематическое изображение.

Модуляция BPSK выполняется с использованием модулятора баланса, который умножает два сигнала, подаваемых на вход. Для нулевого двоичного входа фаза будет 0 °, а для высокого входа, фазовое обращение составляет 180 ° .

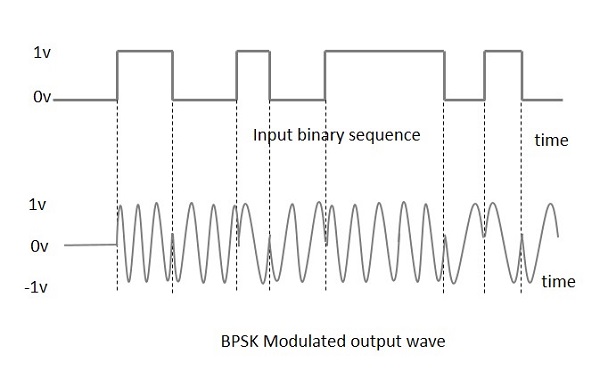
Ниже приведено схематическое представление BPSK модулированной выходной волны вместе с ее заданным входом.

Выходная синусоидальная волна модулятора будет являться носителем прямого ввода или инвертированной (с фазовым сдвигом 180) входной несущей, которая является функцией сигнала данных.

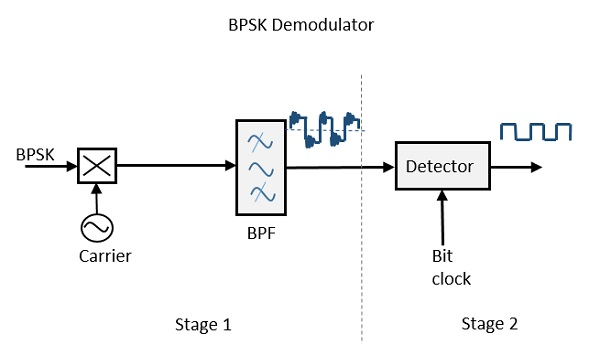
БПСК Демодулятор

Блок-схема демодулятора BPSK состоит из смесителя с цепью гетеродина, полосового фильтра, схемы входа с двумя входами. Диаграмма выглядит следующим образом.

При восстановлении сигнала сообщения с ограниченной полосой пропускания с помощью микшерной схемы и полосового фильтра завершается первый этап демодуляции. Получается сигнал основной полосы частот, который ограничен полосой, и этот сигнал используется для восстановления потока двоичных сообщений.

На следующем этапе демодуляции в схеме детектора требуется тактовая частота в битах для создания исходного двоичного сигнала сообщения. Если скорость передачи в битах кратна несущей частоте, то регенерация тактовой частоты в битах упрощается. Чтобы сделать схему легко понятной, схема принятия решения также может быть вставлена ​​на 2- ^й стадии обнаружения.

Квадратурная фазовая манипуляция

Квадратурная фазовая манипуляция (QPSK) является разновидностью BPSK, и это также схема модуляции с двухполосной подавленной несущей (DSBSC), которая отправляет два бита цифровой информации за один раз, называемые bigits .

Вместо преобразования цифровых битов в серию цифровых потоков он преобразует их в битовые пары. Это уменьшает скорость передачи данных до половины, что позволяет пространство для других пользователей.

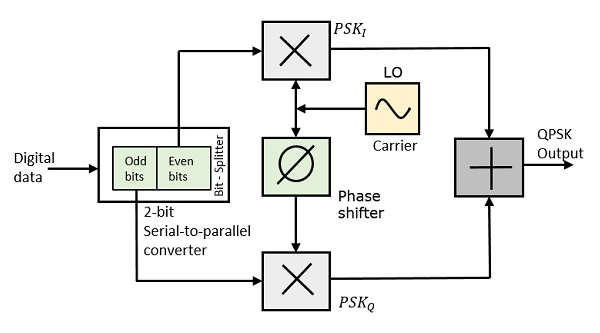
QPSK Модулятор

Модулятор QPSK использует разделитель битов, два умножителя с локальным генератором, 2-разрядный преобразователь последовательный в параллельный и летнюю схему. Ниже приведена блок-схема для того же.

На входе модулятора четные биты сигнала сообщения (т. Е. 2- ^й бит, 4- ^й бит, 6- ^й бит и т. Д.) И нечетные биты (т. Е. 1-й бит, 3- ^й бит, 5- ^й бит и т. Д.) Разделяются делителем битов и умножаются на одну и ту же несущую для генерации нечетного BPSK (называемого PSK _I ) и четного BPSK (называемого PSK _Q ). _Q- сигнал PSK в любом случае сдвигается по фазе на 90 °, а затем модулируется.

Форма сигнала QPSK для двухбитового входа выглядит следующим образом, который показывает модулированный результат для разных экземпляров двоичных входов.

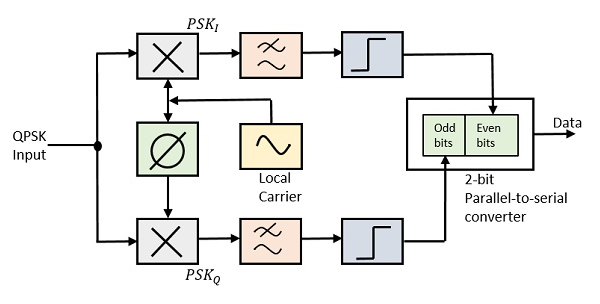
QPSK Демодулятор

В демодуляторе QPSK используются две схемы демодулятора продукта с локальным генератором, два полосовых фильтра, две схемы интегратора и 2-разрядный параллельный преобразователь в последовательный. Ниже приведена схема для того же.

Два детектора продукта на входе демодулятора одновременно демодулируют два сигнала BPSK. Пара битов восстановлена ​​здесь из исходных данных. Эти сигналы после обработки передаются в параллельно-последовательный преобразователь.

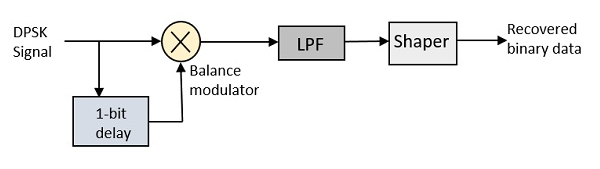
Дифференциальная фазовая манипуляция

В дифференциальной фазовой манипуляции (DPSK) фаза модулированного сигнала сдвигается относительно предыдущего элемента сигнала. Опорный сигнал здесь не рассматривается. Фаза сигнала следует за высоким или низким состоянием предыдущего элемента. Этот метод ДФМ не нужен опорный генератор.

На следующем рисунке представлена ​​модель формы волны DPSK.

Из вышеприведенного рисунка видно, что если бит данных имеет низкий уровень, т. Е. 0, то фаза сигнала не инвертируется, а продолжается, как и была. Если данные имеют высокое значение, т. Е. 1, то фаза сигнала инвертируется, как в случае NRZI, инвертируется в 1 (форма дифференциального кодирования).

Если мы наблюдаем вышеуказанную форму волны, мы можем сказать, что состояние High представляет M в модулирующем сигнале, а состояние Low представляет W в модулирующем сигнале.

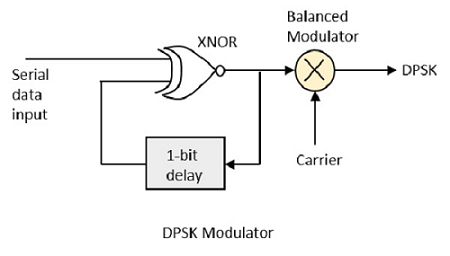
DPSK Модулятор

DPSK — это метод BPSK, в котором отсутствует опорный фазовый сигнал. Здесь, сам передаваемый сигнал может быть использован в качестве опорного сигнала. Ниже приведена схема модулятора DPSK.

DPSK кодирует два разных сигнала, то есть несущую и модулирующий сигнал с фазовым сдвигом 180 ° каждый. Последовательный ввод данных передается на вентиль XNOR, а выход снова возвращается на другой вход с 1-битной задержкой. Выходной сигнал затвора XNOR вместе с сигналом несущей передается в модулятор баланса, чтобы получить модулированный сигнал DPSK.

DPSK Демодулятор

В демодуляторе DPSK фаза обращенного бита сравнивается с фазой предыдущего бита. Ниже приведена блок-схема демодулятора DPSK.

Из приведенного выше рисунка видно, что модулятор баланса получает сигнал DPSK вместе с 1-битным входом задержки. Этот сигнал сделан, чтобы ограничиться более низкими частотами с помощью ФНЧ. Затем он передается в схему формирователя, которая является компаратором или схемой триггера Шмитта, для восстановления исходных двоичных данных в качестве выходных данных.

Цифровая связь — M-арное кодирование

Слово двоичное представляет два бита. М представляет собой цифру, которая соответствует числу условий, уровней или комбинаций, возможных для данного числа двоичных переменных.

Это тип техники цифровой модуляции, используемой для передачи данных, в которой вместо одного бита одновременно передаются два или более бита. Поскольку для передачи нескольких битов используется один сигнал, ширина полосы канала уменьшается.

M-арное уравнение

Если цифровой сигнал подается при четырех условиях, таких как уровни напряжения, частоты, фазы и амплитуда, то M = 4 .

Количество битов, необходимых для получения заданного количества условий, математически выражается как

$$N = \ log_ {2} {M}$$

куда

N — количество необходимых бит

M — количество условий, уровней или комбинаций, возможных с N битами.

Вышеупомянутое уравнение может быть перестроено как

$$2 ^ N = M$$

Например, с двумя битами возможно 2 ² = 4 условия.

Типы M-арных техник

В общем, многоуровневые (M-арные) методы модуляции используются в цифровой связи, так как на входе передатчика разрешены цифровые входы с более чем двумя уровнями модуляции. Следовательно, эти методы являются эффективными по полосе пропускания.

Есть много M-арных методов модуляции. Некоторые из этих методов модулируют один параметр сигнала несущей, такой как амплитуда, фаза и частота.

M-арый ASK

Это называется M-арной амплитудной манипуляцией (M-ASK) или M-арной амплитудно-импульсной модуляцией (PAM).

Амплитуда сигнала несущей, принимает М разных уровней.

Представительство М-арой АСК

Sm(t)=Amcos(2 pifct) quadAm epsilon(2m−1−M) Delta,m=1,2....M quadи quad0 leqt leqTs$S_m (t) = A_mcos (2 \ pi f_ct) \ quad A_m \ epsilon {(2m - 1 - M) \ Delta, m = 1,2 ... \: .M} \ quad и \ quad 0 \ leq t \ leq T_s$

Некоторые характерные особенности M-ary ASK —

• Этот метод также используется в PAM.
• Его реализация проста.
• M-арый ASK подвержен шуму и искажениям.

М-арый ФСК

Это называется M-арной частотной манипуляцией (M-арный FSK).

Частота несущего сигнала принимает М разных уровней.

Представительство М-арый ФСК

$S_i (t) = \ sqrt {\ frac {2E_s} {T_s}} \ cos \ left (\ frac {\ pi} {T_s} \ left (n_c + i \ right) t \ right)$ 0 leqt leqTs quadи quadi=1,2,3.....M$0 \ leq t \ leq T_s \ quad и \ quad i = 1,2,3 ... \: ..M$

Где $f_c = \ frac {n_c} {2T_s}$ для некоторого фиксированного целого числа n.

Некоторые характерные черты M-ary FSK —

• Не подвержен шуму так сильно, как ASK.

• Количество передаваемых М сигналов равно по энергии и длительности.

• Сигналы разделены $\ frac {1} {2T_s}$ Гц, что делает сигналы ортогональными друг другу.

• Поскольку М сигналов являются ортогональными, в пространстве сигналов нет скученности.

• Эффективность полосы пропускания M-арного FSK уменьшается, а КПД мощности увеличивается с увеличением M.

Не подвержен шуму так сильно, как ASK.

Количество передаваемых М сигналов равно по энергии и длительности.

Сигналы разделены $\ frac {1} {2T_s}$ Гц, что делает сигналы ортогональными друг другу.

Поскольку М сигналов являются ортогональными, в пространстве сигналов нет скученности.

Эффективность полосы пропускания M-арного FSK уменьшается, а КПД мощности увеличивается с увеличением M.

М-арый ПСК

Это называется M-арной фазовой манипуляцией (M-арный PSK).

Фаза несущего сигнала принимает М разных уровней.

Представительство М-арый ПСК

$S_i (t) = \ sqrt {\ frac {2E} {T}} \ cos \ left (w_o t + \ phi _it \ right)$ $0 \ leq t \ leq T \ quad и \ quad i = 1,2 ... M$

 phii left(t right)= frac2 piiM quadгде quadi=1,2,3......M $$\ phi _i \ left (t \ right) = \ frac {2 \ pi i} {M} \ quad где \ quad i = 1,2,3 ... \: ... M$$

Некоторые характерные особенности M-ary PSK —

• Конверт является постоянным с большим количеством фазовых возможностей.

• Этот метод использовался в первые дни космической связи.

• Лучшая производительность, чем у ASK и FSK.

• Минимальная ошибка оценки фазы на приемнике.

• Эффективность полосы пропускания M-ary PSK уменьшается, а КПД мощности увеличивается с увеличением M.

Конверт является постоянным с большим количеством фазовых возможностей.

Этот метод использовался в первые дни космической связи.

Лучшая производительность, чем у ASK и FSK.

Минимальная ошибка оценки фазы на приемнике.

Эффективность полосы пропускания M-ary PSK уменьшается, а КПД мощности увеличивается с увеличением M.

До сих пор мы обсуждали различные методы модуляции. Результатом всех этих методов является двоичная последовательность, представленная как 1 и 0 . Эта двоичная или цифровая информация имеет много типов и форм, которые обсуждаются далее.

Цифровая связь — теория информации

Информация является источником системы связи, будь то аналоговая или цифровая. Теория информации — это математический подход к изучению кодирования информации наряду с количественным определением, хранением и передачей информации.

Условия возникновения событий

Если мы рассмотрим событие, есть три условия возникновения.

• Если событие не произошло, возникает условие неопределенности .

• Если событие только что произошло, возникает условие неожиданности .

• Если событие произошло, время назад, есть условие наличия некоторой информации .

Если событие не произошло, возникает условие неопределенности .

Если событие только что произошло, возникает условие неожиданности .

Если событие произошло, время назад, есть условие наличия некоторой информации .

Эти три события происходят в разное время. Разница в этих условиях помогает нам получить знания о вероятности возникновения событий.

Энтропия

Когда мы наблюдаем возможности возникновения события, насколько удивительным или неопределенным оно было бы, это означает, что мы пытаемся получить представление о среднем содержании информации из источника события.

Энтропия может быть определена как мера среднего информационного содержания на исходный символ. Клод Шеннон , «отец теории информации», сформулировал для нее формулу:

$$H = - \ sum_ {i} p_i \ log_ {b} p_i$$

Где p _i — вероятность появления символа i из заданного потока символов, а b — основа используемого алгоритма. Следовательно, это также называется энтропией Шеннона .

Величина неопределенности, оставшаяся относительно входа канала после наблюдения за выходом канала, называется условной энтропией . Обозначается $H (x \ mid y)$

Взаимная информация

Давайте рассмотрим канал с выходом Y и входом X

Пусть энтропия для предыдущей неопределенности будет X = H (x)

(Предполагается, что перед вводом применяется)

Чтобы узнать о неопределенности выходных данных, после применения входных данных рассмотрим условную энтропию, учитывая, что Y = y _k

$$H \ left (x \ mid y_k \ right) = \ sum_ {j = 0} ^ {j - 1} p \ left (x_j \ mid y_k \ right) \ log_ {2} \ left [\ frac {1 } {p (x_j \ mid y_k)} \ right]$$

Это случайная величина для H(X midy=y0)...............H(X midy=yk)$H (X \ mid y = y_0) \: ... \: ... \: ... \: ... \: ... \: H (X \ mid y = y_k)$ с вероятностями p(y0)............p(yk−1)$p (y_0) \: ... \: ... \: ... \: ... \: p (y_ {k-1)}$ соответственно.

Среднее значение $H (X \ mid y = y_k)$ для выходного алфавита y равно —

$H \ left (X \ mid Y \ right) = \ displaystyle \ sum \ limit_ {k = 0} ^ {k - 1} H \ left (X \ mid y = y_k \ right) p \ left (y_k \ right) )$

$= \ displaystyle \ sum \ limit_ {k = 0} ^ {k - 1} \ displaystyle \ sum \ limit_ {j = 0} ^ {j - 1} p \ left (x_j \ mid y_k \ right) p \ left (y_k \ right) \ log_ {2} \ left [\ frac {1} {p \ left (x_j \ mid y_k \ right)} \ right]$

$= \ displaystyle \ sum \ limit_ {k = 0} ^ {k - 1} \ displaystyle \ sum \ limit_ {j = 0} ^ {j - 1} p \ left (x_j, y_k \ right) \ log_ {2 } \ left [\ frac {1} {p \ left (x_j \ mid y_k \ right)} \ right]$

Теперь, учитывая оба условия неопределенности (до и после применения входных данных), мы узнаем, что разница, то есть $H (x) - H (x \ mid y)$, должна представлять неопределенность относительно разрешенного входа канала наблюдая за выходом канала.

Это называется Взаимной Информацией канала.

Обозначая взаимную информацию как $I (x; y)$, мы можем записать все это в уравнении следующим образом

$$I (x; y) = H (x) - H (x \ mid y)$$

Следовательно, это уравновешенное представление Взаимной Информации.

Свойства Взаимной информации

Это свойства Взаимной информации.

• Взаимная информация канала симметрична.

  $$I (x; y) = I (y; x)$$

• Взаимная информация неотрицательна.

  $$I (x; y) \ geq 0$$

• Взаимная информация может быть выражена в терминах энтропии выхода канала.

  $$I (x; y) = H (y) - H (y \ mid x)$$

  Где $H (y \ mid x)$ — условная энтропия

• Взаимная информация о канале связана с совместной энтропией входа канала и выхода канала.

  $$I (x; y) = H (x) + H (y) - H (x, y)$$

  Где совместная энтропия $H (x, y)$ определяется как

  $$H (x, y) = \ displaystyle \ sum \ limit_ {j = 0} ^ {j-1} \ displaystyle \ sum \ limit_ {k = 0} ^ {k-1} p (x_j, y_k) \ log_ {2} \ left (\ frac {1} {p \ left (x_i, y_k \ right)} \ right)$$

Взаимная информация канала симметрична.

$$I (x; y) = I (y; x)$$

Взаимная информация неотрицательна.

$$I (x; y) \ geq 0$$

Взаимная информация может быть выражена в терминах энтропии выхода канала.

$$I (x; y) = H (y) - H (y \ mid x)$$

Где $H (y \ mid x)$ — условная энтропия

Взаимная информация о канале связана с совместной энтропией входа канала и выхода канала.

$$I (x; y) = H (x) + H (y) - H (x, y)$$

Где совместная энтропия $H (x, y)$ определяется как

$$H (x, y) = \ displaystyle \ sum \ limit_ {j = 0} ^ {j-1} \ displaystyle \ sum \ limit_ {k = 0} ^ {k-1} p (x_j, y_k) \ log_ {2} \ left (\ frac {1} {p \ left (x_i, y_k \ right)} \ right)$$

Емкость канала

Мы до сих пор обсуждали взаимную информацию. Максимальная средняя взаимная информация в момент интервала сигнализации при передаче по дискретному каналу без памяти, вероятности скорости максимально надежной передачи данных, может пониматься как пропускная способность канала .

Он обозначается буквой C и измеряется в битах на канал .

Дискретный источник без памяти

Источник, из которого данные передаются через последовательные интервалы, который не зависит от предыдущих значений, можно назвать дискретным источником без памяти .

Этот источник является дискретным, поскольку он рассматривается не для непрерывного временного интервала, а для дискретных временных интервалов. Этот источник не имеет памяти, так как он свеж в каждый момент времени, без учета предыдущих значений.

Теорема об исходном кодировании

Код, созданный из дискретного источника без памяти, должен быть эффективно представлен, что является важной проблемой в коммуникации. Для этого существуют кодовые слова, которые представляют эти исходные коды.

Например, в телеграфии мы используем азбуку Морзе, в которой алфавиты обозначаются знаками и пробелами . Если рассматривается буква E , которая в основном используется, она обозначается как «.», Тогда как буква Q, которая используется редко, обозначается как «—.-»

Давайте посмотрим на блок-схему.

Где S _k — это выход дискретного источника без памяти, а b _k — это выход исходного кодера, который представлен 0 и 1 .

Кодированная последовательность такова, что она удобно декодируется в приемнике.

Предположим, что источник имеет алфавит с k различными символами и что k- ^й символ S _k встречается с вероятностью P _k , где k = 0, 1… k-1 .

Пусть двоичное кодовое слово, присвоенное символу S _k кодером, имеющим длину l _k , измеряется в битах.

Следовательно, мы определяем среднюю длину L кодового слова исходного кодера как

$$\ overline {L} = \ displaystyle \ sum \ limit_ {k = 0} ^ {k-1} p_kl_k$$

L представляет среднее количество битов на исходный символ

Если Lmin=минимумвозможнозначениеof overlineL$L_ {min} = \: минимум \: возможно \: значение \: of \: \ overline {L}$

Тогда эффективность кодирования может быть определена как

$$\ eta = \ frac {L {min}} {\ overline {L}}$$

С $\ overline {L} \ geq L_ {min}$ у нас будет $\ eta \ leq 1$

Тем не менее, исходный кодер считается эффективным, когда $\ eta = 1$

Для этого необходимо определить значение $L_ {min}$.

Обратимся к определению: «Для дискретного источника энтропии $H (\ delta)$ без памяти средняя длина кодового слова L для любой исходной кодировки ограничена как $\ overline {L} \ geq H (\ delta)$ «.

Проще говоря, кодовое слово (например: азбука Морзе для слова QUEUE — это -.- ..-. ..-.) Всегда больше или равно исходному коду (в примере QUEUE). Это означает, что символы в кодовом слове больше или равны алфавиту в исходном коде.

Следовательно, при $L_ {min} = H (\ delta)$ эффективность исходного кодера в терминах энтропии $H (\ delta)$ может быть записана как

$$\ eta = \ frac {H (\ delta)} {\ overline {L}}$$

Эта теорема кодирования источника называется теоремой кодирования без помех, поскольку она устанавливает кодирование без ошибок. Это также называется первой теоремой Шеннона .

Теорема о канальном кодировании

Шум, присутствующий в канале, создает нежелательные ошибки между входной и выходной последовательностями цифровой системы связи. Вероятность ошибки должна быть очень низкой, около ≤ 10 ^-6 для надежной связи.

Канальное кодирование в системе связи вводит избыточность с управлением, чтобы повысить надежность системы. Исходное кодирование уменьшает избыточность для повышения эффективности системы.

Канальное кодирование состоит из двух частей действия.

• Отображение последовательности входящих данных в последовательность ввода канала.

• Обратное отображение выходной последовательности канала в выходную последовательность данных.

Отображение последовательности входящих данных в последовательность ввода канала.

Обратное отображение выходной последовательности канала в выходную последовательность данных.

Конечная цель состоит в том, чтобы общее влияние шума канала было минимизировано.

Отображение выполняется передатчиком с помощью кодера, тогда как обратное отображение выполняется декодером в приемнике.

Канальное кодирование

Рассмотрим дискретный канал без памяти (δ) с энтропией H (δ).

T _s указывает символы, которые δ дает в секунду

Емкость канала обозначена буквой C

Канал может быть использован для каждой T _c секунд

Следовательно, максимальная пропускная способность канала равна C / T _c.

Отправленные данные = $\ frac {H (\ delta)} {T_s}$

Если $\ frac {H (\ delta)} {T_s} \ leq \ frac {C} {T_c}$, это означает, что передача хороша и может быть воспроизведена с небольшой вероятностью ошибки.

В этом случае $\ frac {C} {T_c}$ является критической скоростью пропускной способности канала.

Если $\ frac {H (\ delta)} {T_s} = \ frac {C} {T_c}$, то говорят, что система сигнализирует с критической скоростью.

И наоборот, если $\ frac {H (\ delta)} {T_s}> \ frac {C} {T_c}$, передача невозможна.

Следовательно, максимальная скорость передачи равна критической скорости пропускной способности канала для надежных безошибочных сообщений, которые могут иметь место, по дискретному каналу без памяти. Это называется теоремой канального кодирования .

Цифровая связь — код контроля ошибок

Шум или ошибка — основная проблема в сигнале, которая нарушает надежность системы связи. Кодирование с контролем ошибок — это процедура кодирования, выполняемая для контроля появления ошибок. Эти методы помогают в обнаружении ошибок и исправлении ошибок.

Существует много различных кодов, исправляющих ошибки, в зависимости от применяемых к ним математических принципов. Но исторически эти коды были классифицированы на линейные блочные коды и коды свертки .

Линейные Блочные Коды

В линейных блочных кодах биты четности и биты сообщения имеют линейную комбинацию, что означает, что результирующее кодовое слово является линейной комбинацией любых двух кодовых слов.

Рассмотрим некоторые блоки данных, которые содержат k битов в каждом блоке. Эти биты отображаются с блоками, которые имеют n битов в каждом блоке. Здесь n больше, чем k . Передатчик добавляет избыточные биты, которые являются (nk) битами. Отношение k / n является скоростью кода . Обозначается через r, а значение r равно r <1 .

Добавленные здесь биты (nk) являются битами четности . Биты четности помогают в обнаружении и исправлении ошибок, а также в поиске данных. В передаваемых данных самые левые биты кодового слова соответствуют битам сообщения, а самые правые биты кодового слова соответствуют битам четности.

Систематический код

Любой линейный блочный код может быть систематическим кодом, пока он не будет изменен. Следовательно, неизмененный блочный код называется систематическим кодом .

Ниже приведено представление структуры кодовых слов в соответствии с их распределением.

Если сообщение не изменено, оно называется систематическим кодом. Это означает, что шифрование данных не должно изменять данные.

Сверточные коды

До сих пор в линейных кодах мы обсуждали, что систематический неизмененный код является предпочтительным. Здесь данные из общего числа n битов, если переданы, k битов являются битами сообщения и (nk) битами являются биты четности.

В процессе кодирования биты четности вычитаются из целых данных, а биты сообщения кодируются. Теперь биты четности снова добавляются, и все данные снова кодируются.

На следующем рисунке приведены примеры блоков данных и потоков данных, используемых для передачи информации.

Весь процесс, изложенный выше, утомителен и имеет недостатки. Выделение буфера является основной проблемой, когда система занята.

Этот недостаток устраняется в сверточных кодах. Где весь поток данных назначается символам, а затем передается. Поскольку данные представляют собой поток битов, для хранения не требуется буфер.

Коды Хэмминга

Свойство линейности кодового слова состоит в том, что сумма двух кодовых слов также является кодовым словом. Коды Хэмминга — это тип линейных кодов, исправляющих ошибки , которые могут обнаруживать до двухбитовых ошибок или исправлять однобитовые ошибки без обнаружения неисправленных ошибок.

При использовании кодов Хэмминга дополнительные биты четности используются для идентификации ошибки одного бита. Чтобы перейти от одного бита к другому, в данных нужно изменить несколько битов. Такое количество битов можно назвать расстоянием Хэмминга . Если четность имеет расстояние 2, может быть обнаружен однобитовый переворот. Но это не может быть исправлено. Кроме того, любые два бита не могут быть обнаружены.

Тем не менее, код Хэмминга — лучшая процедура, чем обсуждаемые ранее при обнаружении и исправлении ошибок.

Коды BCH

Коды БЧХ названы в честь изобретателей B ose, C haudari и H ocquenghem. Во время разработки кода BCH существует контроль количества символов, которые должны быть исправлены, и, следовательно, возможна множественная битовая коррекция. Коды БЧХ — это мощный метод исправления ошибок.

Для любых натуральных чисел m ≥ 3 и t <2 ^m-1 существует двоичный код BCH. Ниже приведены параметры такого кода.

Длина блока n = 2 ^м -1

Количество проверочных цифр n — k ≤ mt

Минимальное расстояние d _min ≥ 2t + 1

Этот код может называться кодом BCH с коррекцией ошибок .

Циклические коды

Циклическое свойство кодовых слов заключается в том, что любой циклический сдвиг кодового слова также является кодовым словом. Циклические коды следуют этому циклическому свойству.

Для линейного кода C , если каждое кодовое слово, т. Е. C = (C1, C2, …… Cn) из C, имеет циклический сдвиг вправо компонентов, оно становится кодовым словом. Этот сдвиг вправо равен n-1 циклическим сдвигам влево. Следовательно, он инвариантен при любом сдвиге. Таким образом, линейный код C , поскольку он инвариантен при любом сдвиге, можно назвать циклическим кодом .

Циклические коды используются для исправления ошибок. Они в основном используются для исправления двойных ошибок и пакетных ошибок.

Следовательно, это несколько кодов с исправлением ошибок, которые должны быть обнаружены в приемнике. Эти коды предотвращают появление ошибок и нарушают связь. Они также предотвращают прослушивание сигнала нежелательными приемниками. Для этого существует класс методов сигнализации, которые обсуждаются в следующей главе.

Распространение спектра модуляции

Коллективный класс методов сигнализации используется перед передачей сигнала для обеспечения безопасной связи, известной как модуляция с расширенным спектром . Основным преимуществом метода связи с расширенным спектром является предотвращение «помех», будь то преднамеренное или непреднамеренное.

Сигналы, модулированные этими методами, трудно вмешиваться и не могут быть заблокированы. Злоумышленник, не имеющий официального доступа, никогда не сможет взломать их. Следовательно, эти методы используются в военных целях. Эти сигналы с расширенным спектром передаются с низкой плотностью мощности и имеют широкий разброс сигналов.

Псевдошумовая последовательность

Кодированная последовательность 1 и 0 с определенными свойствами автокорреляции, называемая последовательностью кодирования псевдошума , используется в методах расширения спектра. Это последовательность максимальной длины, которая является типом циклического кода.

Узкополосные сигналы и сигналы с расширенным спектром

Как узкополосный, так и расширенный спектр сигналов можно легко понять, наблюдая их частотный спектр, как показано на следующих рисунках.

Узкополосные сигналы

Узкополосные сигналы имеют концентрированный уровень сигнала, как показано на следующем рисунке частотного спектра.

Ниже приведены некоторые из его особенностей —

• Полоса сигналов занимает узкий диапазон частот.
• Плотность мощности высокая.
• Распространение энергии низкое и концентрированное.

Хотя функции хороши, эти сигналы подвержены помехам.

Сигналы распространения спектра

Сигналы с расширенным спектром имеют интенсивность сигнала, распределенную, как показано на следующем рисунке частотного спектра.

Ниже приведены некоторые из его особенностей —

• Полоса сигналов занимает широкий диапазон частот.
• Плотность мощности очень низкая.
• Энергия широко распространена.

Благодаря этим характеристикам сигналы с расширенным спектром обладают высокой устойчивостью к помехам или помехам. Поскольку несколько пользователей могут совместно использовать одну и ту же полосу частот расширенного спектра, не мешая друг другу, это можно назвать методами множественного доступа .

FHSS и DSSS / CDMA

Методы множественного доступа с расширенным спектром используют сигналы, которые имеют ширину полосы пропускания, превышающую минимальную требуемую ширину полосы РЧ.

Они бывают двух типов.

• Спектр со скачкообразной перестройкой частоты (FHSS)
• Спектр с прямой последовательностью (DSSS)

Спектр со скачкообразной перестройкой частоты (FHSS)

Это метод скачкообразной перестройки частоты, при котором пользователи вынуждены изменять частоты использования от одной к другой за определенный промежуток времени, что называется скачкообразной перестройкой частоты . Например, частота была выделена отправителю 1 на определенный период времени. Теперь через некоторое время отправитель 1 переходит на другую частоту, а отправитель 2 использует первую частоту, которая ранее использовалась отправителем 1. Это называется повторным использованием частоты .

Частоты данных переключаются от одной к другой, чтобы обеспечить безопасную передачу. Количество времени, затрачиваемое на каждый скачок частоты, называется временем задержки .

Спектр с прямой последовательностью (DSSS)

Всякий раз, когда пользователь хочет отправить данные, используя эту технику DSSS, каждый бит пользовательских данных умножается на секретный код, называемый кодом чипирования . Этот код чипа является ничем иным, как кодом расширения, который умножается на исходное сообщение и передается. Получатель использует тот же код для извлечения исходного сообщения.

Сравнение между FHSS и DSSS / CDMA

Оба метода с расширенным спектром популярны по своим характеристикам. Чтобы иметь четкое понимание, давайте посмотрим на их сравнения.

FHSS	DSSS / CDMA
Несколько частот используются	Используется одна частота
Трудно найти частоту пользователя в любой момент времени	Пользовательская частота, однажды выделенная, всегда одинакова
Разрешено повторное использование частот	Повторное использование частот не допускается
Отправителю не нужно ждать	Отправитель должен ждать, если спектр занят
Мощность сигнала высокая	Мощность сигнала низкая
Сильнее и проникает сквозь препятствия	Это слабее по сравнению с FHSS
Это никогда не зависит от помех	Это может зависеть от помех
Это дешевле	Это дорого
Это широко используемая техника	Эта техника не часто используется

Преимущества Spread Spectrum

Ниже приведены преимущества расширения спектра —

• Устранение перекрестных помех
• Лучший вывод с целостностью данных
• Уменьшен эффект многолучевого замирания
• Лучшая безопасность
• Снижение шума
• Сосуществование с другими системами
• Большие рабочие расстояния
• Трудно обнаружить
• Не легко демодулировать / декодировать
• Сложно глушить сигналы

Хотя методы с расширенным спектром были первоначально разработаны для военных целей, в настоящее время они широко используются в коммерческих целях.