Цифровая связь — дельта-модуляция

Частота дискретизации сигнала должна быть выше, чем частота Найквиста, чтобы добиться лучшей дискретизации. Если этот интервал дискретизации в дифференциальной ИКМ значительно уменьшается, разность амплитуд между выборками очень мала, как если бы разность составляла 1-битовое квантование , тогда размер шага будет очень малым, то есть Δ (дельта).

Дельта-модуляция

Тип модуляции, где частота дискретизации намного выше и при которой размер шага после квантования имеет меньшее значение, такая модуляция называется дельта-модуляцией .

Особенности дельта-модуляции

Ниже приведены некоторые особенности дельта-модуляции.

• Вход с избыточной дискретизацией используется для полного использования корреляции сигнала.

• Дизайн квантования прост.

• Входная последовательность намного выше, чем скорость Найквиста.

• Качество умеренное.

• Конструкция модулятора и демодулятора проста.

• Лестничная аппроксимация выходного сигнала.

• Размер шага очень мал, т. Е. Δ (дельта).

• Скорость передачи данных может быть выбрана пользователем.

• Это предполагает более простую реализацию.

Вход с избыточной дискретизацией используется для полного использования корреляции сигнала.

Дизайн квантования прост.

Входная последовательность намного выше, чем скорость Найквиста.

Качество умеренное.

Конструкция модулятора и демодулятора проста.

Лестничная аппроксимация выходного сигнала.

Размер шага очень мал, т. Е. Δ (дельта).

Скорость передачи данных может быть выбрана пользователем.

Это предполагает более простую реализацию.

Дельта-модуляция — это упрощенная форма метода DPCM, также рассматриваемая как 1-битная схема DPCM . При уменьшении интервала выборки корреляция сигнала будет выше.

Дельта модулятор

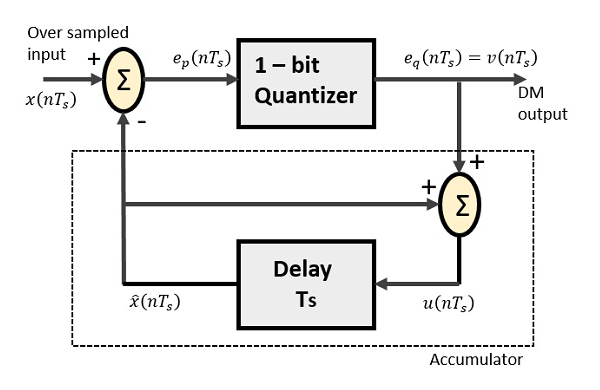
Дельта-модулятор состоит из 1-битного квантователя и цепи задержки, а также двух летних цепей. Ниже приведена блок-схема дельта-модулятора.

Схема предиктора в DPCM заменяется простой схемой задержки в DM.

Из приведенной выше диаграммы мы имеем обозначения как —

• $x (nT_ {s})$ = за выборочный ввод

• $e_ {p} (nT_ {s})$ = летний результат и вход квантователя

• $e_ {q} (nT_ {s})$ = выход квантователя = $v (nT_s)$

• $\ widehat {x} (nT_ {s})$ = выход схемы задержки

• $u (nT_ {s})$ = вход цепи задержки

$x (nT_ {s})$ = за выборочный ввод

$e_ {p} (nT_ {s})$ = летний результат и вход квантователя

$e_ {q} (nT_ {s})$ = выход квантователя = $v (nT_s)$

$\ widehat {x} (nT_ {s})$ = выход схемы задержки

$u (nT_ {s})$ = вход цепи задержки

Используя эти обозначения, теперь мы попытаемся выяснить процесс дельта-модуляции.

$e_ {p} (nT_ {s}) = x (nT_ {s}) - \ widehat {x} (nT_ {s})$

——— уравнение 1

$= x (nT_ {s}) - u ([n - 1] T_ {s})$

$= x (nT_ {s}) - [\ widehat {x} [[n - 1] T_ {s}] + v [[n-1] T_ {s}]]$

——— уравнение 2

В дальнейшем,

$ v (nT_ {s}) = e_ {q} (nT_ {s}) = S.sig. [e_ {p} (nT_ {s})]]

——— уравнение 3

$u (nT_ {s}) = \ widehat {x} (nT_ {s}) + e_ {q} (nT_ {s})$

Куда,

• $\ widehat {x} (nT_ {s})$ = предыдущее значение схемы задержки

• $e_ {q} (nT_ {s})$ = выход квантователя = $v (nT_s)$

$\ widehat {x} (nT_ {s})$ = предыдущее значение схемы задержки

$e_ {q} (nT_ {s})$ = выход квантователя = $v (nT_s)$

Следовательно,

$u (nT_ {s}) = u ([n-1] T_ {s}) + v (nT_ {s})$

——— уравнение 4

Что значит,

Настоящий вход блока задержки

= (Предыдущий выход блока задержки) + (текущий выход квантователя)

Предполагая нулевое условие накопления,

$u (nT_ {s}) = S \ displaystyle \ sum \ limit_ {j = 1} ^ n sig [e_ {p} (jT_ {s})]]$

Накопленная версия вывода DM = $\ displaystyle \ sum \ limit_ {j = 1} ^ nv (jT_ {s})$

——— уравнение 5

Теперь обратите внимание, что

$\ widehat {x} (nT_ {s}) = u ([n-1] T_ {s})$

$= \ displaystyle \ sum \ limit_ {j = 1} ^ {n - 1} v (jT_ {s})$

——— уравнение 6

Выход блока задержки — это отставание выхода Аккумулятора на одну выборку.

Из уравнений 5 и 6 мы получаем возможную структуру для демодулятора.

Аппроксимированная форма волны в лестничной клетке будет выходом дельта-модулятора с размером шага в виде дельты ( Δ ). Качество выходного сигнала умеренное.

Дельта Демодулятор

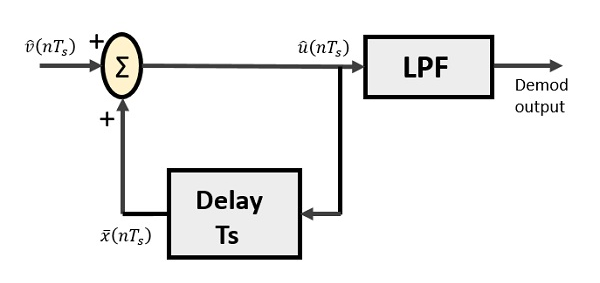
Дельта-демодулятор состоит из фильтра нижних частот, летнего датчика и цепи задержки. Схема предиктора здесь исключена, и, следовательно, предполагаемый вход не поступает на демодулятор.

Ниже приведена схема для дельта-демодулятора.

Из приведенной выше диаграммы мы имеем обозначения как —

• $\ widehat {v} (nT_ {s})$ — входная выборка

• $\ widehat {u} (nT_ {s})$ — летний результат

• $\ bar {x} (nT_ {s})$ — задержанный вывод

$\ widehat {v} (nT_ {s})$ — входная выборка

$\ widehat {u} (nT_ {s})$ — летний результат

$\ bar {x} (nT_ {s})$ — задержанный вывод

Двоичная последовательность будет передана в качестве входа в демодулятор. Примерный выход лестничной клетки дан LPF.

Фильтр нижних частот используется по многим причинам, но основной причиной является устранение шума для внеполосных сигналов. Ошибка размера шага, которая может возникнуть в передатчике, называется зернистым шумом , который здесь исключается. Если шум отсутствует, то выход модулятора равен входу демодулятора.

Преимущества DM над DPCM

• 1-битный квантователь

• Очень легкая конструкция модулятора и демодулятора

1-битный квантователь

Очень легкая конструкция модулятора и демодулятора

Однако в DM существует некоторый шум.

• Искажение наклона при перегрузке (когда Δ мало)

• Зернистый шум (когда Δ велико)

Искажение наклона при перегрузке (когда Δ мало)

Зернистый шум (когда Δ велико)

Адаптивная дельта-модуляция (ADM)

В цифровой модуляции мы столкнулись с определенной проблемой определения размера шага, который влияет на качество выходной волны.

Больший размер шага необходим в крутом наклоне модулирующего сигнала, а меньший размер шага необходим там, где сообщение имеет небольшой наклон. Мельчайшие детали упускаются в процессе. Таким образом, было бы лучше, если бы мы могли регулировать размер шага в соответствии с нашим требованием, чтобы получить выборку желаемым способом. Это концепция адаптивной дельта-модуляции .

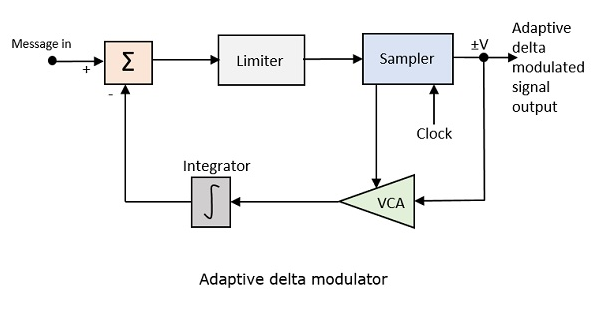
Ниже приведена блок-схема адаптивного дельта-модулятора.

Усиление усилителя, управляемого напряжением, регулируется выходным сигналом сэмплера. Усиление усилителя определяет размер шага, и оба пропорциональны.

ADM квантует разницу между значением текущей выборки и прогнозируемой величиной следующей выборки. Он использует переменную высоту шага для прогнозирования следующих значений для точного воспроизведения быстро меняющихся значений.