Теорема об исходном кодировании

Код, созданный из дискретного источника без памяти, должен быть эффективно представлен, что является важной проблемой в коммуникации. Для этого существуют кодовые слова, которые представляют эти исходные коды.

Например, в телеграфии мы используем азбуку Морзе, в которой алфавиты обозначаются знаками и пробелами . Если рассматривается буква E , которая в основном используется, она обозначается как «.», Тогда как буква Q, которая используется редко, обозначается как «—.-»

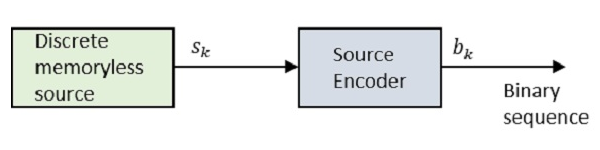
Давайте посмотрим на блок-схему.

Где S _k — это выход дискретного источника без памяти, а b _k — это выход исходного кодера, который представлен 0 и 1 .

Кодированная последовательность такова, что она удобно декодируется в приемнике.

Предположим, что источник имеет алфавит с k различными символами и что k- ^й символ S _k встречается с вероятностью P _k , где k = 0, 1… k-1 .

Пусть двоичное кодовое слово, присвоенное символу S _k кодером, имеющим длину l _k , измеряется в битах.

Следовательно, мы определяем среднюю длину L кодового слова исходного кодера как

 overlineL= displaystyle sum limitk−1k=0pklk

$$\ overline {L} = \ displaystyle \ sum \ limit_ {k = 0} ^ {k-1} p_kl_k$$

L представляет среднее количество битов на исходный символ

Если Lmin=минимумвозможнозначениеof overlineL$L_ {min} = \: минимум \: возможно \: значение \: of \: \ overline {L}$

Тогда эффективность кодирования может быть определена как

 eta= fracLmin overlineL

$$\ eta = \ frac {L {min}} {\ overline {L}}$$

С  overlineL geqLmin$\ overline {L} \ geq L_ {min}$ у нас будет  eta leq1$\ eta \ leq 1$

Тем не менее, исходный кодер считается эффективным, когда  eta=1$\ eta = 1$

Для этого необходимо определить значение Lmin$L_ {min}$.

Обратимся к определению: «Для дискретного источника энтропии H( delta)$H (\ delta)$ без памяти средняя длина кодового слова L для любой исходной кодировки ограничена как  overlineL geqH( delta)$\ overline {L} \ geq H (\ delta)$ «.

Проще говоря, кодовое слово (например: азбука Морзе для слова QUEUE — это -.- ..-. ..-.) Всегда больше или равно исходному коду (в примере QUEUE). Это означает, что символы в кодовом слове больше или равны алфавиту в исходном коде.

Следовательно, при Lmin=H( delta)$L_ {min} = H (\ delta)$ эффективность исходного кодера в терминах энтропии H( delta)$H (\ delta)$ может быть записана как

 eta= fracH( delta) overlineL

$$\ eta = \ frac {H (\ delta)} {\ overline {L}}$$

Эта теорема кодирования источника называется теоремой кодирования без помех, поскольку она устанавливает кодирование без ошибок. Это также называется первой теоремой Шеннона .